October 7, 2024

Convert Binary Tree to Doubly Linked List – Part I

Problem Statement

Given a Binary Tree convert it into a Doubly Linked List (DLL) where the left and right pointers are modified to the previous and next pointers of the resultant Doubly linked list. The order of nodes in the doubly linked list should be the same as the order of the nodes in the Inorder traversal of the binary tree. Therefore the first node(head) of a doubly linked list will be the leftmost node of the binary tree since we are following Inorder traversal.

Example

For a better understanding of the problem statement, let’s look at the below example:

Input:

Consider the input binary tree shown in the below image:

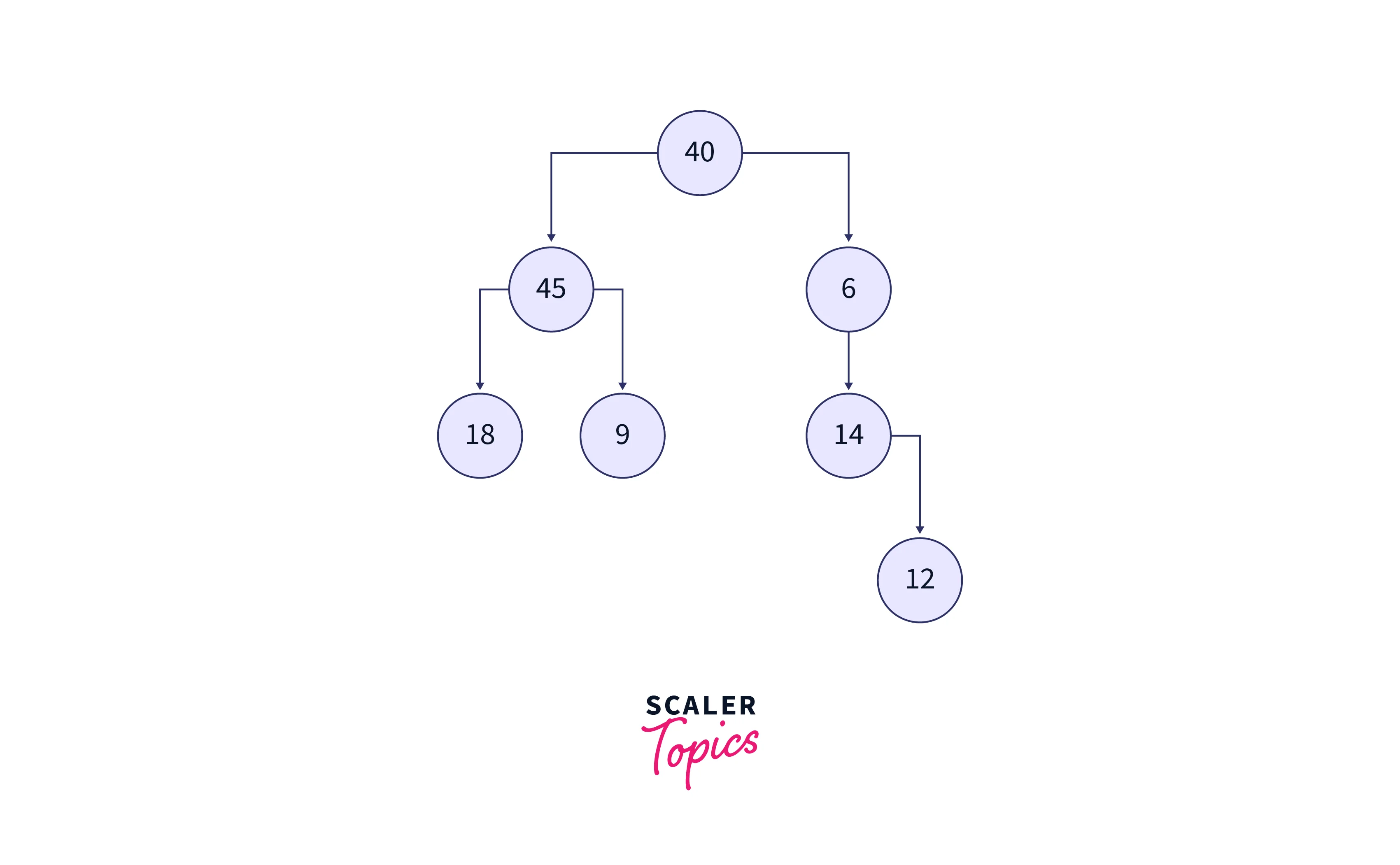
Output:

18 45 9 40 6 14 12

The doubly linked list formed is shown in the below image:

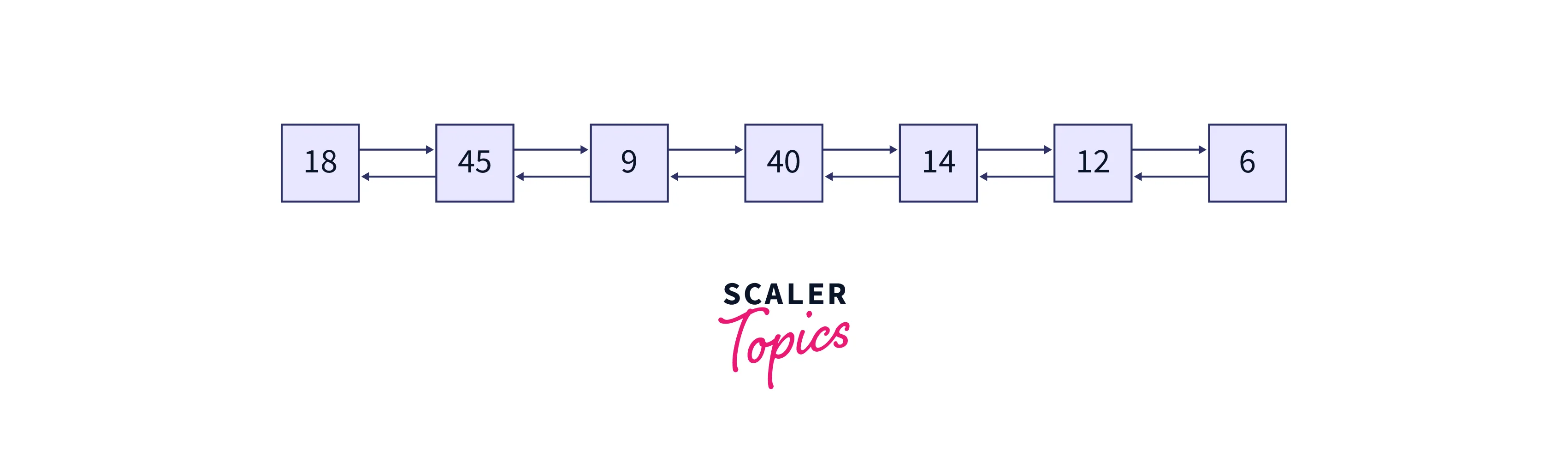
Example Explanation

We can observe that the order of the doubly linked list is the same as the Inorder traversal on the given binary tree. Therefore the nodes of the modified doubly linked list are printed as the output.

Input Format

During competitive programming, the input of the binary tree is given by indicating the value of the data field in each node by providing the root of the binary tree.

Output Format

The output includes printing the node’s values of the newly formed Doubly linked list. Print all the nodes in the doubly linked list.

Constraints

1<=N (Number of nodes in the binary tree) <=10⁵
Value in the data field can be any real number.

Approach 1: By Processing Subtrees

We need to convert the given binary tree to a doubly linked list in place, which means no extra space is needed. So the basic approach can be just manipulating the left and right pointer of the node to the next and previous pointers as in a doubly linked list. We can process the left subtree first and get the head of the doubly linked list, which is the leftmost node in the given binary tree. And by processing the right subtree we get the nodes that are to the right side of the root in the doubly linked list. Using the Inorder predecessor of the root in the left subtree which is considered to be the rightmost node in the left subtree and helps in attaching with the leftmost node of the right subtree and forming a DLL. And also using the Inorder successor of the root in the right subtree which is the leftmost node in the right subtree. The basic idea is to use recursion, to recursively convert each subtree into a doubly linked list.

Algorithm

The below algorithm clearly explains the approach for converting the given binary tree to a doubly linked list:

Here, the idea is the left subtree is processed first and right subtree is processes next as in the Inorder traversal
Check whether the left subtree exists, if it exists then follow the below three steps to convert the left subtree of the root to the doubly linked list:
- Recursively call the left subtree to convert it into a doubly linked list.
- For every call find the Inorder predecessor of the root in the left subtree which is considered to be the next element in the doubly linked list formed.
- After finding the Inorder predecessor, name it as the previous node and now root is the next of the previous node (i.e next of the Inorder predecessor).
Similarly for the right subtree, if the right subtree exists for the root. Follow the below steps if the right subtree of the root node exists:
- Recursively call the right subtree to convert it into a doubly linked list.
- For every recursive call on the right subtree, find the Inorder successor of the root in the right subtree.
- After finding the Inorder successor make this node the next node of the root and root as the previous node of the Inorder successor.
Return the leftmost node of the tree as the head node of the doubly linked list which is formed from the given binary tree.

Implementation

Below is the implementation of the approach which is discussed above for converting the given binary tree to the doubly linked list:

C++ implementation for converting the given binary tree to the doubly linked list by processing subtrees:

// C++ program for converting the binary tree to a doubly linked list
#include <bits/stdc++.h>
using namespace std;
 
// Class of a node in the binary tree 
class Node {
public:
    int val;
    Node* left;
    Node* right;
};

// function which assigns the data to the newly formed node
Node* newNode(int data) {
    Node* new_Node = new Node();
    new_Node->val = data;
    new_Node->left = NULL;
    new_Node->right = NULL;
    return (new_Node);
}
 
// main function which converts the given binary tree to the doubly linked list using recursion
Node* bt_to_dll(Node* root) {
    // Base case when the root is NULL
    if (root == NULL)
        return root;
 
    // Convert the left subtree and link to the root
    if (root->left != NULL) {
        // if the left subtree exists recursively call the function
        Node* left_t = bt_to_dll(root->left);
 
        //  Find in order predecessor which is the right-most node in the subtree
        for (; left_t->right != NULL; left_t = left_t->right);
 
       // Make root as next of Inorder predecessor found
        left_t->right = root;
 
        // and also, make predecessor as previous of root node
        root->left = left_t;
    }
 
    //  Repeat the above steps for the right subtree if it exists
    if (root->right != NULL) {
        // recursively call the right subtree to convert it into a doubly linked list
        Node* right_t = bt_to_dll(root->right);
 
        // Find in order successor, which is the right of the root node
        for (; right_t->left != NULL; right_t = right_t->left);
 
        // Make root as the previous node of the Inorder successor
        right_t->left = root;
 
        // Make the Inorder successor next to the root node
        root->right = right_t;
    }
    // return the root
    return root;
}
 
// Main function which is used to convert the binary tree to DLL using the main recursive function
Node* binaryTree_to_dll(Node* root) {
    // Base case if the root is NULL
    if (root == NULL)
        return root;
 
    // Convert to DLL using bt_to_dll()
    root = bt_to_dll(root);
 
    // the leftmost root is the head of the doubly linked list
    while (root->left != NULL)
        root = root->left;
    // return the head of the doubly linked list
    return (root);
}
 
// Driver code
int main() {
    // Let us create the tree shown in the above diagram
    Node* root = newNode(30);
    root->left = newNode(40);
    root->left->left = newNode(47);
    root->left->right = newNode(19);
    root->left->right->right = newNode(6);
    root->right = newNode(15);
    root->right->left = newNode(21);
    root->right->right = newNode(18);
    root->right->right->left = newNode(14);
 
    // Convert binary tree to DLL
    Node* head = binaryTree_to_dll(root);
    // Print the converted doubly linked list
    while (head != NULL) {
        // print the data present in every node of the doubly linked list
        cout << head->val << " ";
        head = head->right;
    }
    return 0;
}

Python implementation for converting the given binary tree to the doubly linked list by processing subtrees:

# python program to convert the binary tree to a doubly linked list
# class which represents each node in the newly formed doubly linked list
class Node(object):
    # And also binary tree Node class has data, left and right child
    def __init__(self, item):
        self.data = item
        self.left = None
        self.right = None

# main function which converts given a binary tree to the doubly linked list using recursion
def BT_to_DLL(root):
    # base case when the root is None
    if root is None:
        return root
 
    # if left subtree exists recursively call the function
    if root.left:        
        # finding the leftmost node in by calling recursively
        left_t = BT_to_DLL(root.left)
 
        # Find Inorder predecessor which is the right-most node in the subtree
        while left_t.right:
            left_t = left_t.right
 
        # Make root as next of Inorder predecessor found
        left_t.right = root
         
        # and also, make predecessor as previous of root node
        root.left = left_t
 
    # Repeat the above steps for the right subtree if it exists
    if root.right:
        # recursively call the right subtree to convert it into doubly linked list
        right_t = BT_to_DLL(root.right)
 
        # Find in order successor, which is the right
        while right_t.left:
            right_t = right_t.left
 
        # Make root as previous
        # of successor
        right_t.left = root
         
        # Make successor as
        # next of root
        root.right = right_t
 
    return root
# Driver function which is used to convert the binary tree to DLL using the main function 
def BinaryTree_to_DLL(root):
    # base case
    if root is None:
        return root
 
    # Convert to the doubly linked list by using BT_to_DLL and calling it recursively
    root = BT_to_DLL(root)
     
    # to get the leftmost node in the tree because it is the head of the doubly linked list
    while root.left:
        root = root.left
    
    # return the head of the doubly linked list which is formed from the given binary tree
    return root

# Driver Code
if __name__ == '__main__':
    # creatinf the binary tree by giving the values of nodes 
    root = Node(30)
    root.left = Node(40)
    root.left.left = Node(47)
    root.left.right = Node(19)
    root.left.right.right = Node(6)
    root.right = Node(15)
    root.right.left = Node(21)
    root.right.right = Node(18)
    root.right.right.left = Node(14)

    # calling the function which converts the given binary tree to a doubly linked list
    head = BinaryTree_to_DLL(root)
    # printing the nodes in the doubly linked list
    while head:
        #printing the data in the node
        print(head.data, end = " ")
        head = head.right

Java implementation for converting the given binary tree to the doubly linked list by processing subtrees:

// Java program to convert the binary tree to a doubly linked list
// class which represents each node in the newly formed doubly linked list
class Node {
    int val;
    Node left;
    Node right;
    // constructor of the Node class
    Node(int data) {
        val = data;
        left = null;
        right = null;
    }
}
// main class which consists of methods used for converting a binary tree to DLL 
class Solution {
    Node root;
    
    // main function which converts a given binary tree to a doubly linked list using recursion
    Node bt_to_dll(Node root) {
        // Base case when the root is null
        if (root == null)
            return root;
  
        // if left subtree exists recursively call the function
        if (root.left != null) {
             // finding the leftmost node by calling recursively
            Node left_t = bt_to_dll(root.left);
  
            //  Find Inorder predecessor which is the rightmost node in the subtree
            for (; left_t.right != null; left_t = left_t.right);
  
            // Make root as next of Inorder predecessor found
            left_t.right = root;
  
            // and also, make predecessor as previous of root node
            root.left = left_t;
        }
  
        //  Repeat the above steps for right subtree if it exists
        if (root.right != null) {
            // recursively call the right subtree to convert it into a doubly linked list
            Node right_t = bt_to_dll(root.right);
  
            // Find Inorder successor, which is the right
            for (; right_t.left != null; right_t = right_t.left);
  
            // Make root as the previous node of the Inorder successor
            right_t.left = root;
  
            // Make the Inorder successor next to the root node
            root.right = right_t;
        }
         // return the head of the doubly linked list
        return root;
    }
  
    // Main function which is used to convert the binary tree to DLL using the main function 
    Node binaryTree_to_dll(Node node) {
        // Base case when the root is null
        if (node == null)
            return node;
  
        // Convert to DLL using bt_to_dll()
        node = bt_to_dll(node);
  
        // leftmost node is considered as the head of the doubly linked list
        while (node.left != null)
            node = node.left;
         // return the head of the doubly linked list
        return node;
    }
}

class Main{
    // Driver program
    public static void main(String[] args) {
        // creating the binary tree by inserting nodes
        Solution tree = new Solution();
  
        // creating a binary tree by inserting nodes 
        tree.root = new Node(30);
        tree.root.left = new Node(40);
        tree.root.left.left = new Node(47);
        tree.root.left.right = new Node(19);
        tree.root.left.right.right = new Node(6);
        tree.root.right = new Node(15);
        tree.root.right.left = new Node(21);
        tree.root.right.right= new Node(18);
        tree.root.right.right.left = new Node(14);

        // Convert the given bt to dll
        Node head = tree.binaryTree_to_dll(tree.root);
  
        // Print the converted doubly linked list
        while (head != null) {
            // print the data present in every node of the doubly linked list
            System.out.print(head.val + " ");
            head = head.right;
        }
    }
}

Output:

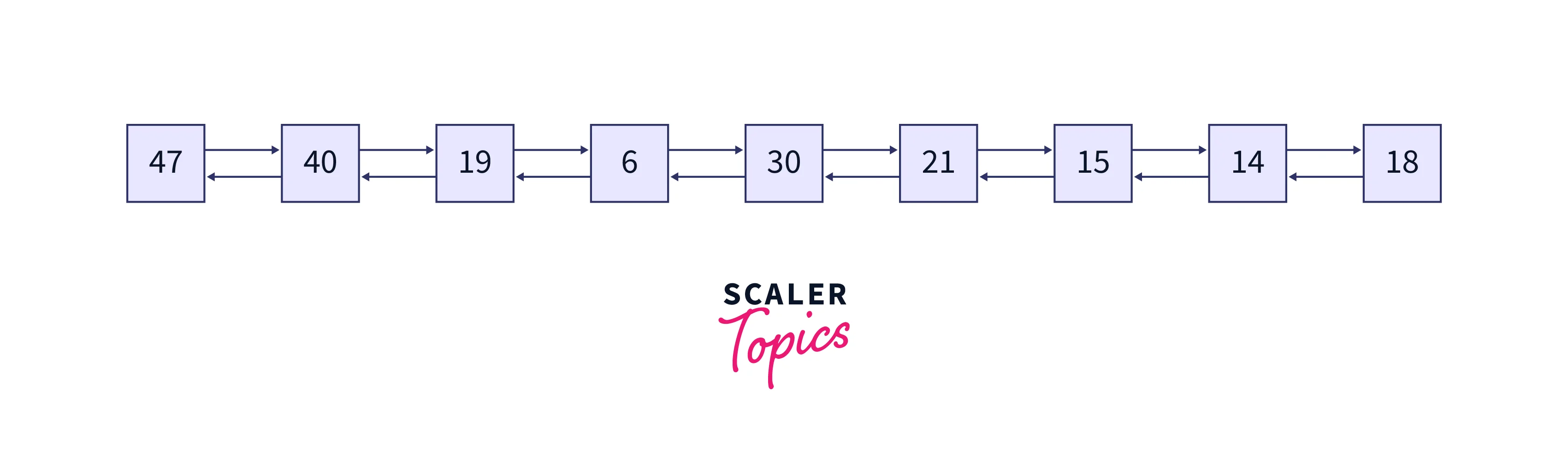
47 40 19 6 30 21 15 14 18

Explanation:

We can observe that the order of the doubly linked list is the same as the Inorder traversal on the given binary tree. The input binary tree is shown in the below.

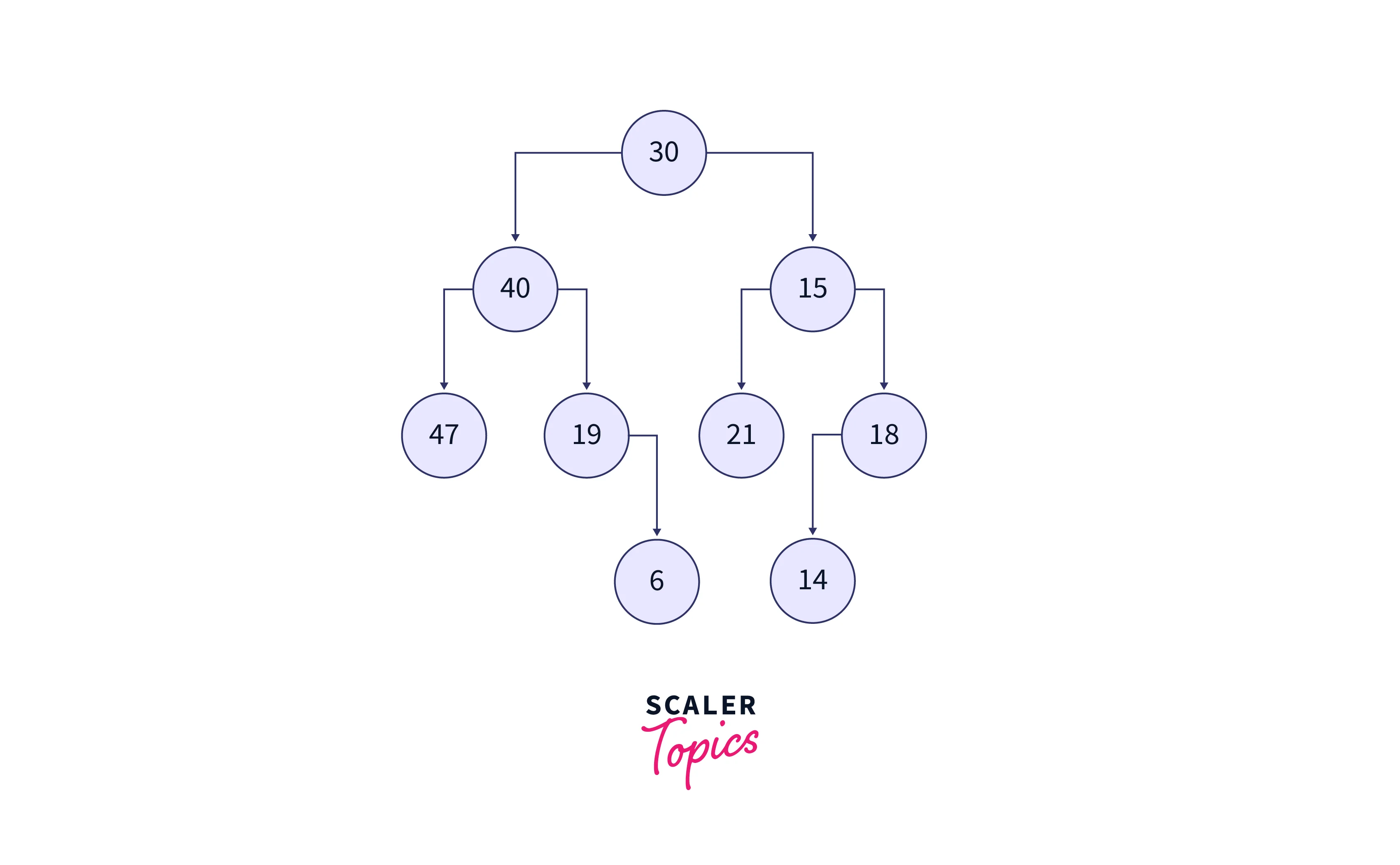
The nodes of the binary tree are converted to the nodes of the doubly linked list. These nodes values are printed as the output. The doubly linked list formed is shown in the below image:

Complexity Analysis

Time Complexity: O(N), where N is the number of nodes present in the given binary tree.

Every node of the binary is traversed once to convert it into the doubly linked list.
Therefore the overall time complexity of this approach is O(N).

Space Complexity: O(N), where N is the number of nodes present in the given binary tree.

Auxiliary stack space used during recursion.

Approach 2: Fixing Left and Right Pointers

A solution for converting the binary tree to a doubly linked list is using the inorder traversal and manipulating the pointers of the root’s right and left pointer as the prev and next pointers as in the doubly linked list. This is can be achieved by simply performing the Inorder traversal on the given binary tree. And changing the left pointer using the previous pointer. Similarly, it changes the right pointer as the next pointer in the doubly linked list.

Algorithm

The below algorithm clearly explains the above-discussed approach for converting the given binary tree to the doubly linked list:

We simply do an Inorder traversal on a tree and keep track of previously visited nodes in the traversal.
For fixing the previous pointers in the DLL, follow the below steps:
- While performing the Inorder traversal on the given binary tree, we keep track of the previously visited node and change the left pointer to the previous node.
For fixing the next pointers in the DLL, follow the below steps:
We use the left pointers of the node which are fixed as previous pointers of the DLL in the above step.
- We start traversing from the rightmost node in the given input binary tree. The rightmost node is however considered to be the last node in a formed doubly linked list. However, left pointers of the node are manipulated to point to the previous node in the doubly linked list.
- Now, we can linearly traverse the modified doubly linked list with the help of these previous pointers. The traversal goes from the rightmost node (last node) to the leftmost node (first node).
- While traversing the modified doubly linked list, we keep track of the previously visited node and modify the right pointer pointing to the previous node of the DLL.

Implementation

Below is the implementation of the approach which is discussed above for converting the given binary tree to the doubly linked list: C++ implementation for converting the given binary tree to the doubly linked list by processing subtrees:

// C++ program for converting the binary tree to a doubly linked list
#include <bits/stdc++.h>
using namespace std;
 
// Class of a node in the binary tree 
class Node {
public:
    int val;
    Node* left;
    Node* right;
};

// function which assigns the data to the newly formed node
Node* newNode(int data) {
    Node* new_Node = new Node();
    new_Node->val = data;
    new_Node->left = NULL;
    new_Node->right = NULL;
    return (new_Node);
}
// Changes left pointers to as previous pointers in the newly converted dll 
void ChangePrevPtr(Node *root) {
    static Node *pre = NULL;
    if (root != NULL) {
        // converting it recursively 
        //keeping track of the previously visited node while doing an Inorder traversal on the binary tree
        ChangePrevPtr(root->left);
        root->left = pre;
        pre = root;
        // making them as the previous nodes in the dll 
        ChangePrevPtr(root->right);
    }
}
 
// Changes right pointers to as next pointers in converted DLL
Node *ChangeNextPtr(Node *node) {
    // assume the prev is initially None
    Node *previous = NULL;
 
    // For finding the rightmost node in Binary which is also the last node in the dll
    while (node && node->right != NULL)
        node = node->right;
 
    // Start from the rightmost node, traverse back to the previous nodes using the left pointers which are manipulated in the above function
    // While traversing change the right pointer of nodes as the next nodes in the dll
    while (node && node->left != NULL) {
        previous = node;
        node = node->left;
        node->right = previous;
    }
 
    // Return the head of the DLL, which is the leftmost node in the given binary tree
    return (node);
}
 
// The main function that converts BST to DLL and returns the head of the converted DLL
Node *BinaryTree_to_DLL(Node *root) {
    // Adjusts the previous pointers of the converted dll
    ChangePrevPtr(root);
    // Adjusts the next pointers of the converted DLL and returns the head of the dll 
    return ChangeNextPtr(root);
}

// Driver code
int main() {
    // Let us create the tree shown in the above diagram
    Node* root = newNode(29);
    root->left = newNode(-10);
    root->left->left = newNode(56);
    root->left->right = newNode(49);
    root->left->right->left = newNode(8);
    root->right = newNode(4);
    root->right->right = newNode(1);
    root->right->right->left = newNode(-14);
    root->right->right->left->right = newNode(17);
 
    // Convert binary tree to DLL
    Node* head = BinaryTree_to_DLL(root);
    // Print the converted doubly linked list
    while (head != NULL) {
        // print the data present in every node of the doubly linked list
        cout << head->val << " ";
        head = head->right;
    }
    return 0;
}

Python implementation for converting the given binary tree to the doubly linked list by processing subtrees:

# Python program to convert the binary tree to dll
# node of a binary tree
class Node:
    # Constructor to create a new tree node
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None
        
# Changes left pointers to as previous pointers in the newly converted dll
def ChangePrevPtr(root):
    if root is not None:
        # converting it recursively 
        # keeping track of the previously visited node while doing an Inorder traversal on the binary tree
        ChangePrevPtr(root.left)
        root.left = ChangePrevPtr.pre
        ChangePrevPtr.pre = root
        # making them as the previous nodes in the dll 
        ChangePrevPtr(root.right)
 
# Changes right pointers to as next pointers in converted DLL
def ChangeNextPtr(node):
    
    # assume the prev is initially None
    prev = None
    # For finding the rightmost node in Binary which is also the last node in the dll
    while(node and node.right != None):
        node = node.right
 
    # Start from the rightmost node, and traverse back to the previous nodes using the left pointers which are manipulated in the above function
    # While traversing change the right pointer of nodes as the next nodes in the DLL
    while(node and node.left != None):
        prev = node
        node = node.left
        node.right = prev
 
    # Return the head of the DLL, which is the leftmost node in the given binary tree
    return node
 
# The main function that converts BST to DLL and returns
# the head of DLL
def BinaryTree_to_DLL(root):
     
    # Adjusts the previous pointers of the converted dll
    ChangePrevPtr(root)
 
    # Adjusts the next pointers of the converted DLL and returns the head of the dll 
    return ChangeNextPtr(root)

# driver code
if __name__ == '__main__':
    # creatinf the binary tree by giving the values of nodes 
    root = Node(29)
    root.left = Node(-10)
    root.left.left = Node(56)
    root.left.right = Node(49)
    root.left.right.left = Node(8)
    root.right = Node(4)
    root.right.right = Node(1)
    root.right.right.left = Node(-14)
    root.right.right.left.right = Node(17)
    # Static variable pre for function fixPrevPtr
    ChangePrevPtr.pre = None
    # calling the function which converts the given binary tree to a doubly linked list
    head = BinaryTree_to_DLL(root)
    # printing the nodes in the doubly linked list
    while head:
        #printing the data in the node
        print(head.val, end = " ")
        head = head.right

Java implementation for converting the given binary tree to the doubly linked list by processing subtrees:

// Java program to convert the binary tree to a doubly linked list
public class Main{
    // class which represents each node in the newly formed doubly linked list
    static class Node {
        int val;
        Node left;
        Node right;
        // constructor for creating the new node in the tree
        public Node(int val){
            this.val = val;
        }
    }
    // assume the prev is initially None
    static Node prev;
 
    //  Changes left pointers to as previous pointers in the newly converted dll
    static void ChangePrevptr(Node root) {
        // base case
        if (root == null)
            return;
        // converting it recursively 
        //keeping track of the previously visited node while doing an Inorder traversal on the binary tree
        ChangePrevptr(root.left);
        root.left = prev;
        prev = root;
        ChangePrevptr(root.right);
    }
 
    // Changes right pointers to as next pointers in converted DLL
    static Node ChangeNextptr(Node node) {       
        // For finding the rightmost node in Binary which is also the last node in the DLL
        while (node.right != null)
            node = node.right;
 
        // Start from the rightmost node, traverse back to the previous nodes using the left pointers which are manipulated in the above function
        // While traversing change right pointer of nodes as the next nodes in the DLL
        while (node != null && node.left != null) {
            Node left_t = node.left;
            left_t.right = node;
            node = node.left;
        }
 
        // Return the head of the DLL, which is the leftmost node in the given binary tree
        return node;
    }
     // The main function that converts BST to DLL and returns the head of DLL
    static Node binaryTree_to_dll(Node root) {
        prev = null;
 
        // Adjusts the previous pointers of the converted dll
        ChangePrevptr(root);
        // Adjusts the next pointers of the converted DLL and returns the head of the dll 
        return ChangeNextptr(root);
    }
 
   // Driver program
    public static void main(String[] args) {
        // creating a binary tree by inserting nodes 
        Node root = new Node(29);
        root.left = new Node(-10);
        root.left.left = new Node(56);
        root.left.right = new Node(49);
        root.left.right.left = new Node(8);
        root.right = new Node(4);
        root.right.right = new Node(1);
        root.right.right.left = new Node(-14);
        root.right.right.left.right = new Node(17);
      
        // Convert the given bt to dll
        Node head = binaryTree_to_dll(root);
  
        // Print the converted doubly linked list
        while (head != null) {
            // print the data present in every node of the doubly linked list
            System.out.print(head.val + " ");
            head = head.right;
        }
    }
}

Output:

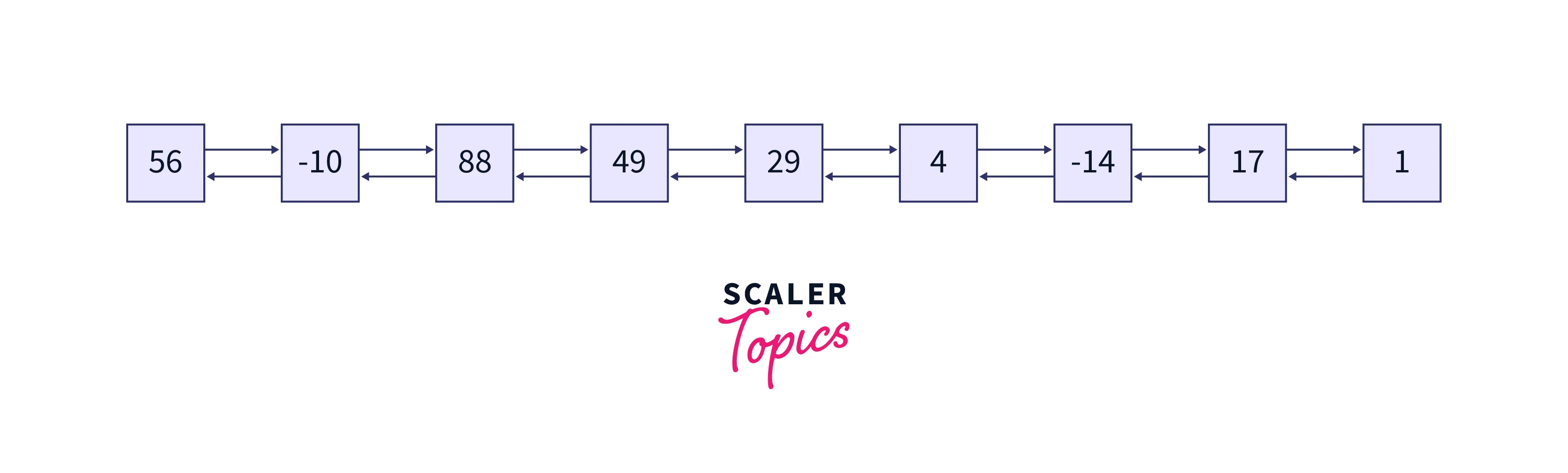
56 -10 8 49 29 4 -14 17 1

Explanation:

We can observe that the order of the doubly linked list is the same as the Inorder traversal on the given binary tree. The input binary tree is shown in the below image.

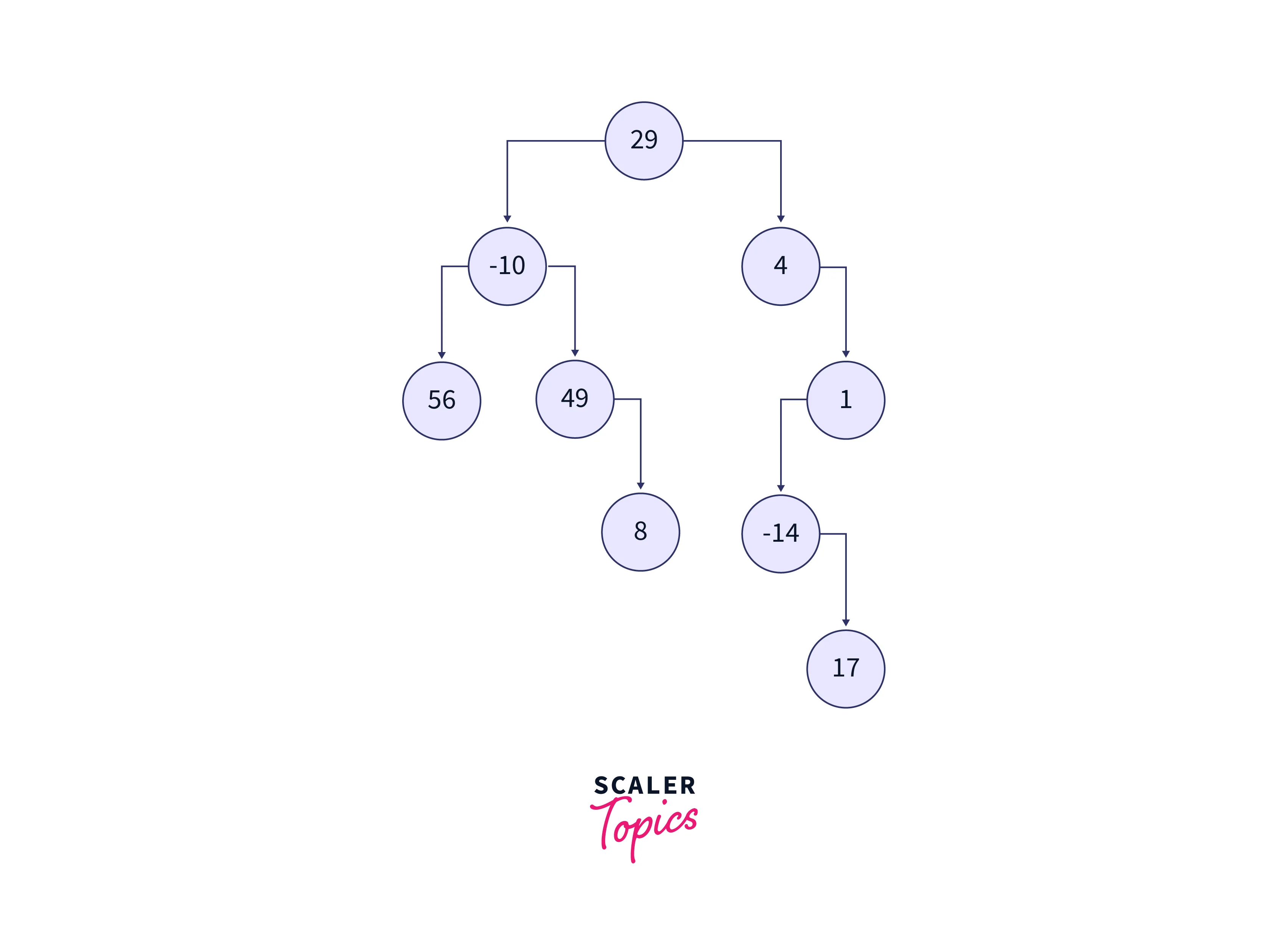
The nodes of the binary tree are converted to the nodes of the doubly linked list. These nodes’ values are printed as the output. The doubly linked list formed is shown in the below image:

Complexity Analysis:

Time Complexity: O(N), where N is the number of nodes present in the given binary tree.

Every node of the binary is traversed twice to convert it into the doubly linked list. Because two traversals are performed on the tree.
One traversal is performed to change the left pointers as the previous pointers and the other traversal for changing the right pointers as the next pointers in the doubly linked list.
Therefore the overall time complexity of this approach is O(N).

Space Complexity: O(N), where N is the number of nodes present in the given binary tree.

An auxiliary stack space of O(N) is used during recursion to keep track of the visited nodes during the Inorder traversal which is performed on the given tree.

Approach 3: Inorder Traversal (By Keeping Track Of DLL Head and Tail Pointers)

All the approaches discussed earlier deals with Inorder traversal and manipulating the left and right pointers of a node as the prev and next pointers to convert it into a doubly linked list. Similarly, this approach uses recursion to recursively convert the left subtree and right subtree separately and convert them into a doubly linked list. While traversing each node keep track of the head node and tail node of the DLL.

Algorithm

The below algorithm converts the given binary tree into a doubly linked list using recursion:

Firstly, traverse the whole binary tree in an Inorder manner (left node of the root is processed first, the present node is inserted into the DLL with the help of the tail pointer, then the right node is processed).
For every node which is visited, keep track of the head and tail pointers that are initialized for a doubly linked list.
Insert every visited node to the end of the doubly linked list with the help of the tail pointer. By adding it to the tail pointer.
Head pointer always has the first node of the doubly linked list.
Return the head pointer at the end of all recursive calls i.e, when all the nodes in the tree are visited.

Implementation

Below is the implementation of the approach which is discussed above for converting the given binary tree to the doubly linked list.

C++ implementation for converting the given binary tree to the doubly linked list by processing subtrees:

// C++ program for converting the binary tree to a doubly linked list
#include <bits/stdc++.h>
using namespace std;
 
// Class of a node in the binary tree 
class Node {
public:
    int val;
    Node* left;
    Node* right;
};

// function which assigns the data to the newly formed node
Node* newNode(int data) {
    Node* new_Node = new Node();
    new_Node->val = data;
    new_Node->left = NULL;
    new_Node->right = NULL;
    return (new_Node);
}
// recursive function which helps in converting the Binary tree to dll 
// head is the head of the formed dll
// tail is the ending node of the formed dll
// initially they are null
void bt_to_dll(Node* root, Node** head, Node** tail) {
    // base case if the root is NULL
    if (root == NULL)
        return;
    // recursively call for the left subtree of the root
    bt_to_dll(root->left, head, tail);
    
    // if the head is null that means the root is the first node in the dll
    if (*head == NULL) {
        *head = root;
    }
    
    // make tail as the root to the left node
    root->left = *tail;
    
    // finding the last rightmost node which is the tail of the dll
    if (*tail != NULL) 
        // finding the tail of the dll
        (*tail)->right = root;
    
        // assign root as the tail node
    *tail = root;
    
    // recursively call for the right subtree of the root
    bt_to_dll(root->right, head, tail);
}
 
// The main function which helps in calling the recursive function which is mentioned above
Node* BinaryTree_to_DLL(Node* root) {
    // Base case
    if (root == NULL)
        return root;
    //initializing the head and tail pointer as NULL
    Node* head = NULL;
    //initializing the tail pointer of the dll
    Node* tail = NULL;
    
    // passing root, head, and tail for the recursive function to convert the given binary tree to dll
    bt_to_dll(root, &head, &tail);
    
    // return the head of the converted dll
    return head;
}
// Driver code
int main() {
    // Let us create the tree shown in the above diagram
    Node* root = newNode(10);
    root->left = newNode(8);
    root->left->left = newNode(14);
    root->left->right = newNode(94);
    root->right = newNode(16);
    root->left->left->left = newNode(27);
    root->left->left->left->right = newNode(29);
    
 
    // Convert binary tree to DLL
     Node* head = BinaryTree_to_DLL(root);
    // Print the converted doubly linked list
    while (head != NULL) {
        // print the data present in every node of the doubly linked list
        cout << head->val << " ";
        head = head->right;
    }
    return 0;
}

Python implementation for converting the given binary tree to the doubly linked list by processing subtrees:

# Python program to convert the binary tree to dll
# node of a binary tree
class Node:
    # Constructor to create a new tree node
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None

# intialising the global variables which are the head and tail of the DLL
head,tail=None,None
# Recusive function which helps in converting the binary tree to the doubly linked list
def bt_to_dll(root):
    # base case 
    if (root == None):
        return
    # getting the left and right pointers of the DLL
    left = root.left
    right = root.right
    
    # global variables which are the head and tail of the DLL
    global head
    global tail
    
    # recursive calls for the left subtree of the root
    bt_to_dll(root.left)
    
    # base case
    if (head == None):
        head = root
     
    root.left = tail
    
    #rightmost node is the tail of the converted DLL
    if (tail != None):
        tail.right = root
         
    tail = root
    
    # recursively call for the right side of the root(right subtree)
    bt_to_dll(root.right)
 
# main function which calls the recursive function and helps in converting the binary tree to dll
def BinaryTree_to_DLL(root):
    # Base case
    global head
    if (root == None):
        head = root
    # calling the recursive function 
    bt_to_dll(root)
    
# driver code
if __name__ == '__main__':
    # creatinf the binary tree by giving the values of nodes 
    root = Node(10)
    root.left = Node(8)
    root.left.left = Node(14)
    root.left.right = Node(94)
    root.left.left.left = Node(27)
    root.left.left.left.right = Node(29)
    root.right = Node(16)
    
    
    # calling the function which converts the given binary tree to a doubly linked list
    BinaryTree_to_DLL(root)
    # printing the nodes in the doubly linked list
    while head:
        #printing the data in the node
        print(head.val, end = " ")
        head = head.right

Java implementation for converting the given binary tree to the doubly linked list by processing subtrees:

// Java program to convert the binary tree to a doubly linked list
public class Main{
    // class which represents each node in the newly formed doubly linked list
    static class Node {
        int val;
        Node left;
        Node right;
        // constructor for creating the new node in the tree
        public Node(int val){
            this.val = val;
        }
    }
    //initializing the global variables which are the head and tail of the DLL
    static Node head, tail;
    //  Recursive function which helps in converting the binary tree to the doubly linked list
    static void bt_to_dll(Node root) {
        // base case if the root is null 
        if (root == null)
            return;
        
        // getting the left and right pointers of the dll
        Node left = root.left;
        Node right = root.right;
        
        // recursive calls for the left subtree of the root
        bt_to_dll(root.left);
        
        // base case if the head is null, it means it is the starting point of the dll
        if (head == null) 
            head = root;
        
        
        root.left = tail;
        
        // rightmost node is the tail of the converted DLL
if (tail != null) 
            (tail).right = root;
        
        
        tail = root;
        //  recursively call for the right side of the root(right subtree)
        bt_to_dll(root.right);
    }
 
    // main function which calls the recursive function and helps in converting the binary tree to dll
    static void binaryTree_to_dll(Node root) {
 
        // Base case
        if (root == null)
            head = root;
        // calling the recrusive function 
        bt_to_dll(root);
    }
    
   // Driver program
    public static void main(String[] args) {
        // creating a binary tree by inserting nodes 
        Node root = new Node(10);
        root.left = new Node(8);
        root.left.left = new Node(14);
        root.left.right = new Node(94);
        root.left.left.left = new Node(27);
        root.left.left.left.right = new Node(29);
        root.right = new Node(16);
        
        // Convert the given bt to dll
        binaryTree_to_dll(root);
  
        // Print the converted doubly linked list
        while (head != null) {
            // print the data present in every node of the doubly linked list
            System.out.print(head.val + " ");
            head = head.right;
        }
    }
}

Output:

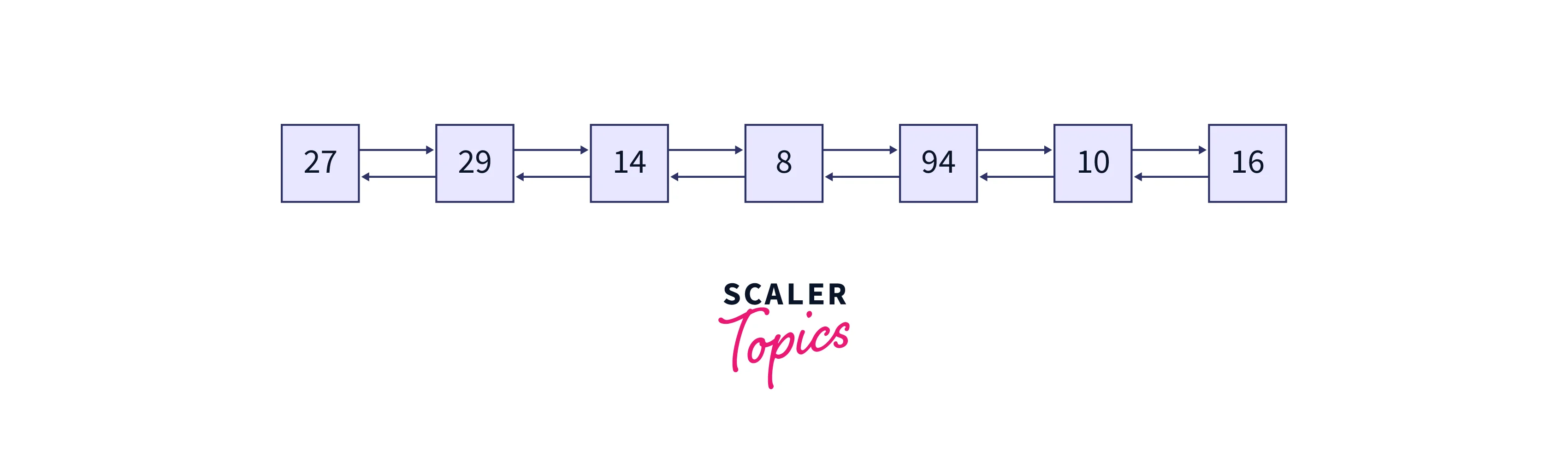
27 29 14 8 94 10 16

Explanation: We can observe that the order of the doubly linked list is the same as the Inorder traversal on the given binary tree. The input binary tree is shown in the below image.

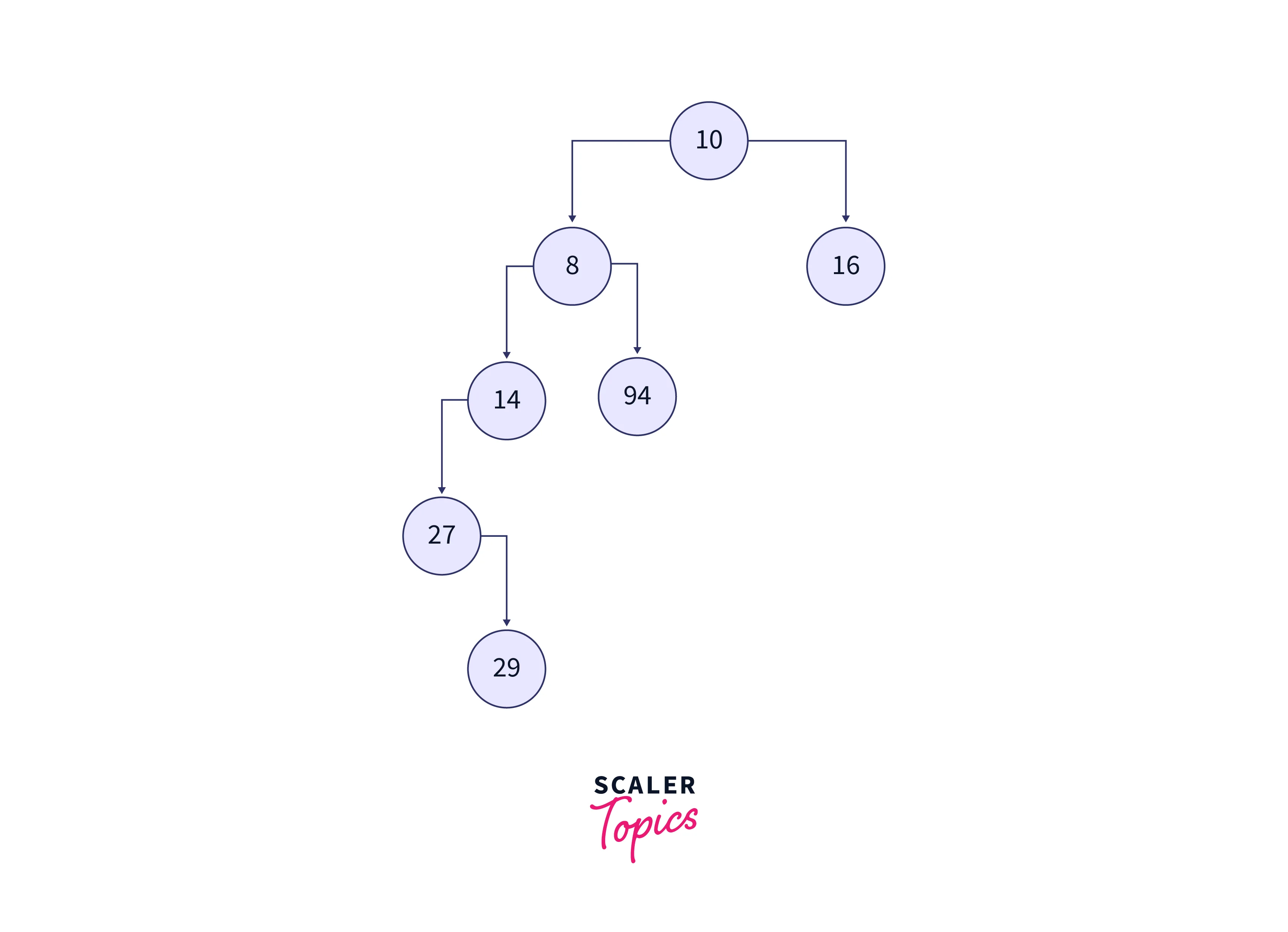
The nodes of the binary tree are converted to the nodes of the doubly linked list. These nodes’ values are printed as the output. The doubly linked list formed is shown in the below image:

Complexity Analysis

Time Complexity: O(N), where N is the number of nodes present in the given binary tree.

Every node of the binary is traversed once during the Inorder traversal and converted into head and tail pointers as in the doubly linked list.
Therefore the overall time complexity of this approach is O(N).

Space Complexity: O(N), where N is the number of nodes present in the given binary tree.

Auxiliary stack space used during recursion for Inorder traversal performed on the given input binary tree.

Conclusion

This article explained different approaches used to convert a given binary tree into a doubly linked list.
All the approaches dealt with manipulating the left and right pointers of the tree into prev and next pointers as in the doubly linked list.
Every approach uses Inorder traversal while converting into a doubly linked list.
Time complexity of all the approaches is O(N), and space complexity is O(N). The difference between all the approaches is how the pointers are changed to make it a doubly linked list.
Please refer to Part 2 of this editorial for recursive and iterative approach.

Author

Sindhuja Gudala

View all posts

Convert Binary Tree to Doubly Linked List – Part I

Problem Statement

Example

Example Explanation

Input Format

Output Format

Constraints

Approach 1: By Processing Subtrees

Algorithm

Implementation

Complexity Analysis

Approach 2: Fixing Left and Right Pointers

Algorithm

Implementation

Complexity Analysis:

Approach 3: Inorder Traversal (By Keeping Track Of DLL Head and Tail Pointers)

Algorithm

Implementation

Complexity Analysis

Conclusion

Author

Latest articles

Largest Number Formed from an Array

Fundamentals of Enhanced Interior Gateway Routing Protocol

What is Network Hub?

Largest Number Formed from an Array

Fundamentals of Enhanced Interior Gateway Routing Protocol

What is Network Hub?

Convert Binary Tree to Doubly Linked List – Part I

Problem Statement

Example

Example Explanation

Input Format

Output Format

Constraints

Approach 1: By Processing Subtrees

Algorithm

Implementation

Complexity Analysis

Approach 2: Fixing Left and Right Pointers

Algorithm

Implementation

Complexity Analysis:

Approach 3: Inorder Traversal (By Keeping Track Of DLL Head and Tail Pointers)

Algorithm

Implementation

Complexity Analysis

Conclusion

Author

Latest articles

Largest Number Formed from an Array

Fundamentals of Enhanced Interior Gateway Routing Protocol

What is Network Hub?

Featured articles

Largest Number Formed from an Array

Fundamentals of Enhanced Interior Gateway Routing Protocol

What is Network Hub?