Bubble Sort Algorithm

Bubble Sort, a basic sorting algorithm, operates by repeatedly swapping adjacent elements if they are incorrectly ordered. Consider a list with elements 5, 4, 3, and 2; sorting algorithms like Bubble Sort can organize them in either ascending or descending order, rearranging elements to form meaningful sequences, as illustrated in this example.

Ascending Sorting  Descending Sorting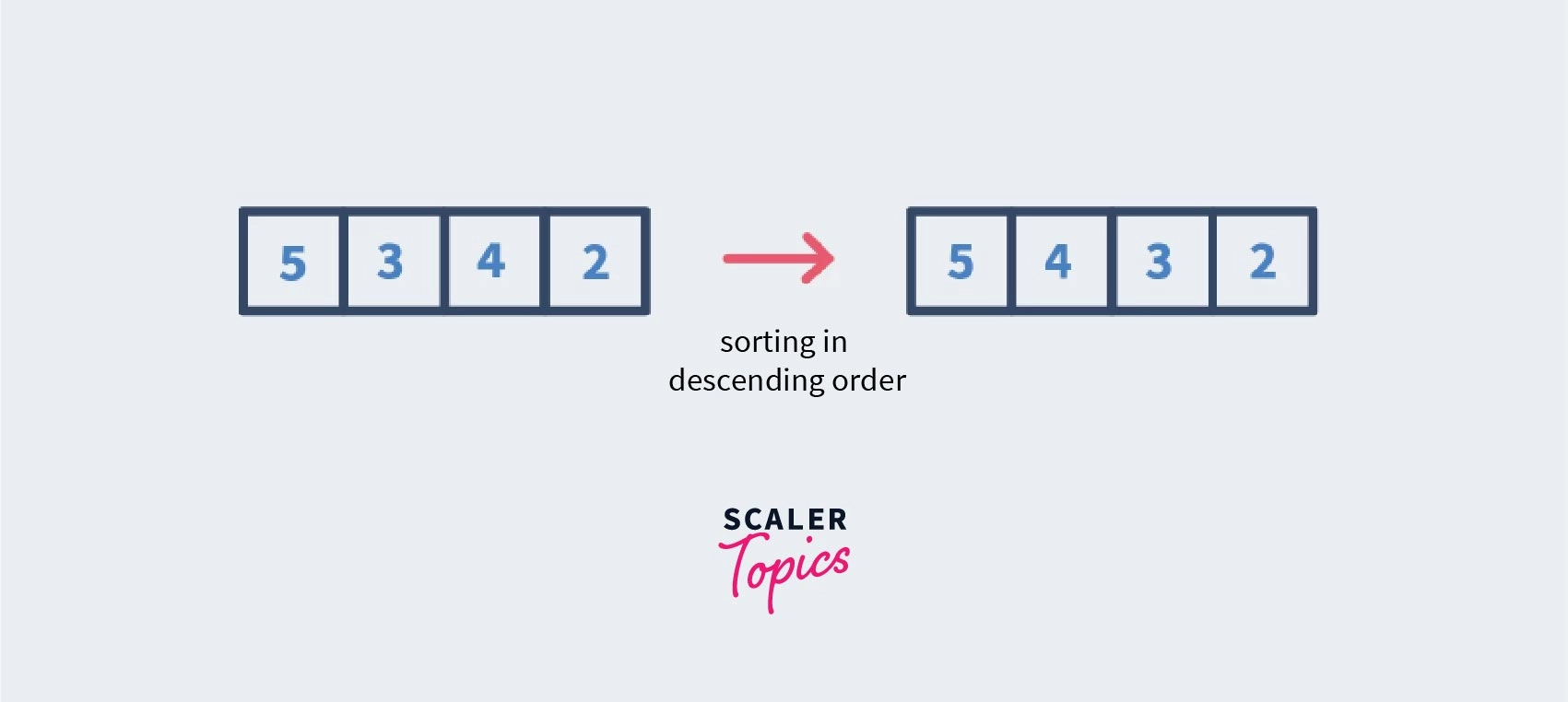 

There are multiple algorithms that can be used for sorting. And, in this article, we will discuss Bubble sort in the following order –

So let us now gear ourselves up to dive deeper and understand what bubble sort is.

Working of Bubble Sort

Consider that we want to sort a list in ascending order, here are the steps that the algorithm would follow:

1. Start with the first element.
2. Compare the current element with the next element.
3. If the current element is greater than the next element, then swap both the elements. If not, move to the next element.
4. Repeat steps 1 – 3 until we get the sorted list. To better understand bubble sort, recall the list that contains the elements 5, 3, 4, 2 initially.

The steps to sort this list would involve –

From the above-given diagram, we can infer the following conclusions about the bubble sort algorithm –

1. In bubble sort, to sort a list of size n, we need to perform n – 1 iterations. Notice we had 4 elements with us, and we got the sorted list in 3 passes. This is because each time we iterate over the list, an element gets sorted. This element is left in the next iteration of the loop. While we reach the (n – 1)th iteration, we are only left with one number. And, since a minimum of two numbers is required for comparison, that number can not be compared further.
2. In the first pass, the highest element (5 in this case) was bubbled out on the right side of the list. Similarly, after each iteration, the largest among the unsorted elements was placed at its position. This is the reason why this sorting algorithm is known as bubble sort.
3. In the second pass, we did not compare elements 4 and 5. This is because we know that 5 is already at its correct position, and comparing them would not make any difference. Same for 3 & 4 and 4 & 5 in the third pass. In each pass, comparison occurs up to the last unsorted element. This way we can reduce the number of comparisons.
4. Element 2 took a significant number of passes to arrange itself at its position in the sorted list. Thus, if any element of the list takes more passes, it is known as the turtle. Whereas element 5 took only one pass to reach its position, which is rare for bubble sort. Such elements are known as rabbits due to a low number of passes.

Imagine this. You are traveling on a straight road, and five cars are running at different speeds. For the sake of simplicity, let us assume that each of them is maintaining its respective speed.

What will happen if any car is moving faster than the one in front? Yes, the car at the back would overtake the one at the front. This way, the cars with the higher speed will occupy the position of the cars with the lower speed.

Now, following this, every car starts overtaking any car slower than itself. Eventually, the car with the highest speed will occupy the first position on the road, followed by the second-fastest car, and so on.

Notice how we used bubble sort to sort cars according to their speed. Here, with every overtake we were comparing the speeds of the cars, and if the car at the back was faster than the car at the front, they exchanged their positions, just like it is done in bubble sort.

Now that we have understood what bubble sort is, let us see how to implement a bubble sort algorithm via codes.

Bubble Sort Algorithm

We know that to sort a list of n elements using bubble sort, we need to perform n – 1 iterations. And for each iteration, we need to:

1. Run a loop over the entire list or array.
2. Compare the element at the index i with the element at i + 1.
3. If the element at i is greater than the element at i + 1, swap both the elements
4. Else, move to the next element.

begin bubbleSort(list)
 
for i = 0 to sizeof(list) - 1    
    for j = 0 to sizeof(list) - i - 1
        if list[j] > list[j+1]
             swap(list[i], list[i+1])
        end if
    end for
end for
 
end bubbleSort

Implementation of Bubble Sort

1. Bubble Sort Code in Java

// Bubble sort in Java
class Main {
 
  // bubble sort
  static void bubbleSort(int arr[]) {
    int size = arr.length;
    
    // loop over array elements
    for (int i = 0; i < size - 1; i++)
    
      // loop to compare array elements
      for (int j = 0; j < size - i - 1; j++)
 
        // compare two adjacent elements
        if (arr[j] > arr[j + 1]) {
 
          //swap if elements are out-of-order
          int temp = arr[j];
          array[j] = array[j + 1];
          array[j + 1] = temp;
        }
  }
}

2. Bubble Sort Code in Python

# Bubble sort in Python
 
def bubbleSort(arr):
    
  # loop over array elements
  for i in range(len(arr)-1):
 
    # loop to compare array elements
    for j in range(0, len(arr) - i - 1):
 
      # compare two adjacent elements
      if arr[j] > arr[j + 1]:
 
        # swap if elements are out-of-order
        temp = arr[j]
        arr[j] = arr[j+1]
        arr[j+1] = temp

3. Bubble Sort Code in C

// Bubble sort in C
// bubble sort function
void bubbleSort(int arr[], int size) {
 
  // loop over array elements
  for (int i = 0; i < size - 1; ++i) {
      
    // loop to compare array elements
    for (int j = 0; j < size - i - 1; ++j) {
      
      // compare two adjacent elements
      if (arr[j] > arr[j + 1]) {
        
        // swap if elements are out-of-order
        int temp = arr[j];
        arr[j] = arr[j + 1];
        arr[j + 1] = temp;
      }
    }
  }
}

4. Bubble Sort Code in C++

// Optimized Bubble sort in C++
// perform the bubble sort
void bubbleSort(int arr[], int size) {
 
  // // loop over array elements
  for (int i = 0; i < size - 1; ++i) {
    
    // loop to compare array elements
    for (int j = 0; j < size - i - 1; ++j) {
      
      // compare adjacent elements
      if (arr[j] > arr[j + 1]) {
        
        // swap if out-of-order
     // using std::swap() method for swapping
        swap(arr[j], arr[j+1]);
      }
    }
  }
}

Optimized Bubble Sort Algorithm

Imagine the case where the list is already sorted. For example, our input list contains 2, 3, 4, 5 instead of 5, 3, 4, 2.

In the above algorithm, the loop would still run to compare all the elements. It might cause complex issues like longer execution times.

To tackle this, we can do the following:

• Create a flag variable, called swapped.
• The value of the swap is set to true if, during any iteration, swapping was done.
• Else, the value of the swap is set to false.
• After an iteration, if the value of swapped is found to be false, it means the array is sorted, and no more comparisons are required.
• We then stop the execution.

It will help in reducing the number of comparisons, and hence the execution time of the algorithm.

Pseudocode

begin bubbleSort (array)
 
   size = length of array;
   
   for i = 0 to loop-1:
      swapped = false
    
      for j = 0 to loop - i - 1:
      
         /* compare the adjacent elements */   
         if list[j] > list[j+1] then
            /* swap them */
            swap( list[j], list[j+1] )     
            swapped = true
         end if
         
      end for
      
      /*if no number was swapped that means 
      array is sorted now, break the loop.*/
      
      if(not swapped) then
         break
      end if
      
   end for
   
end bubbleSort

Notice the part where if the value of swapped is false, we stop the execution of the loop. It is done because we have already obtained a sorted list.

Now let us implement the above pseudocode in Java, Python, C, and C++.

Optimized Implementation of Bubble Sort

1. Optimized Bubble Sort Code in Java

// Optimized Bubble sort in Java
class Main {
 
  // perform the bubble sort
  static void bubbleSort(int arr[]) {
    int size = arr.length;
    
    // loop over array elements
    for (int i = 0; i < (size-1); i++) {
    
      // swapped variable initially set to false
      boolean swapped = false;
      
      // compare adjacent elements
      for (int j = 0; j < (size-i-1); j++) {
 
        // comparing adjacent elements
        if (arr[j] > arr[j + 1]) {
 
          // swapp if out-of-order
          int temp = arr[j];
          arr[j] = arr[j + 1];
          arr[j + 1] = temp;
          
    // set swap to true after swapping is performed
          swapped = true;
        }
      }
 
      // array is already sorted, not need to compare further
      if (!swapped)
        break;
    }
  }
}

2. Optimized Bubble Sort Code in Python

# Optimized Bubble sort in Python
 
def bubbleSort(arr):
    
  # loop over array elements
  for i in range(len(arr)-1):
        
    # swapped variable initially set to false
    swapped = False
    
    for j in range(0, len(arr) - i - 1):
 
      # compare adjacent elements
      if arr[j] > arr[j + 1]:
 
        # swap if out-of-order
        temp = arr[j]
        arr[j] = arr[j+1]
        arr[j+1] = temp
  
     # set swap to true after swapping is performed
        swapped = True
          
    # array is already sorted, not need to compare further
    if not swapped:
      break

3. Optimized Bubble Sort Code in C

// Optimized Bubble sort in C
 
// perform the bubble sort
void bubbleSort(int arr[], int size) {
 
  // // loop over array elements
  for (int i = 0; i < size - 1; ++i) {
    
    // swapped variable initially set to 0  
    int swapped = 0;
    
    // loop to compare array elements
    for (int j = 0; j < size - i - 1; ++j) {
      
      // compare adjacent elements
      if (arr[j] > arr[j + 1]) {
        
        // swap if out-of-order
        int temp = arr[j];
        arr[j] = arr[j + 1];
        arr[j + 1] = temp;
        
        swapped = 1;
      }
    }
    
    // array is already sorted, not need to compare further
    if (swapped == 0) {
      break;
    }
    
  }
}

4. Optimized Bubble Sort Code in C++

// Optimized Bubble sort in C++
// perform the bubble sort
void bubbleSort(int arr[], int size) {
 
  // // loop over array elements
  for (int i = 0; i < size - 1; ++i) {
    
    // swapped variable initially set to 0  
    int swapped = 0;
    
    // loop to compare array elements
    for (int j = 0; j < size - i - 1; ++j) {
      
      // compare adjacent elements
      if (arr[j] > arr[j + 1]) {
        
        // swap if out-of-order
    //using std::swap() method for swapping
        swap (arr[j], arr[j+1]);
        
        swapped = 1;
      }
    }
    
    // array is already sorted, not need to compare further
    if (swapped == 0) {
      break;
    }
    
  }
}

Bubble Sort Complexity

1. Time Complexity

To better understand the time complexity, let us break the bubbleSort() function into the following parts:

Loop to iterate over the entire list Loop to iterate over the list to compare the next element. Let the number of elements in the list be n. Now, we know that for part 1, the loop would run for n times.

In part 1, each iteration of the loop would take constant time. Therefore, for part 1, we can say that time complexity would be O(n).

Part 2 is nested inside the loop that is run in part 1. Under this part, n comparisons are made that take constant time for execution. In other words, for each time part 1 is executed, part 2 will be executed n times. And if part 1 is executed for n number of times, part 2 would be executed for n * n number of times.

From this, we can say that the complexity of the selection sort algorithm is O(n²).

Now let us discuss the time complexity in best, average, and the worst case.

• Worst Case: O(n²). The worst case occurs when we want to sort a list in ascending order, but it is arranged in descending order.
• Average Case: O(n²). The average case is when the list is arranged in a jumbled order.
• Best Case: O(n). The best case occurs when the list is already arranged in the desired order.

Therefore, the time complexity of a bubble sort algorithm is O (n²).

Recall the part where we had concluded that to sort a list of n elements, we need to perform n – 1 passes. And for each pass, we need to run a loop to iterate over the list. Now since the complexity of a for loop is O(n), and we are using two nested for loops, the time complexity of bubble sort can be explained as –

(n – 1) * (( n – 2) + (n – 3) + (n – 4) +….1 ), which would be equal to n * (n – 1)/2. And, in Big-Oh notation, this would be O(n²).

2. Space Complexity

• Simple Bubble Sort – The space complexity of the simple bubble sort algorithm is O(1). This is because we have used a fixed number of variables, and we do not need any extra memory space apart from the loop variables and auxiliary variable that includes temp. It means that we can sort an array containing a thousand elements even without using any extra variable
• Optimized Bubble Sort – The space complexity of the simple bubble sort algorithm is O(2). This is because we are using 2 extra variables – temp for swapping, and a flag variable called swapped.

Join our Data Structures in C++ Free Course now and gain a competitive edge in your programming career!

Conclusion

• Bubble sort is a good and simple algorithm to sort a list.
• Good to use when memory space is limited.

Takeaways

• Bubble sort algorithm repeatedly compares the adjacent elements and swaps them if not in order.
• Complexity of bubble sort
  • Time complexity – O(n2n2)
  • Space complexity – O(1)