The Breadth First Search Algorithm is a cornerstone technique in computer science, renowned for its efficiency in traversing and searching tree or graph data structures. By exploring all neighbours of a node before moving to the next level, the BFS Algorithm ensures a thorough and level-wise exploration, making it indispensable for various applications, from networking to pathfinding.
What Is Graph Traversal Algorithms in Data Structure?
Graph traversal aims to systematically visit all vertices and edges in a graph without repeats. It includes:
- Breadth-First Search (BFS), which starts at a root node, explores all neighbors at the current depth, then proceeds to the next depth, using a queue for tracking. It’s ideal for finding shortest paths in unweighted graphs.
- Depth-First Search (DFS) delves deep into the graph, exploring each branch fully before backtracking, using a stack for path tracking. Useful for puzzles, topological sorting, and identifying connected components.
Both methods underpin many advanced algorithms and find applications across network analysis, pathfinding, and social media.
What is BFS Algorithm?
Breadth-First Search (BFS) is a crucial algorithm for graph traversal, prioritizing the exploration of a node’s immediate neighbors before advancing to their next-level neighbors. This strategy enables efficient searching for the shortest paths in unweighted graphs and ensures all nodes are visited systematically, starting from the closest. Employing a FIFO queue, BFS initiates from a chosen source node, exploring and marking each node by visiting adjacent unvisited ones, adding them to the queue for subsequent exploration. This process continues until the queue empties, signifying the completion of traversal.
The key to BFS is its FIFO queue usage, which facilitates node visits in their discovery order. This attribute makes BFS ideal for shortest path searches by edge count, calculating node levels from the source, or exhaustive visits within a graph’s connected component. Its structured, level-by-level approach ensures comprehensive coverage, making it indispensable for various graph-related operations.
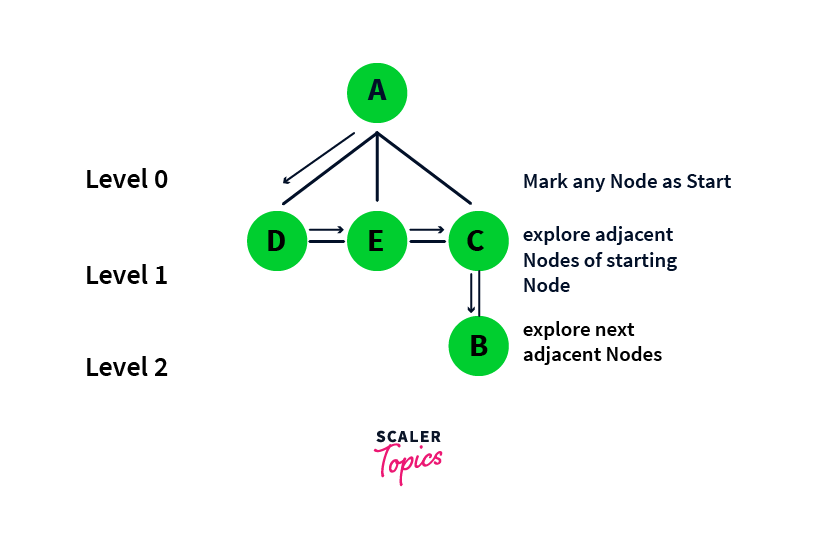
How Does the BFS Algorithm Works?
Beginning with the root node, the algorithm visits every node on a specific level before proceeding to the nodes on the subsequent level, continuing this pattern until it has visited all nodes.
This process utilizes a queue. It pushes all neighboring, unvisited nodes of the current level into the queue, marks the nodes of the current level as visited, and then removes them from the queue.
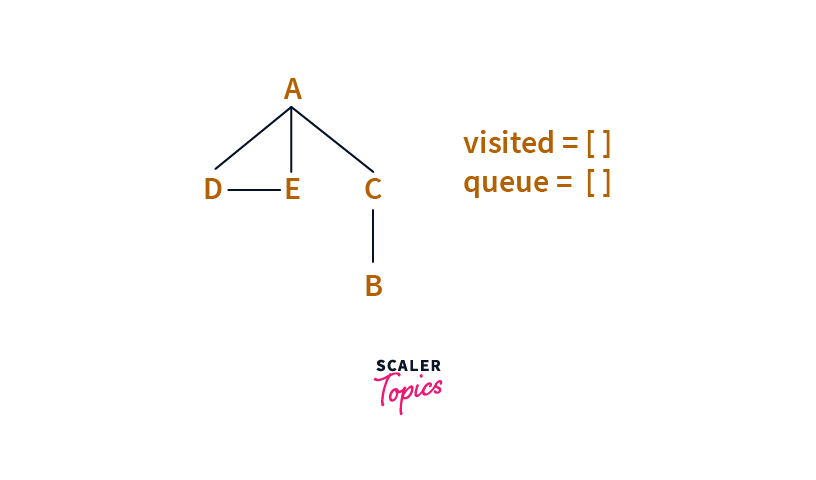
Let’s see how to use a Breadth-First Search from Node A.
We need to use two data structures a Queue (for FIFO property) and a Set visited (to mark the visited nodes).
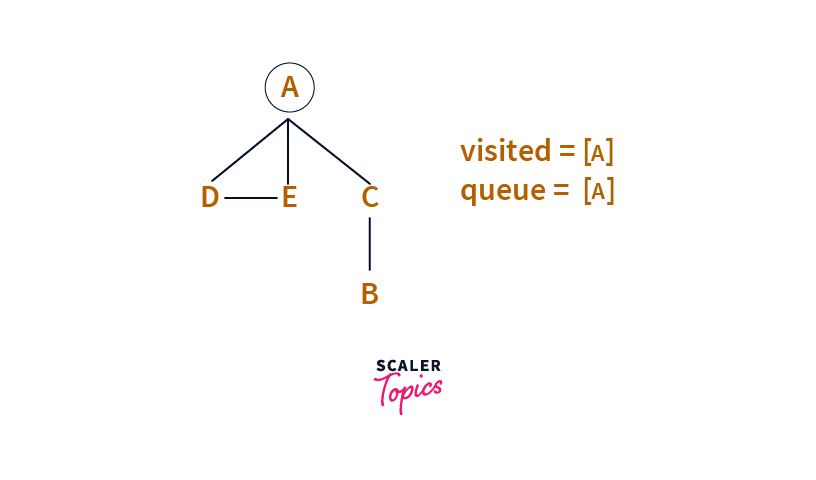
Step: 1
We pick A as the starting point and add A to the Queue. To prevent cycles, we also mark A as visited(by adding it to the visited set).
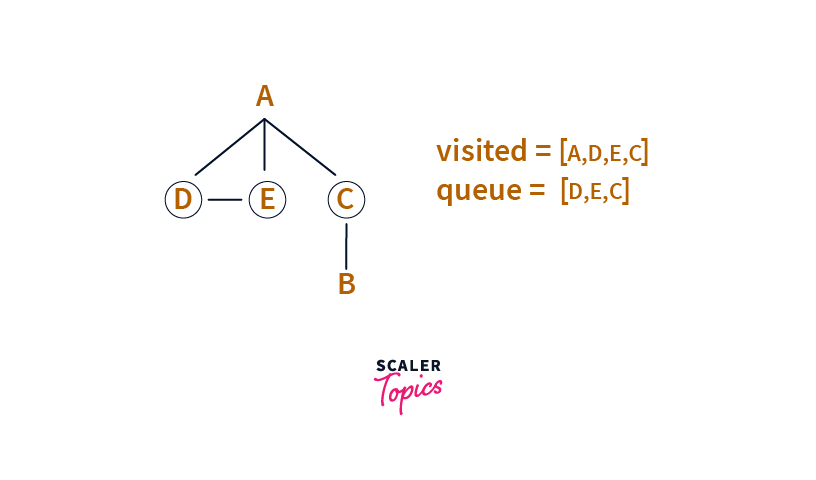
Step: 2
We remove the head of the Queue (i.e. A now). The Node was First In (inserted first) in the Queue.
We process A and pick all its neighbours that have not been visited yet(i.e., not in the visited set). Those are D, C, and E.
We add D, C, and E to the Queue and these to the visited set.
Step :3
Next, we pull the head of the Queue, , i.e. D.
We process D and consider all neighbours of D, which are A and E, but since both A and E are in the visited set, we ignore them and move forward.
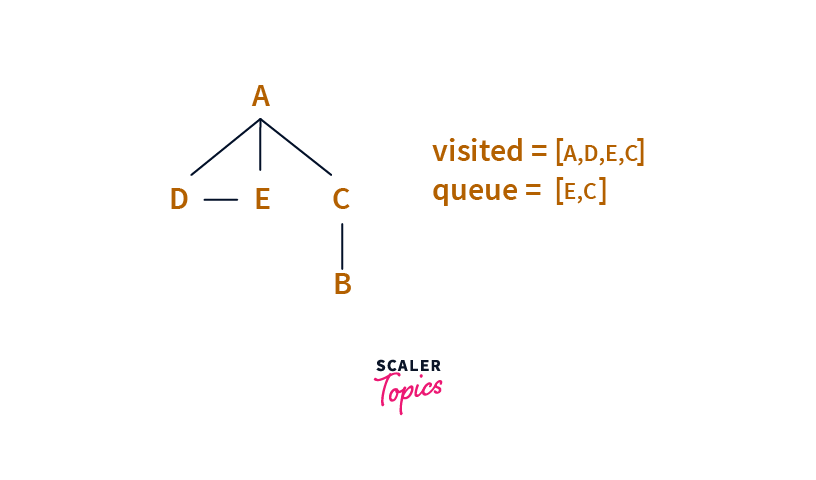
Step : 4
Next, we pull the head of the Queue, i.e. E.
We process E.
Then we need to consider all neighbours of E, which are A and D, but since both A and D are in the visited set, we ignore them and move forward.
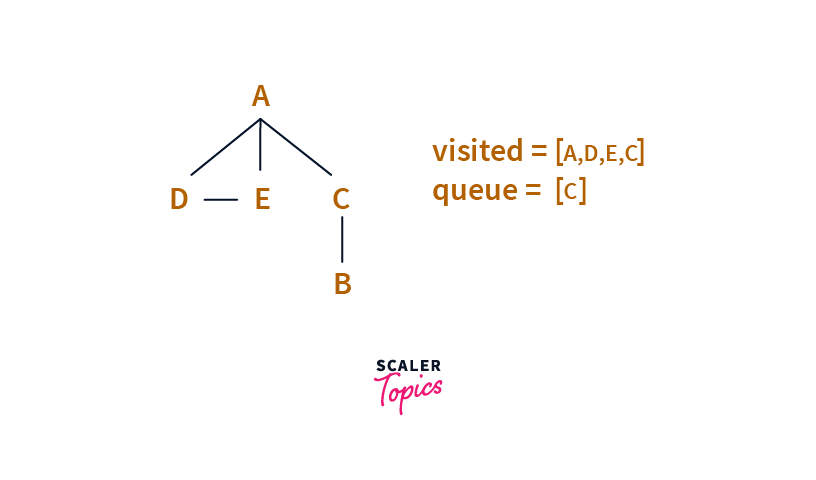
Next, we pull the head of the Queue, i.e. C.
We process C.
Then we consider all neighbours of C, which are A and B. Since A is in the visited set, we ignore it. But as B has not yet been visited, we visit B and add it to the Queue.
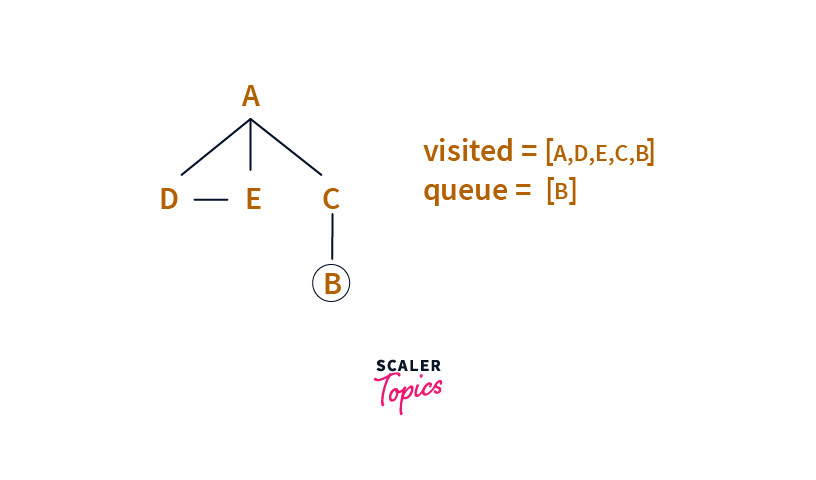
Step 5:
Finally, we pick B from Queue, and its neighbour is C, which has already visited. We have nothing else in Queue to process, so we are done traversing the graph.
So the order in which we processed/explored the elements are: A, D, E, C, B which is the Breadth-First Search of the above Graph.
So we see that the Breadth-First Search relies on 2 other data structures i.e. A queue and a Visited Set (or Arrays).
Queue ensures that we process elements in the order they were first seen, and Set(or Arrays) can be used to identify which elements have already been visited.
Pseudocode of Breadth-First Search
Create a Queue (say Q)
Mark Vertex V as Visited.
Put V into the Queue
While Q is not empty
Remove the head of Q (Let it be Vertex U)
Iterate all Unvisited Neighbours of U
Mark the neighbour as Visited
Enqueue the Neighbour into Q.Implementation of BFS Algorithm
Java Implementation
import java.util.*;
// This class represents an undirected graph using adjacency list representation
class Graph {
private int numberOfVertices;
private LinkedList<Integer> adjacencyList[];
Graph(int numberOfVertices) {
this.numberOfVertices = numberOfVertices;
adjacencyList = new LinkedList[numberOfVertices];
for (int i = 0; i < numberOfVertices; ++i)
adjacencyList[i] = new LinkedList<>();
}
void addEdge(int from, int to) {
adjacencyList[from].add(to);
adjacencyList[to].add(from);
}
void bfsTraversal(int vertex) {
// Mark all the vertices as UNVISITED (By default set as false).
boolean[] visited = new boolean[numberOfVertices];
// Create a queue for BFS
LinkedList<Integer> queue = new LinkedList<>();
visited[vertex] = true;
queue.add(vertex);
while (!queue.isEmpty()) {
vertex = queue.poll();
System.out.print(vertex + " ");
for (int n : adjacencyList[vertex]) {
if (!visited[n]) {
// If an adjacent Vertex has not been visited, then mark it visited and enqueue it
visited[n] = true;
queue.add(n);
}
}
}
}
public static void main(String args[]) {
Graph graph = new Graph(7);
graph.addEdge(0, 1);
graph.addEdge(0, 2);
graph.addEdge(1, 3);
graph.addEdge(1, 4);
graph.addEdge(2, 1);
graph.addEdge(2, 5);
graph.addEdge(3, 6);
System.out.println("Breadth First Traversal from 1 is:");
graph.bfsTraversal(1);
}
}Output:
Breadth-First Traversal from 1 is:
1 0 3 4 2 6 5C++ Implementation
#include<iostream>
#include <list>
using namespace std;
// This class represents an undirected graph using adjacency list representation
class Graph
{
int numberOfVertices; // No. of vertices
// Pointer to an array containing adjacency lists
list<int> *adjacencyList;
public:
Graph(int numberOfVertices); // Constructor
void addEdge(int from, int to);
void bfsTraversal(int startingVertex);
};
Graph::Graph(int numberOfVertices)
{
this->numberOfVertices = numberOfVertices;
adjacencyList = new list<int>[numberOfVertices];
}
void Graph::addEdge(int v, int w)
{
adjacencyList[v].push_back(w);
adjacencyList[w].push_back(v);
}
void Graph::bfsTraversal(int vertex)
{
// Mark all the vertices as not visited
bool *visited = new bool[numberOfVertices];
for(int i = 0; i < numberOfVertices; i++)
visited[i] = false;
// Create a queue for bfsTraversal
list<int> queue;
visited[vertex] = true;
queue.push_back(vertex);
list<int>::iterator i;
while(!queue.empty())
{
// Dequeue a vertex from queue and print it
vertex = queue.front();
cout << vertex << " ";
queue.pop_front();
// If a adjacent vertex has not been visited, then mark it visited and enqueue it
for (i = adjacencyList[vertex].begin(); i != adjacencyList[vertex].end(); ++i)
{
if (!visited[*i])
{
visited[*i] = true;
queue.push_back(*i);
}
}
}
}
int main()
{
Graph graph(7);
graph.addEdge(0, 1);
graph.addEdge(0, 2);
graph.addEdge(1, 3);
graph.addEdge(1, 4);
graph.addEdge(2, 1);
graph.addEdge(2, 5);
graph.addEdge(3, 6);
cout << "Breadth First Traversal from 1 is : \n";
graph.bfsTraversal(1);
return 0;
}Output:
Breadth-First Traversal from 1 is:
1 0 3 4 2 6 5 Python Implementation
from collections import defaultdict
# This class represents an undirected graph using adjacency list representation
class Graph:
# Constructor
def __init__(self):
# Default dictionary to store graph
self.graph = defaultdict(list)
# Function to add an edge to graph
def addEdge(self, v, w):
self.graph[v].append(w)
self.graph[w].append(v)
# Function to print a bfsTraversal of graph
def bfsTraversal(self, vertex):
# Mark all the vertices as not visited
visited = [False] * (max(self.graph) + 1)
# Create a queue for bfsTraversal
queue = []
# Mark the source node as
# visited and enqueue it
Queue.append(vertex)
visited[vertex] = True
while Queue:
# Dequeue a vertex from
# Queue and print it
vertex = Queue.pop(0)
print (vertex, end = " ")
# Get all adjacent vertices of the dequeued vertex vertex.
# If a adjacent has not been visited, then mark it visited and enqueue it
for i in self.graph[vertex]:
if visited[i] == False:
queue.append(i)
visited[i] = True
# Create a graph given
graph = Graph()
graph.addEdge(0, 1)
graph.addEdge(0, 2)
graph.addEdge(1, 3)
graph.addEdge(1, 4)
graph.addEdge(2, 1)
graph.addEdge(2, 5)
graph.addEdge(3, 6)
print ("Breadth First Traversal from 1 is : ")
graph.bfsTraversal(1)Output:
Breadth-First Traversal from 1 is:
1 0 3 4 2 6 5 Complexity of BFS Algorithm
From each V, we iterate all of the other neighbour vertices, i.e. at the other end of all of its edges, and the total edges we can have in the graph is E.
Then it means Breadth-First Search works in O(E + V) time.
Since the Visited array and Queue can have a max size of V(equal to as many vertices), the overall space complexity will be O(V).
Applications of Breadth First Search (BFS) Algorithm
Let’s explore the various applications of Breadth-First Search:
- Creating minimum spanning trees for unweighted graphs: By utilizing Breadth-First Search, it’s possible to navigate from any selected starting point to another with the least number of edges. This concept is pivotal in constructing a minimum spanning tree that encapsulates the shortest paths covering all vertices.
- Peer-to-peer networks: Breadth-First Search aids in identifying a neighboring peer from any given peer within peer-to-peer networks.
- Search engine crawlers: To index the web, search engines employ Breadth-First Search to systematically visit and catalog web pages starting from a source page and progressing through linked pages.
- GPS navigation: For determining locations within a specific distance from a starting point, Breadth-First Search is employed to locate and explore neighboring areas up to a defined radius.
- Network broadcasting: In the process of broadcasting from a source, the identification and subsequent broadcasting to neighboring nodes are achieved through Breadth-First Search, continuing this pattern recursively.
- Pathfinding: Breadth-First Search is utilized to discover a route between two points by starting from one vertex and traversing until the other is reached. If the search exhausts all reachable vertices without finding the target, it indicates no available path.
- Identifying all accessible nodes from a specific vertex: In any graph, especially disconnected ones, all nodes accessible from a particular starting point can be determined through Breadth-First Search. The completion of this search marks certain vertices as visited, denoting all nodes that can be reached.
Conclusion:
- In the data structure, BFS examines nodes level by level, starting from the chosen root node, ensuring a thorough and systematic graph traversal.
- It is particularly adept at finding the shortest paths in unweighted graphs because it explores all nodes at one level before proceeding to the next.
- Using a queue data structure adheres to the First-In-First-Out (FIFO) principle, which is crucial for maintaining the order of node exploration.
- BFS is employed in many applications such as networking, AI, pathfinding, and more, demonstrating its adaptability and importance.
- With a time complexity of O(V + E) for traversing a graph made up of V vertices and E edges, BFS is computationally efficient.