The heap is a tree-based structure that is a complete binary tree. The binomial tree is of orders 0 and 1. A binomial heap is a specific implementation of a heap. It is a collection of small binomial heaps that are linked to each other and follow the heap property. There should be at least one binomial tree in the binomial heap. It is mainly used to implement the priority queue.
Scope
- In this article, we will discuss the heap (max heap and min heap), the binomial heap, the binomial tree, and their properties.
- We will discuss the examples and implementation of binomial heaps.
- After that, we will talk about the major operations that will be performed in the binomial heap, like union, insertion, deletion, and so on.
Introduction to Heap
- The heap is a tree-based structure in which the nodes are present in a specific order. The total number of child nodes present in the node depends on the type of heap.
- The most commonly used heap is the binary heap, in which the node has at most
2children. The height of a binary heap islog2N, where N is the number of nodes.
The heap should have any of the following properties:
- Max Heap Property: The value present at the root node must be greater than the value present in the child node, this property should be followed for all the subtrees. The root node value is the largest among all the node values. A[Parent(i)] >= A[I]
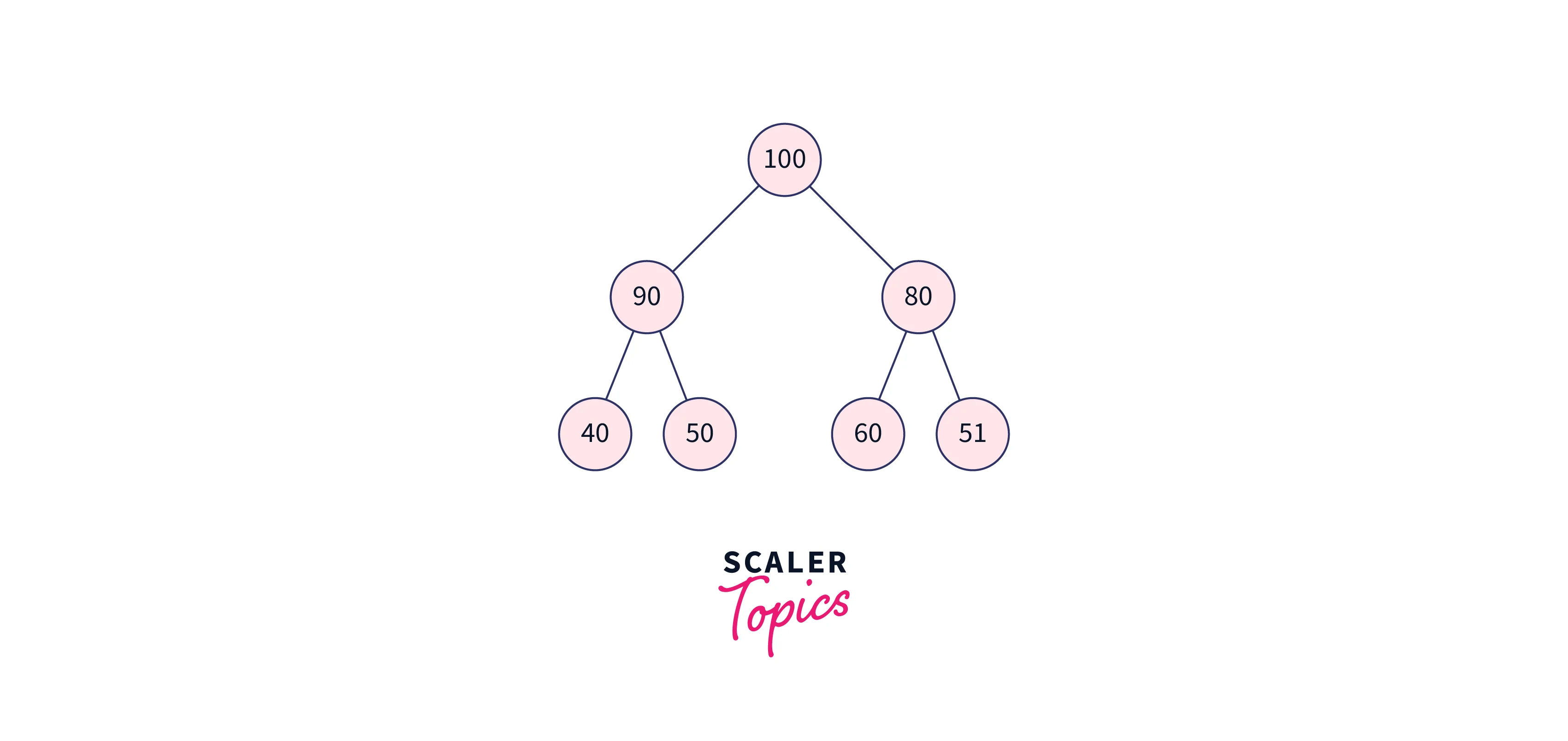
From the above figure, we can see that all the parents are smaller than their children, so this is the max heap.
- $5(Parent) < 10(Child) and 5(Parent)<15(Child)$
- $10(Parent) < 20(Child) and 10(Parent) < 30(Child)$
- $15(Parent) < 40(Child) and 15(Parent) < 50(Child)$
In the first point, 5 is a parent of 15 and 10, and it is smaller than both of its children. Similarly, for the other parents also.
- Min Heap Property:
The value present at the root node must be smaller than the value present in the child node, this property should be followed for all the subtrees. The root node value is the smallest of all the node values. A[Parent(i)] <= A[I]
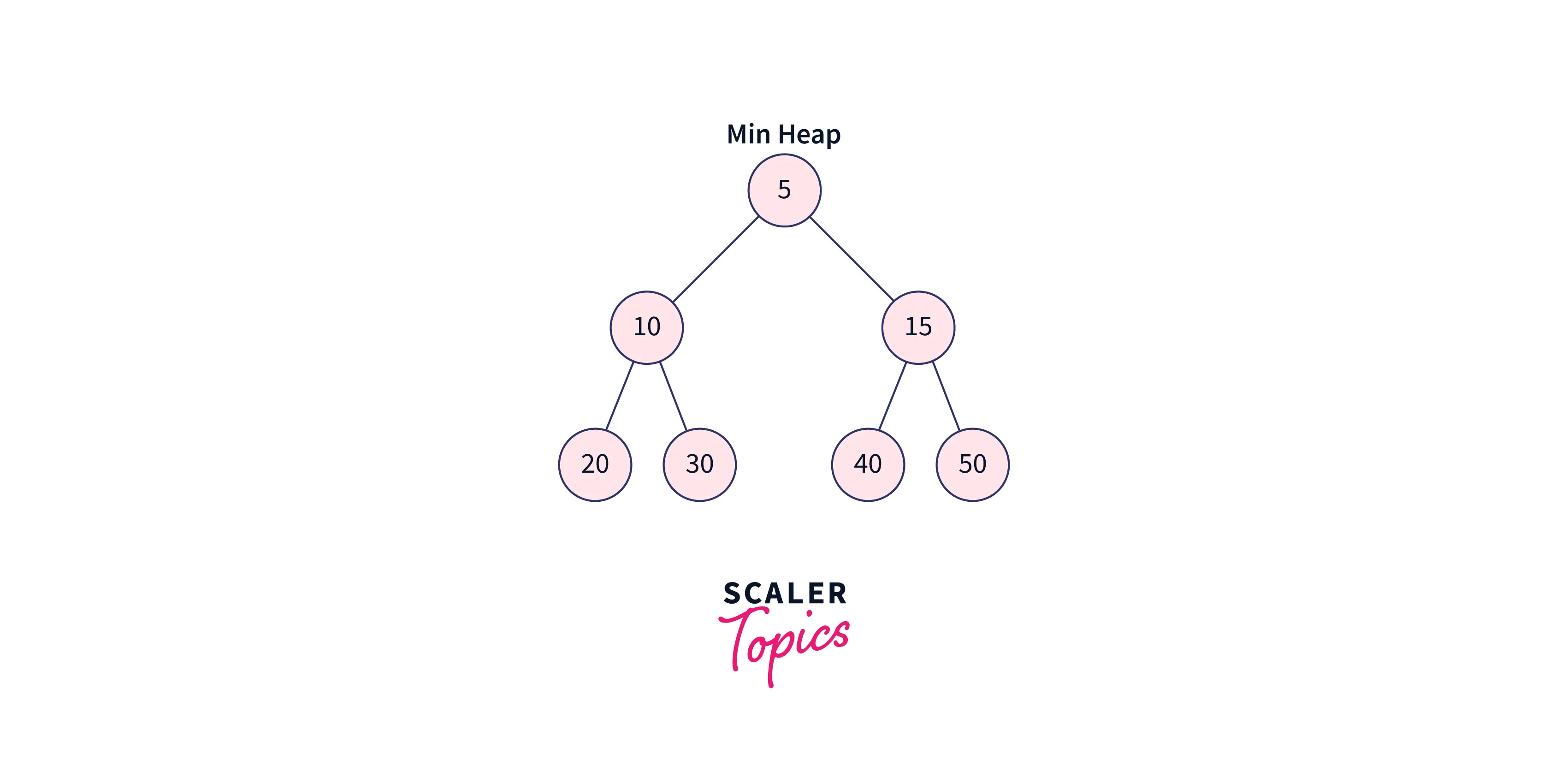
From the above figure, we can see that all the parents are greater than their children, so this is the min heap.
In the first point, 100 is a parent of 90 and 80, and it is greater than both of its children. Similarly, for the other parents also.
What is a Binomial Tree?
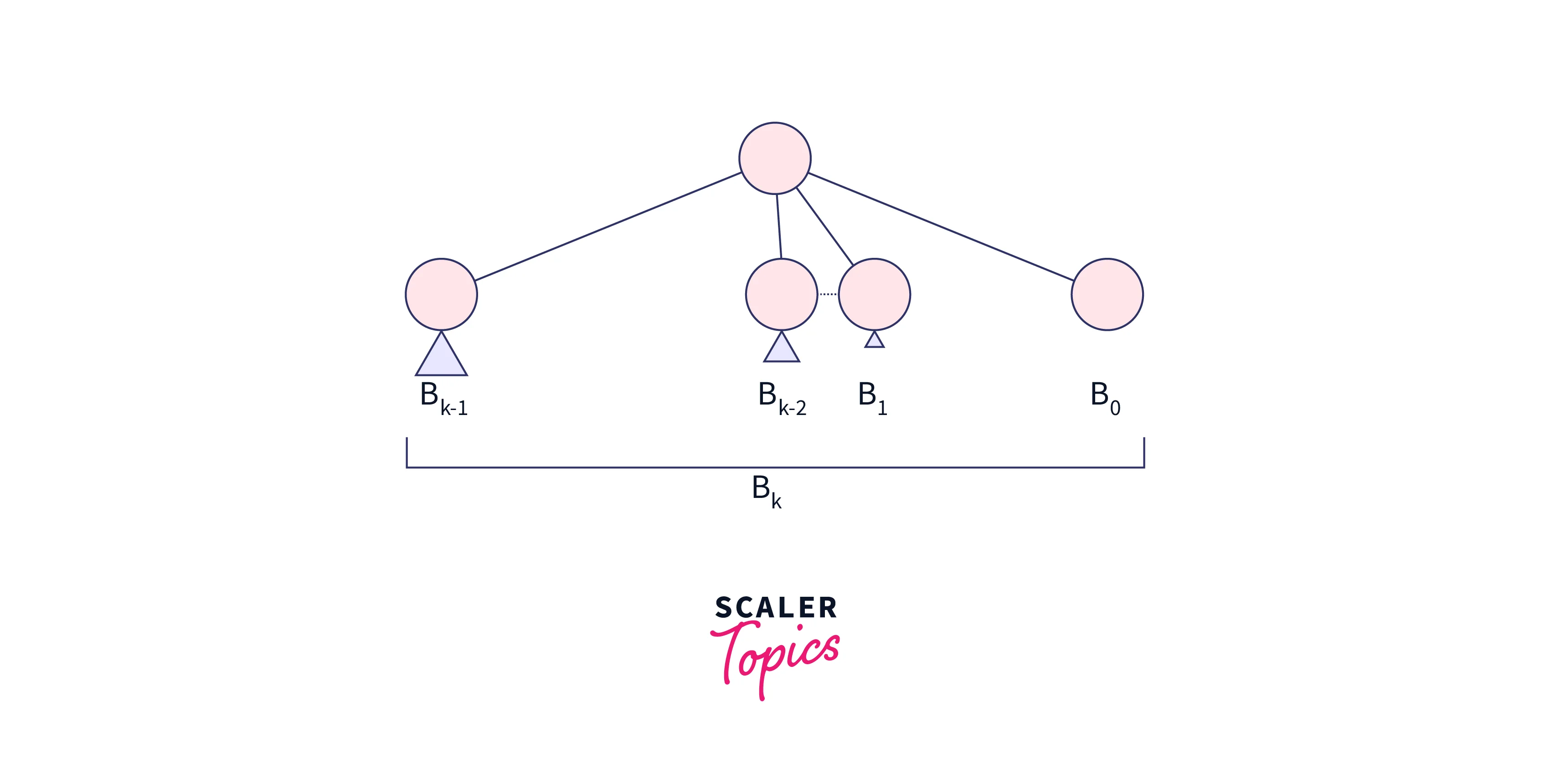
The Binomial tree Bk is the ordered tree made of linking two binomial trees, Bk-1 in which one becomes the leftmost child or the other. The number of nodes the zero-order binomial tree has is 1.
Some properties of the binomial tree are:
- It has $2^k$ number of nodes where k is the order.
- The tree has a depth equal to k.
- The children of the root, which has order k, are also binomial trees with orders k-1, k-2, and 0 from left to right.
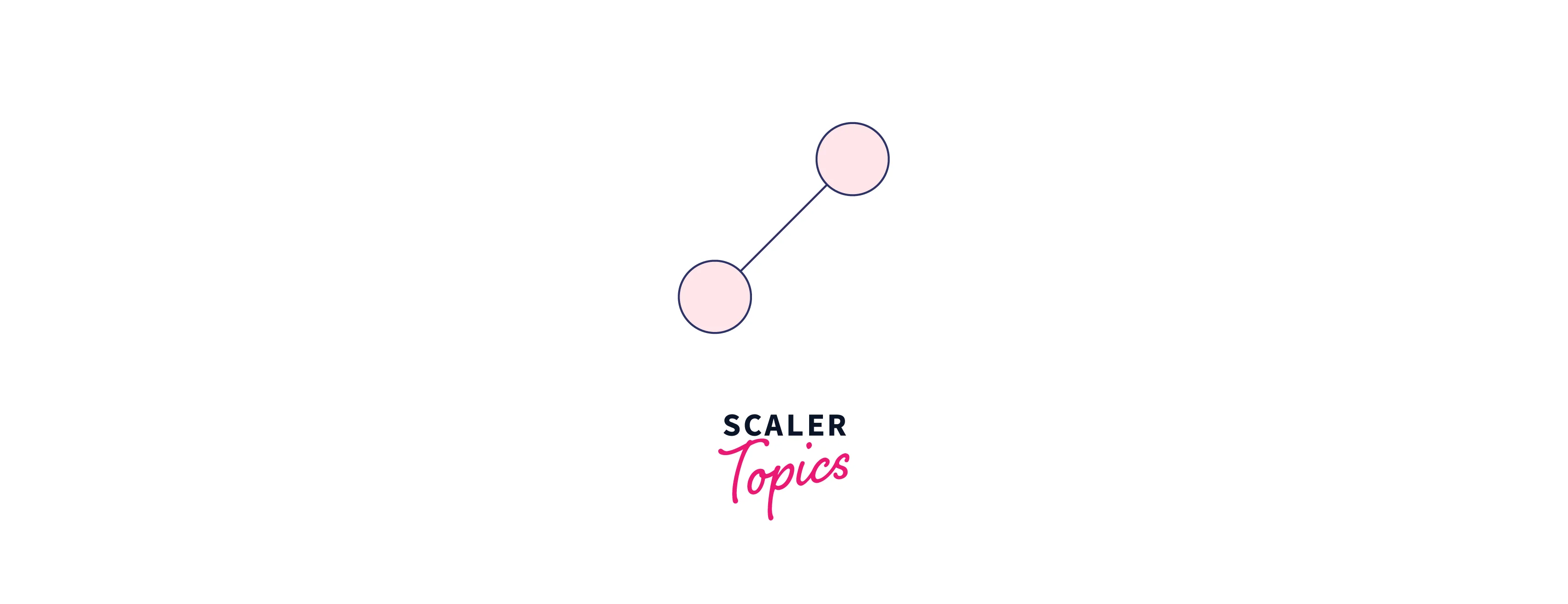
Step 1: For k = 0 (1 Node)

From the diagram, when the order (k = 0), only one node is present.
Step 2: For k = 1(2 Nodes)
The binomial tree of order 1 (k = 1) is formed by the two binomial trees of order zero (k = 0). One becomes the child of the other.
Step 3: For k = 2 (4 Nodes)
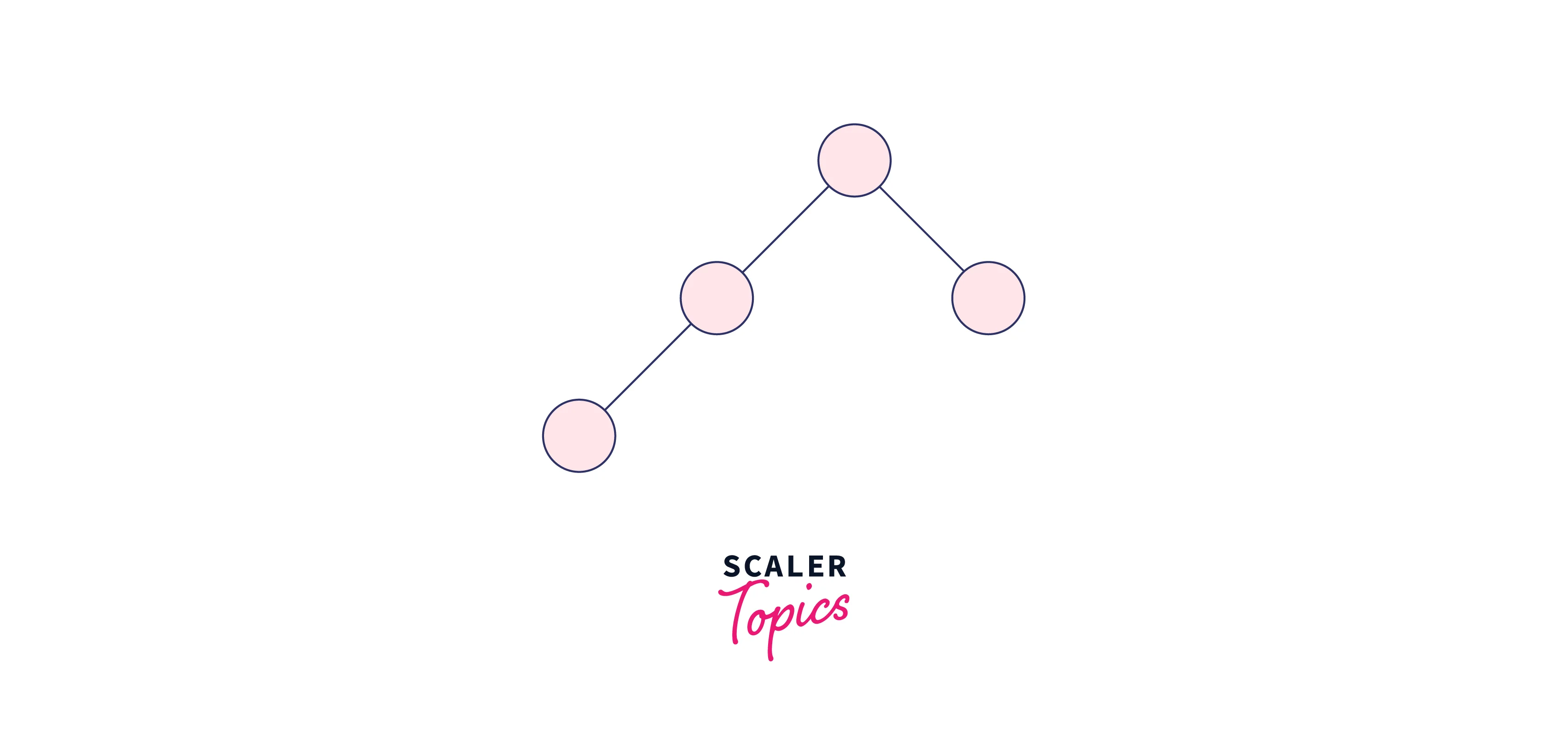
The binomial tree of order 2 (k = 2) is formed by the two binomial trees of order zero (k = 1). One becomes the child of the other.
Step 4: For k = 3(8 Nodes)
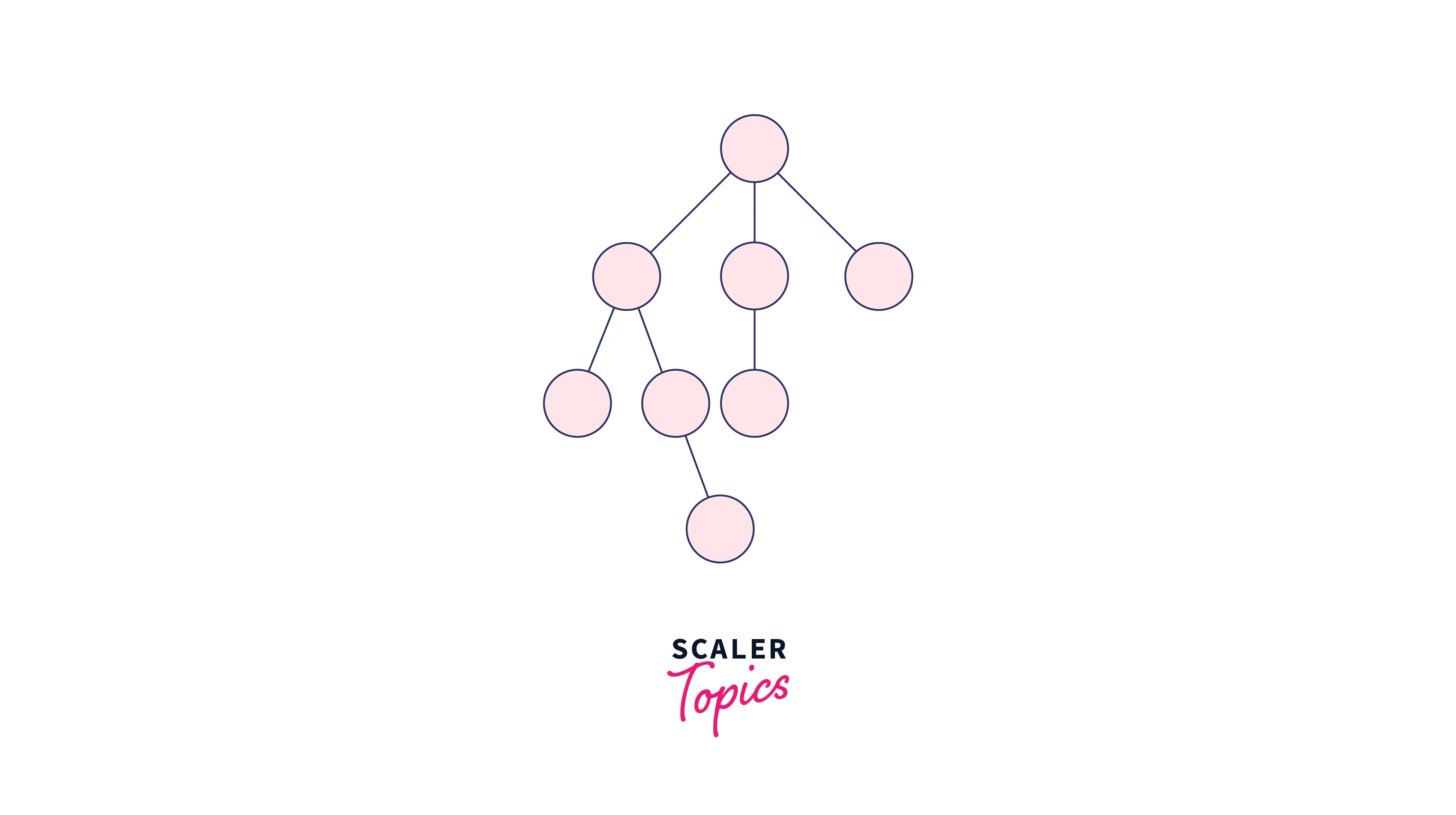
The binomial tree of order 3 (k = 3) is formed by the two binomial trees of order zero (k = 2). One becomes the child of the other.
Introduction to Binomial Heap
A binomial heap is a collection of binomial trees, each of which satisfies the heap property, i.e., the min-heap property. Each binomial tree is in heap order. So we can say the key of the node is greater than or equal to the key of its parent. There can be at most one binomial tree of any degree.
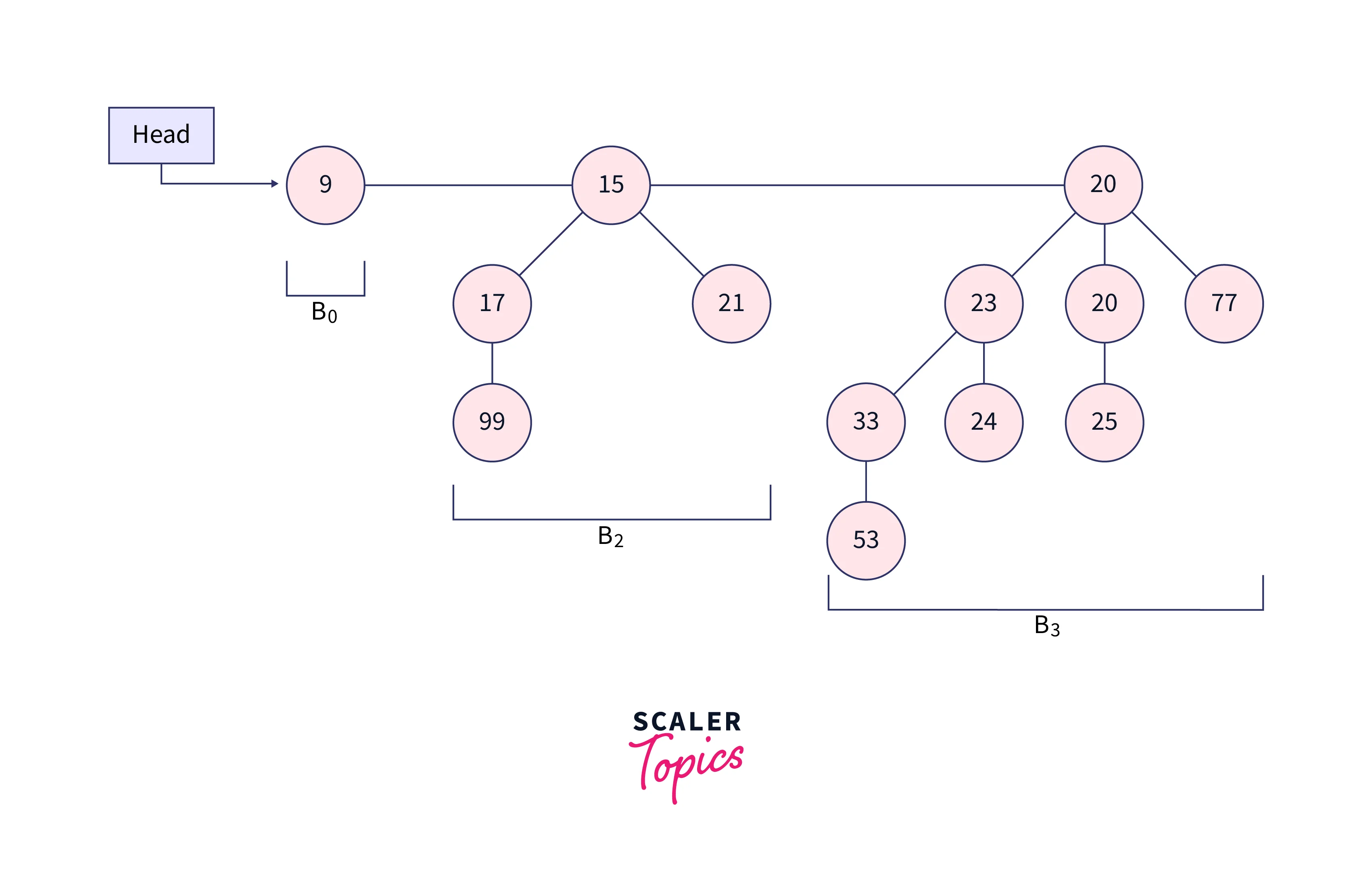
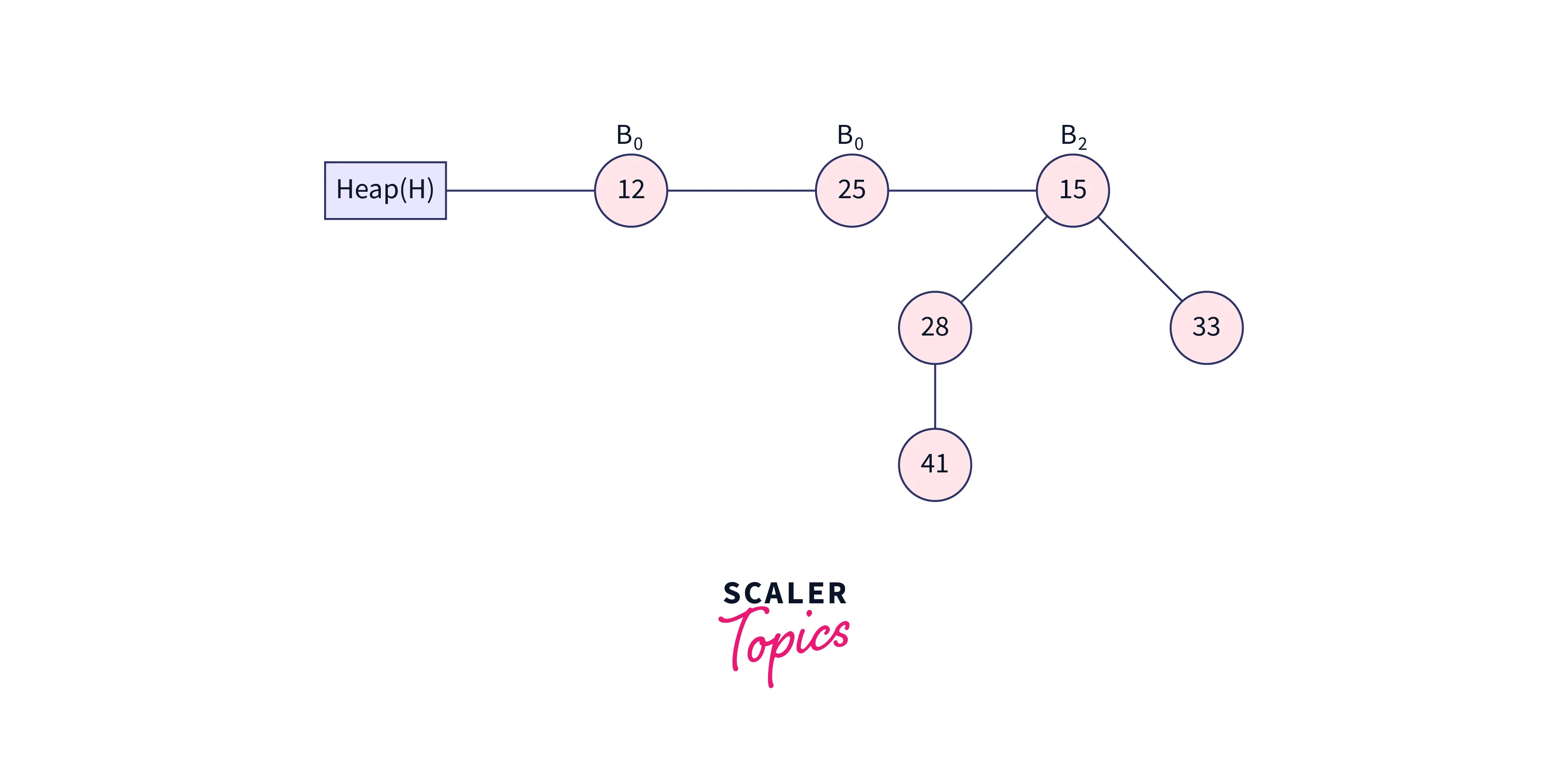
From the given fig, we can say that it consists of binomial trees B0, B2, and B3, which have 1, 4, and 8 nodes, so there are a total of 13 nodes. The roots of binomial trees are linked in increasing order of their degree.
What are the Properties of Binomial Heap?
The binomial heap has n nodes that should follow these properties:
- Each binomial tree in the heap should follow the min-heap property, i.e, the value of the node is greater than or equal to the value of its parent.
- At least one binomial tree should be in a heap where the root has a degree of k. where k can be any non-negative integer.
- First, ensure the min-heap property throughout the heap. The second property is that there should be a $1+log2n$ binomial tree where n is the number of nodes in the heap.
Example of Binomial Heap
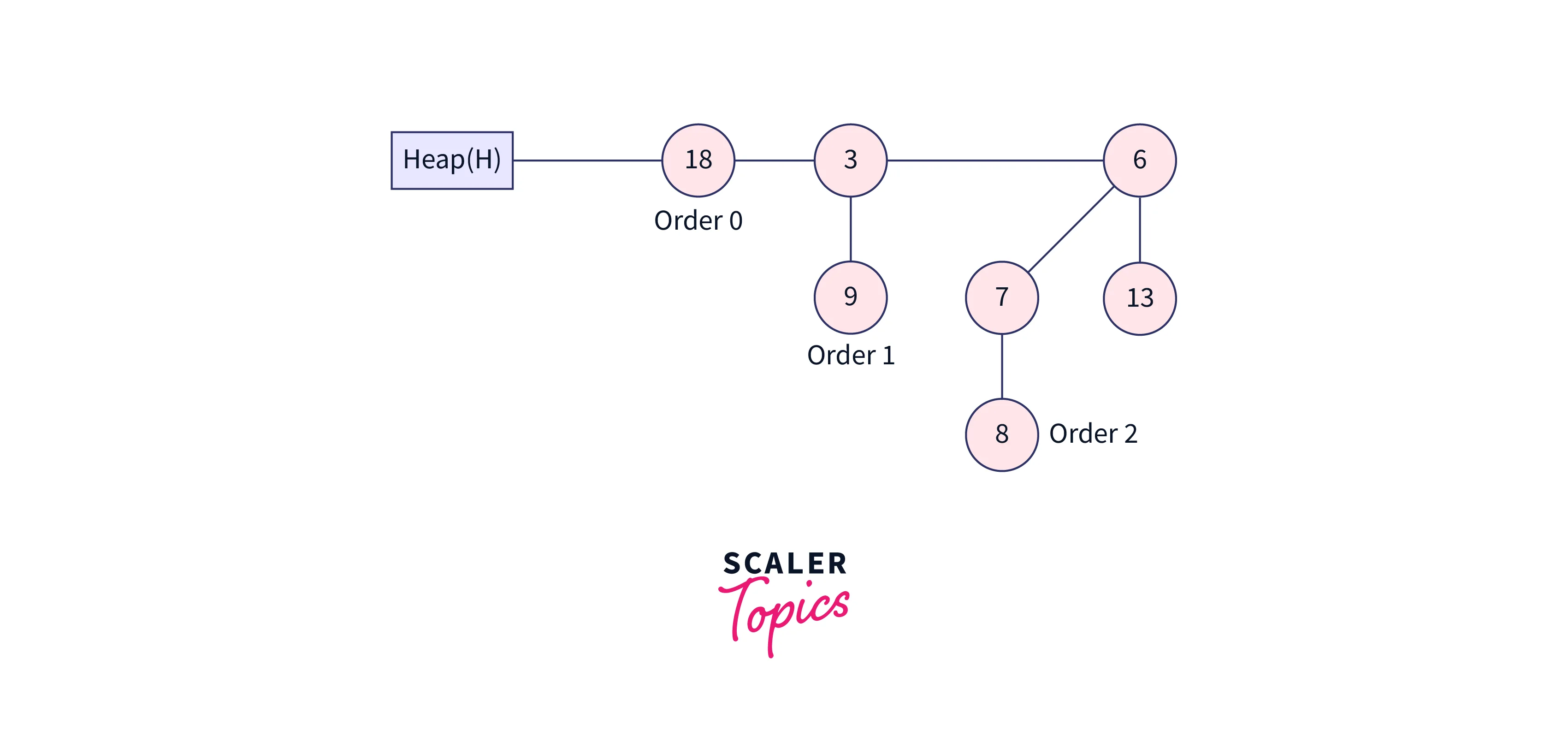
The above binomial heap has 13 nodes, i.e., it has the binomial tree B0, B2, and B3. The nodes in B0 are 1 node, B2 has 4 nodes, and B3 has 8 nodes. Each of the binomial trees follows the min-heap property.
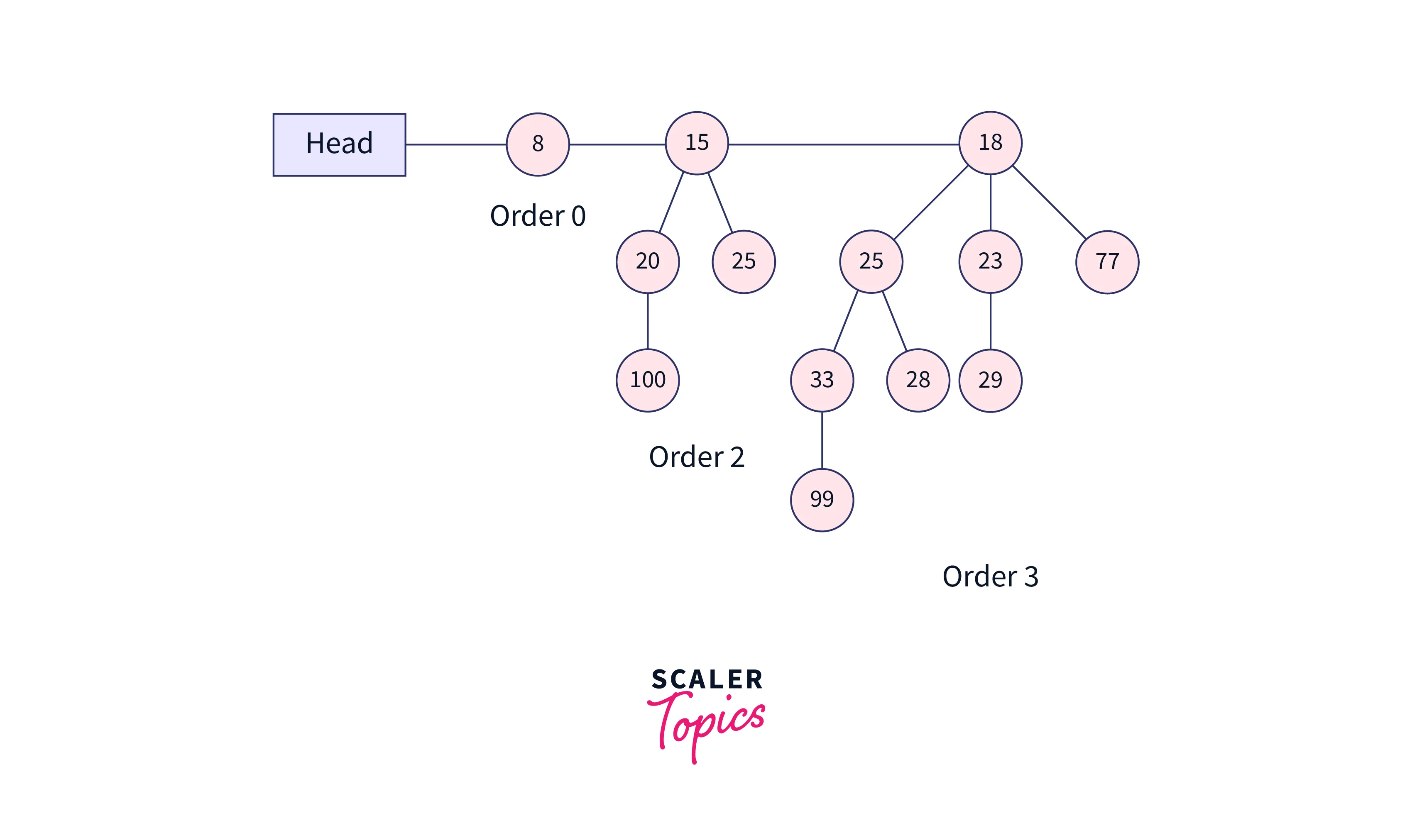
The above binomial heap has 7 nodes, i.e., it has the binomial tree B0, B1, B2. The nodes in B0 are 1 node, B1 has 4 nodes, and B2 have 8 nodes. Each of the binomial trees follows the min-heap property.
Binomial Heap and the Binary Representation of a Number
The binomial heap can be used to represent the binary number also, i.e., if the binomial heap has n binomial trees, where n is the number of set bits in the binary representation of the number.
If we want to create a binomial heap of n nodes, then it can be defined by the binary number ‘n’. Let us explain with a plethora of examples. If we want to create a binomial heap of 15 nodes, the binary representation of 15 is 1111, so now numbering from the right-hand side, the set bits are at positions 0,1,2,3. Therefore, the binomial heap will be formed with 15 nodes and the binomial tree B0, B1, B2, and B3.
Let’s try to understand with one more example. Suppose we want to create a binomial heap of 11 nodes. The binary representation of 11 is 1011, numbering from the right-hand side. The set bits are at 0, 1, and 3, so the binomial tree formed will be B0, B1, and B3. The degree of trees will be 0, 1, or 3 respectively.
Operations of Binomial Heap
The operations that could be performed in the binomial heap are given below:
- Creating a new binomial heap
- Finding the minimum key
- Union of two binomial heap
- Inserting a node
- Extracting minimum key
- Decreasing a key
- Deleting a node
Let’s discuss the above-listed operations one by one.
Creating a New Binomial Heap
Creating a new binomial heap simply takes O(1) because creating a heap will create the head of the heap to which no elements are attached.
Finding the Minimum Key
As previously stated, a binomial heap is a collection of binomial trees, and each binomial tree fulfills the min-heap property. It denotes that the root node has a minimum value. To find the minimum key, we simply compare the root nodes of all the binomial trees. In a binomial heap, the time complexity of finding the minimum key is O(logn).
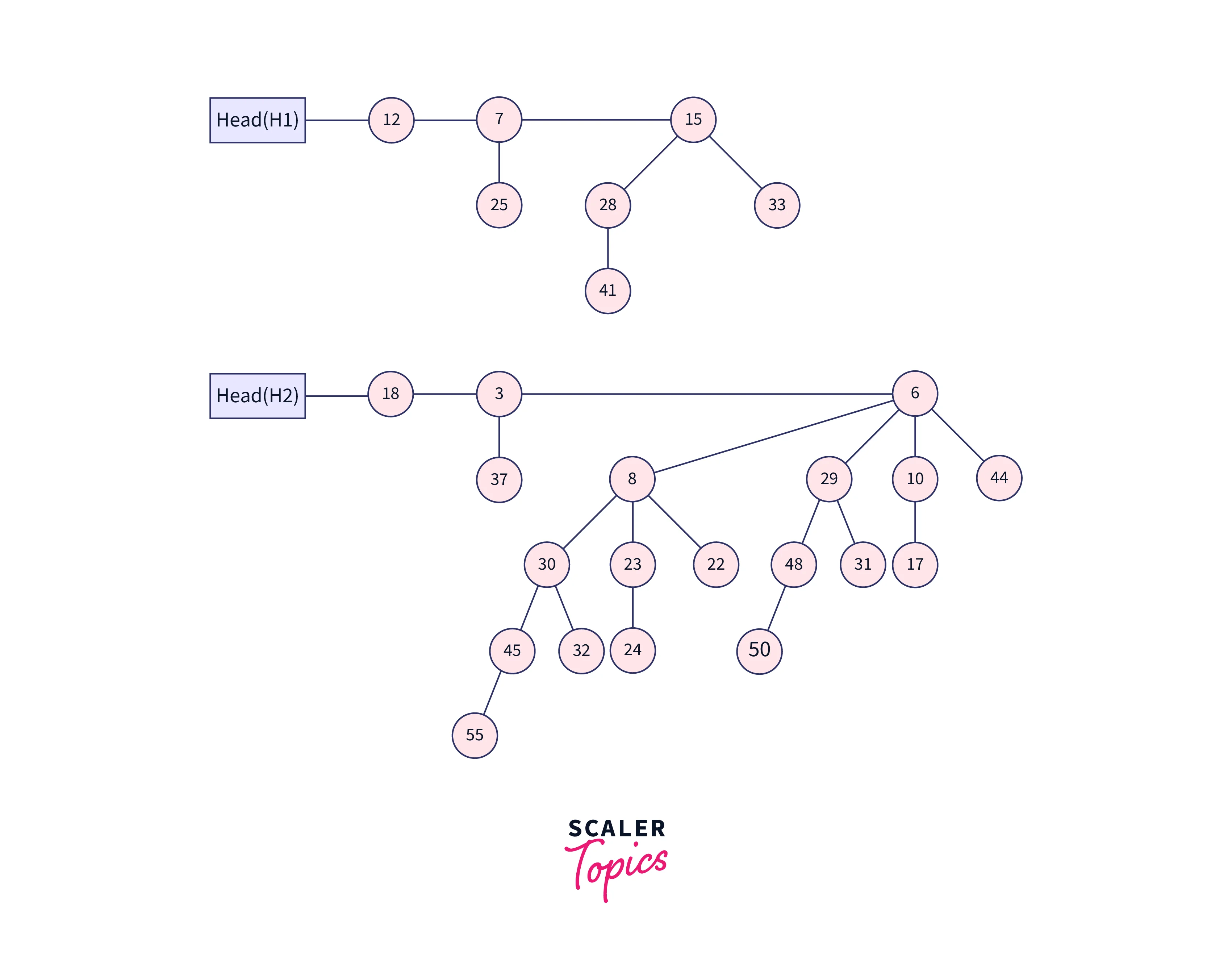
Union of Two Binomial Heap
- Union (H1, H2) combines two binomial heaps, H1 and H2, to form a single binomial heap.
- The first step is to merge the two heaps in a non-descending order of degrees.
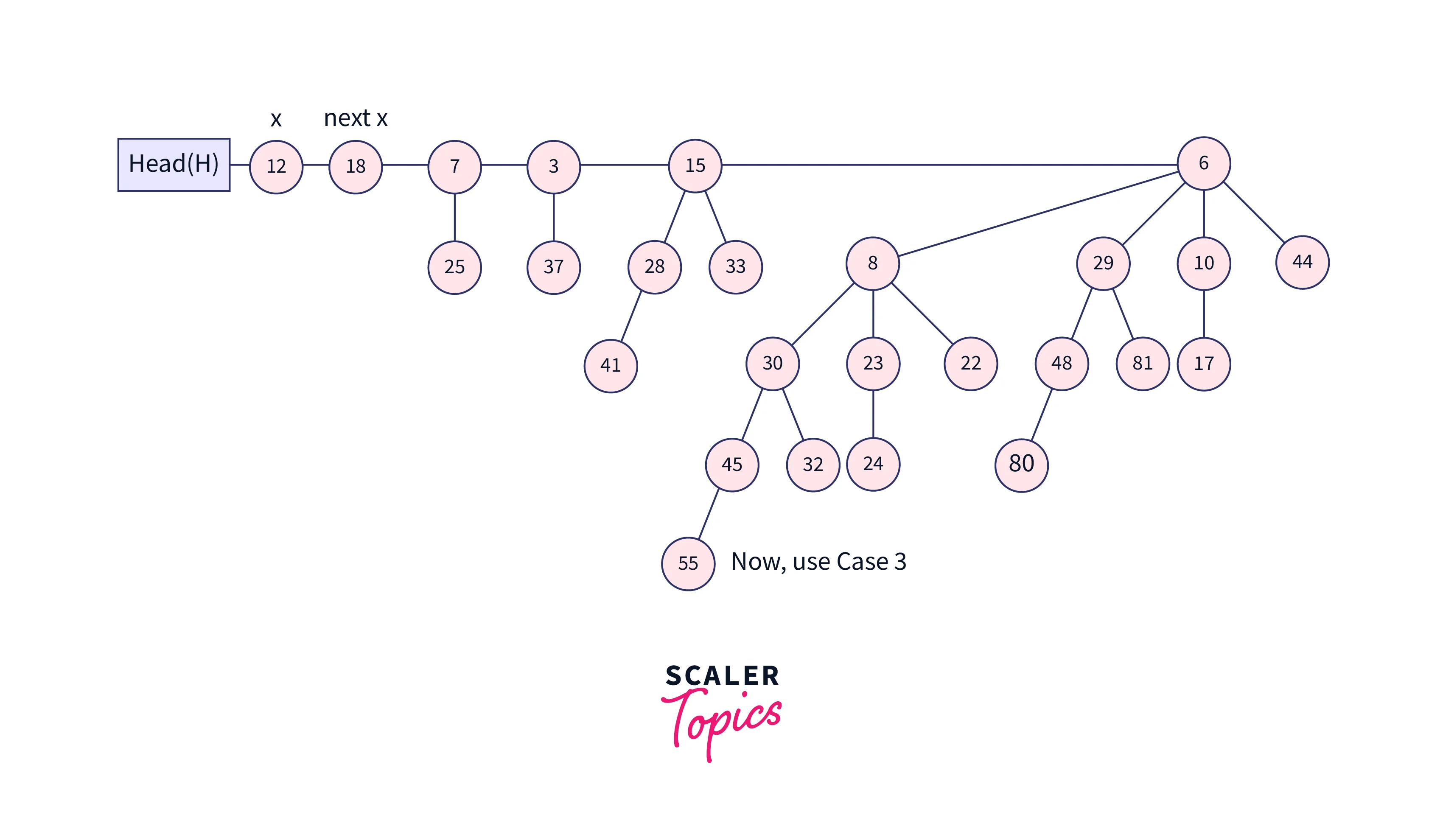
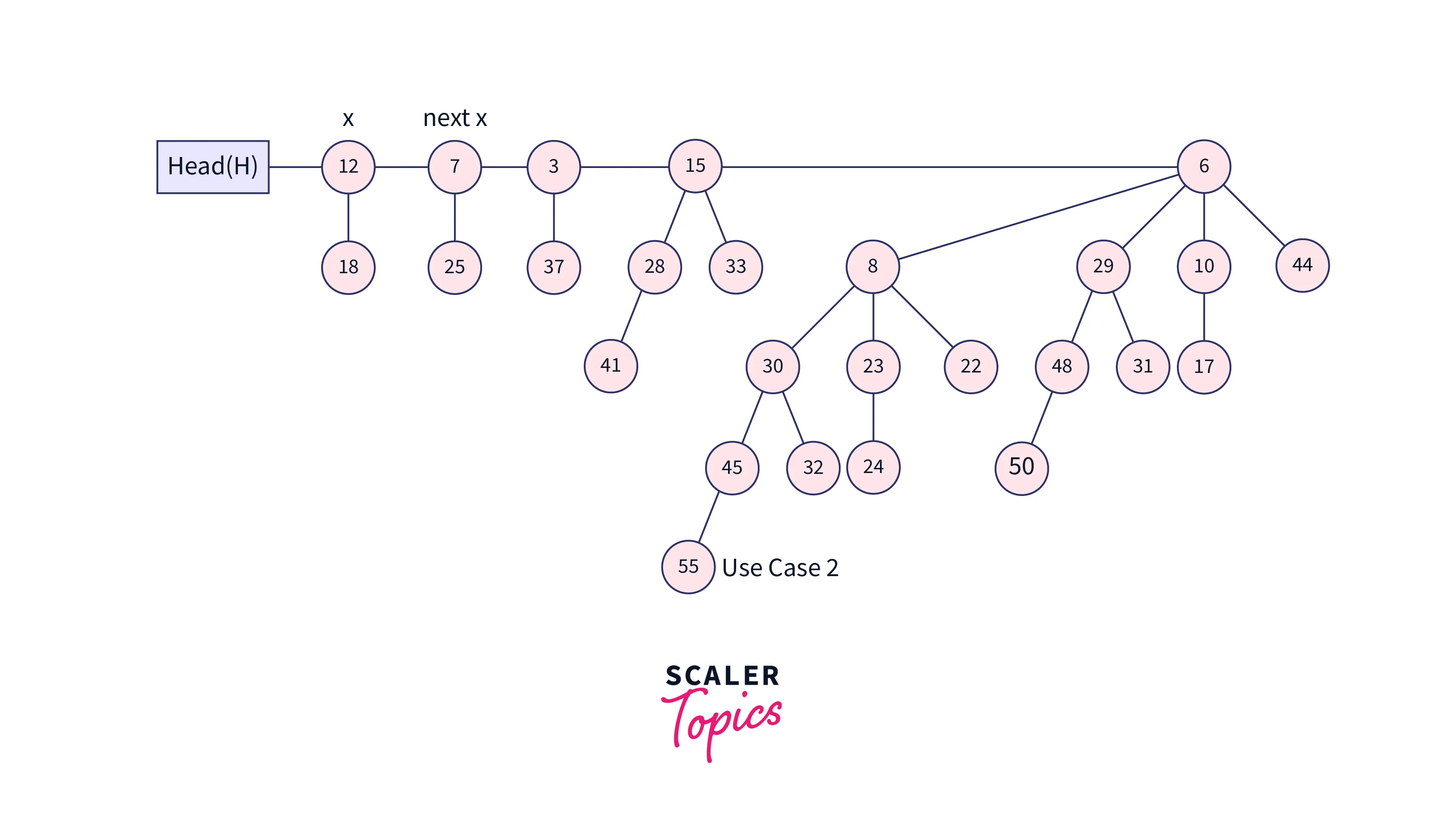
- After the simple merge, we must ensure that there is only one binomial tree of any order. To do this, we must combine binomial trees of the same order. We go through the list of merged roots, keeping track of three-pointers, previous, x, and next-x.
- When we traverse the list of roots, we may encounter the following four scenarios:
- Case 1: Because the orders of x and next-x do not match, we simply proceed.
In the three cases listed below, x and next-x are in the same order.
- Case 2: If the next-next-x order is the same, continue.
- Case 3: Link next-x to x if the key of x is lower than or equal to the key of next-x.
- Case 4: Make x the child of next if its key is greater.
Let’s understand all the above cases using a diagram.
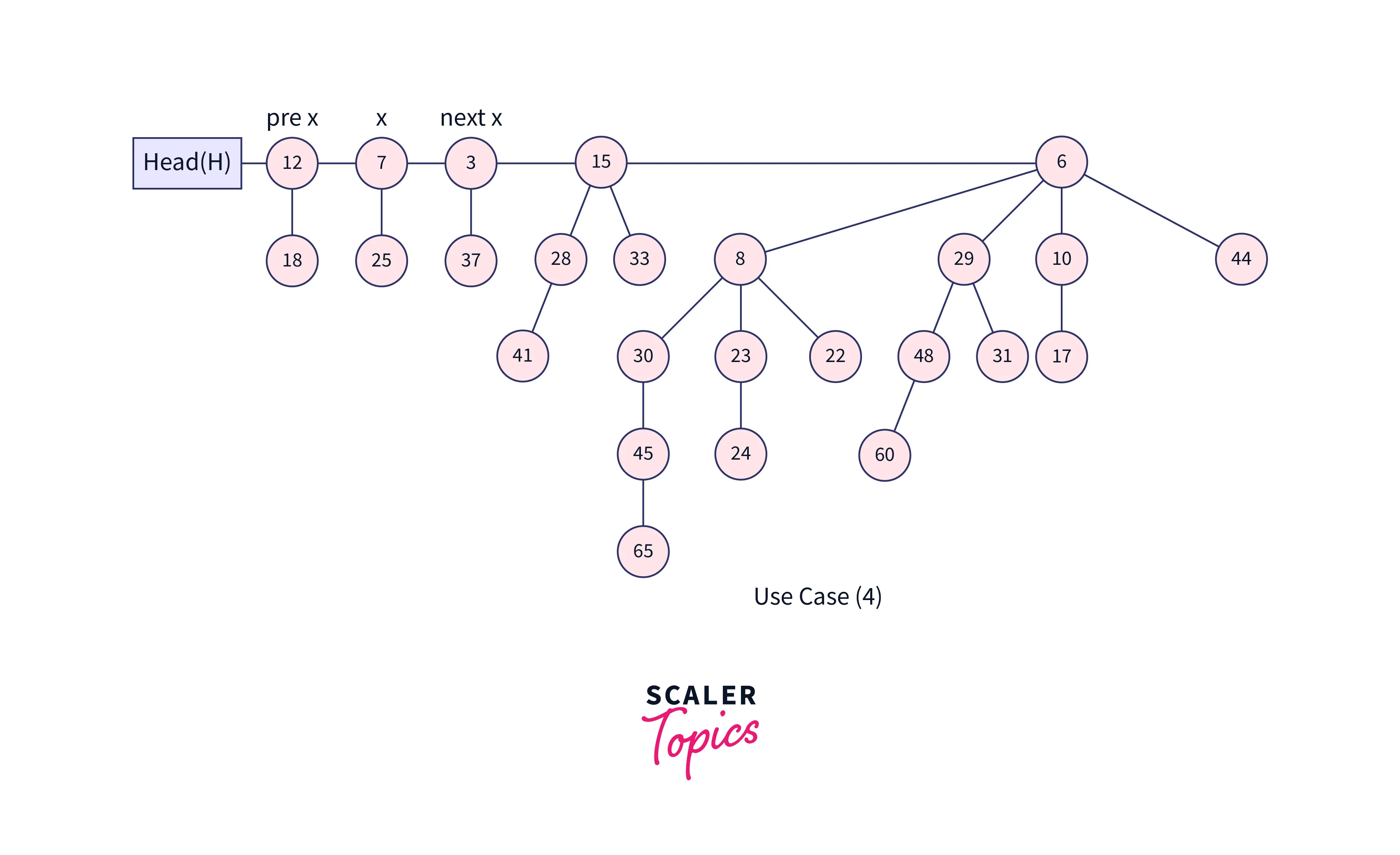
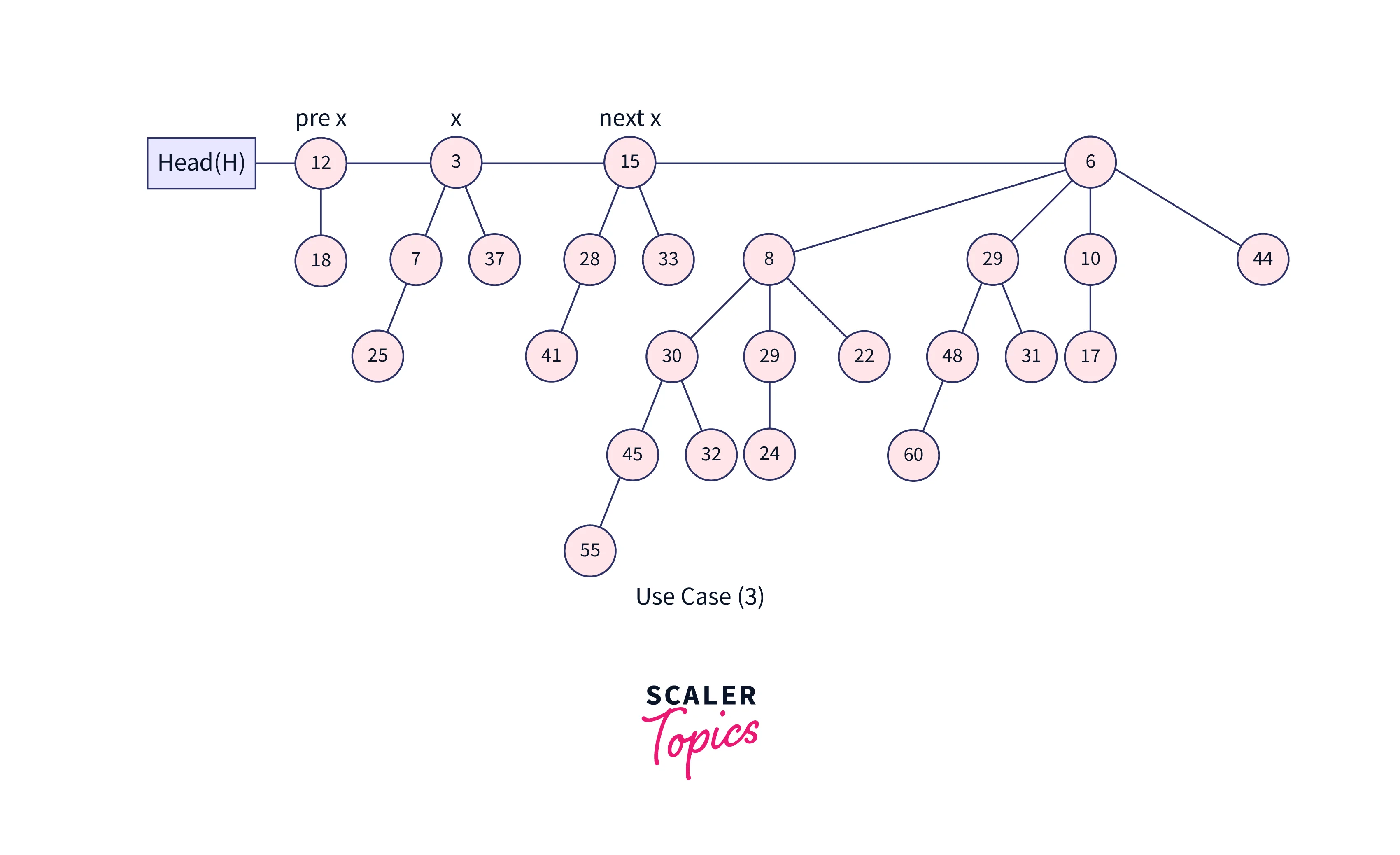
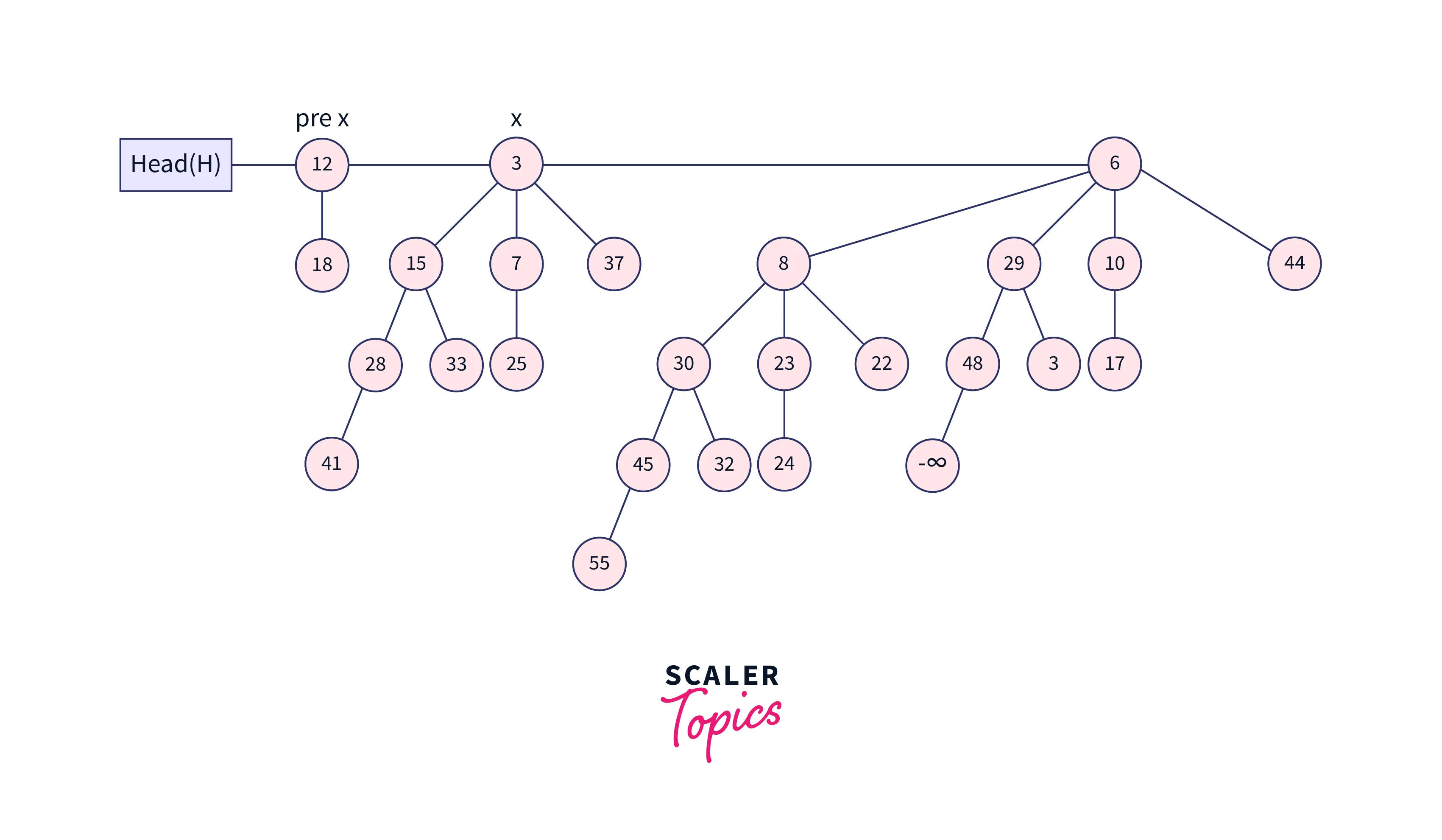
Inserting a node
It is possible to insert an element into the heap by simply creating a new heap that contains the element to be added and merging it with the existing heap. The time required for a single insertion into a heap after merging is $O(logn)$.
Let’s use an example to understand how to add a new node to a heap:
Three binomial trees of degrees 0, 1, and 2 are given in the heap above, with B0 attached to the top of the heap.
Let’s say we need to add node 15 to the heap mentioned above.
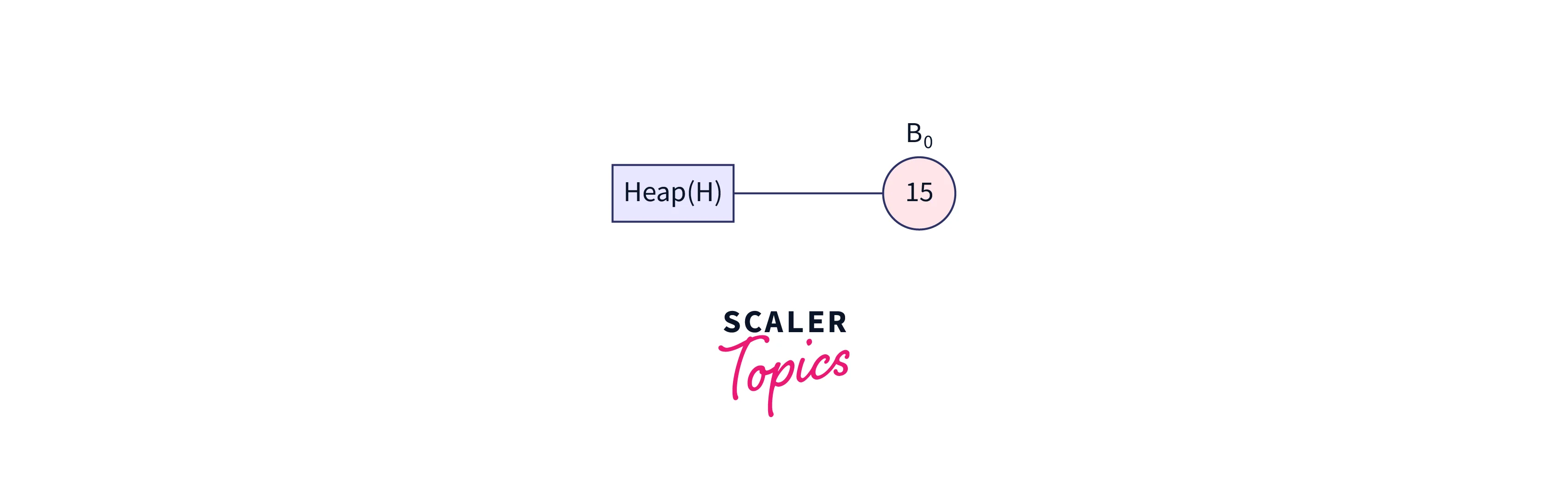
We must first combine the two heaps. Node 15 is connected to node 12 as shown below because both nodes 12 and 15 have a degree of 0.
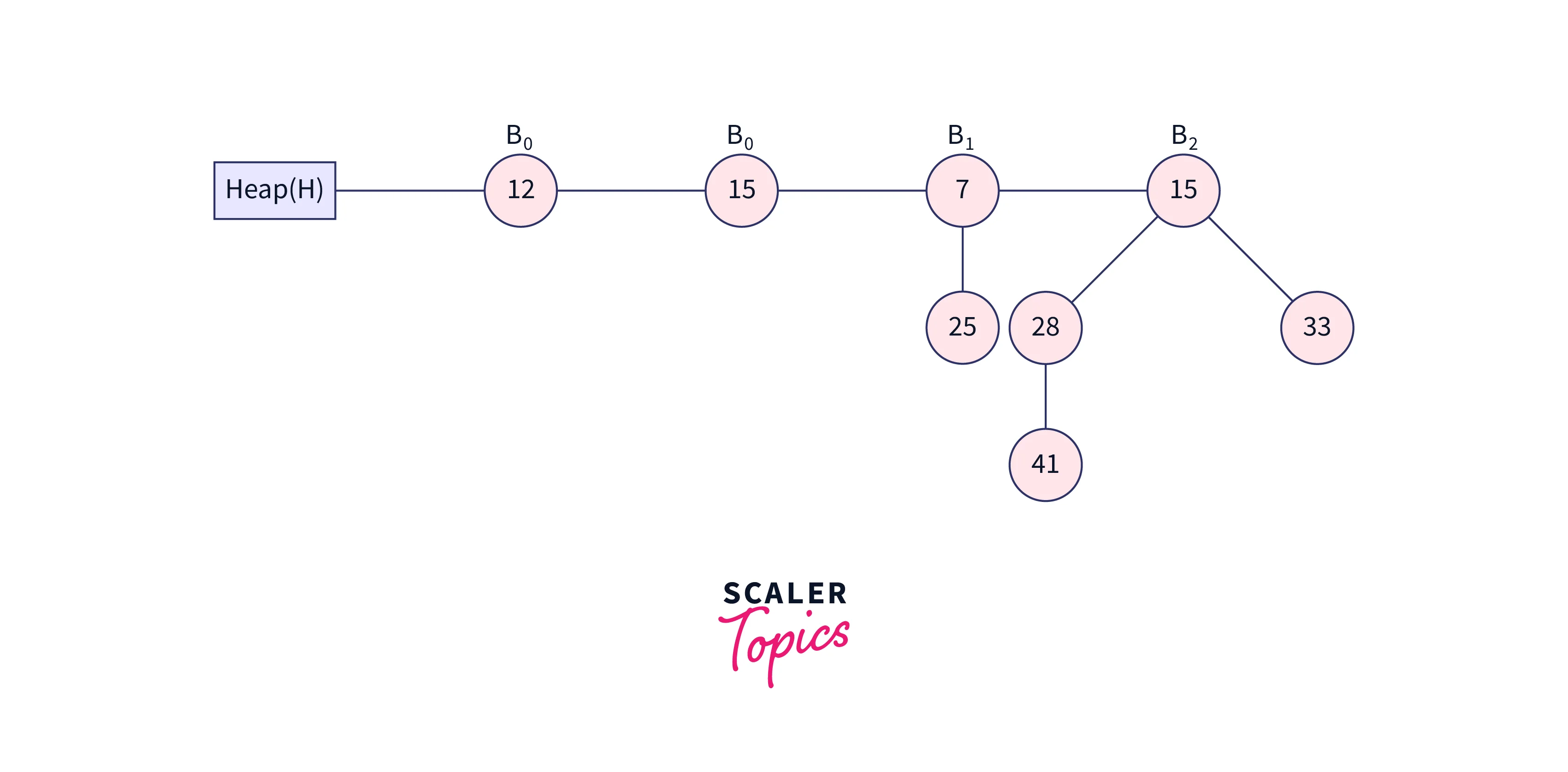
After that, assign x to B0 with a value of 12, next(x) to B0 with a value of 15, and sibling(next(x)) to B1 with a value of 7. Because x and next(x) have the same degree. Next(x) is dropped and attached to x because the key value of x is smaller than the key value of next(x). It can be seen in the picture below.
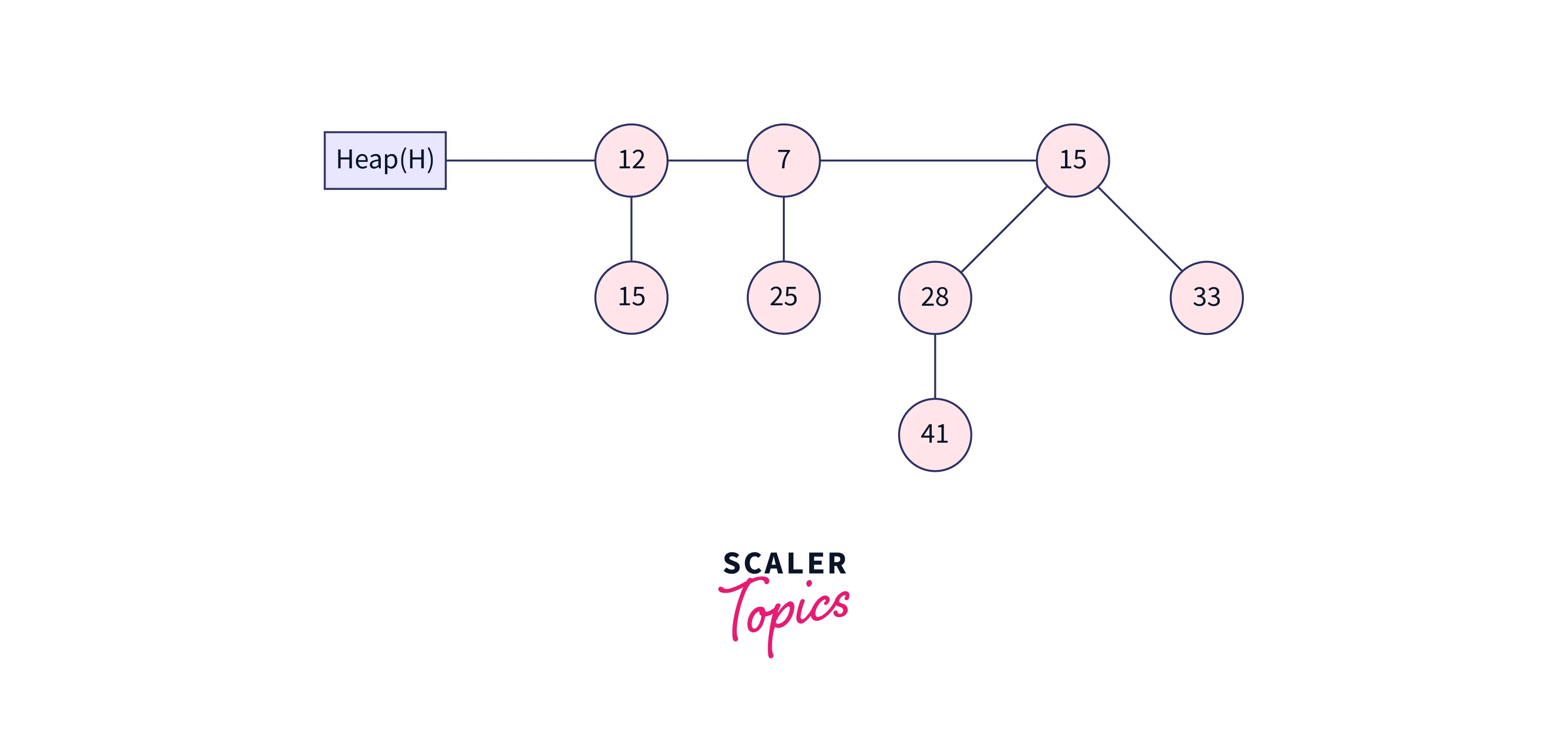
Currently, x points to node 12 with degree B1, followed by x to node 7 with degree B1, and sibling(next(x)) points to node 15 with degree B2. While x and next(x) have the same degree, sibling(next(x)) does not have the same degree as x. Since x’s, the key value exceeds that of next(x), x is eliminated and attached to next(x), as shown in the image below.
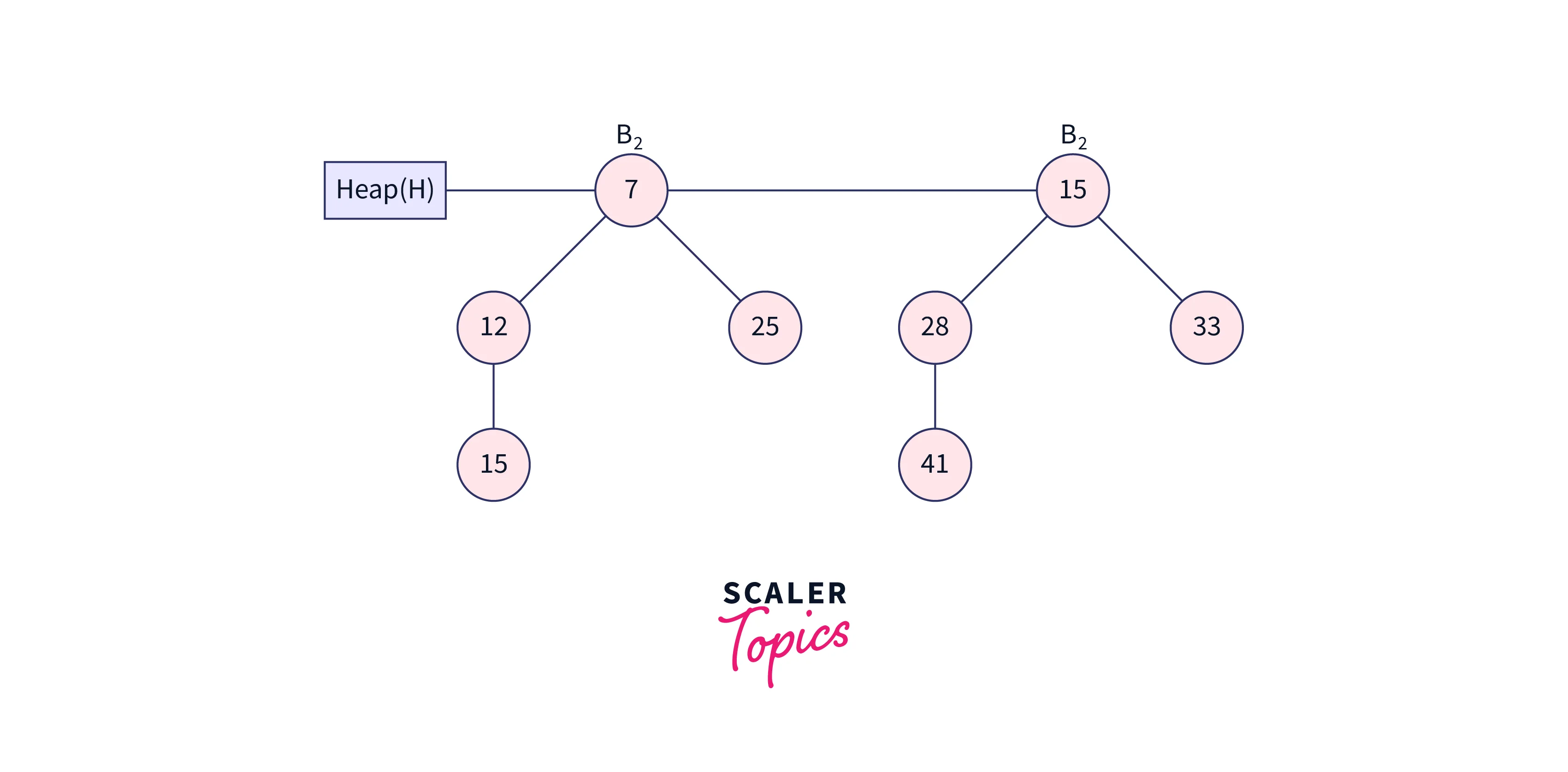
Right now, node 7 is pointed to by x, and node 15 is indicated by next(x). Since both x and next(x) have degrees of B2, and x’s key value is lower than next(xkey )’s value, next(x) will be taken out and attached to x as shown in the illustration below.
The final binomial heap after inserting node 15 has a degree of B3 and is described above.
Extracting Minimum Key
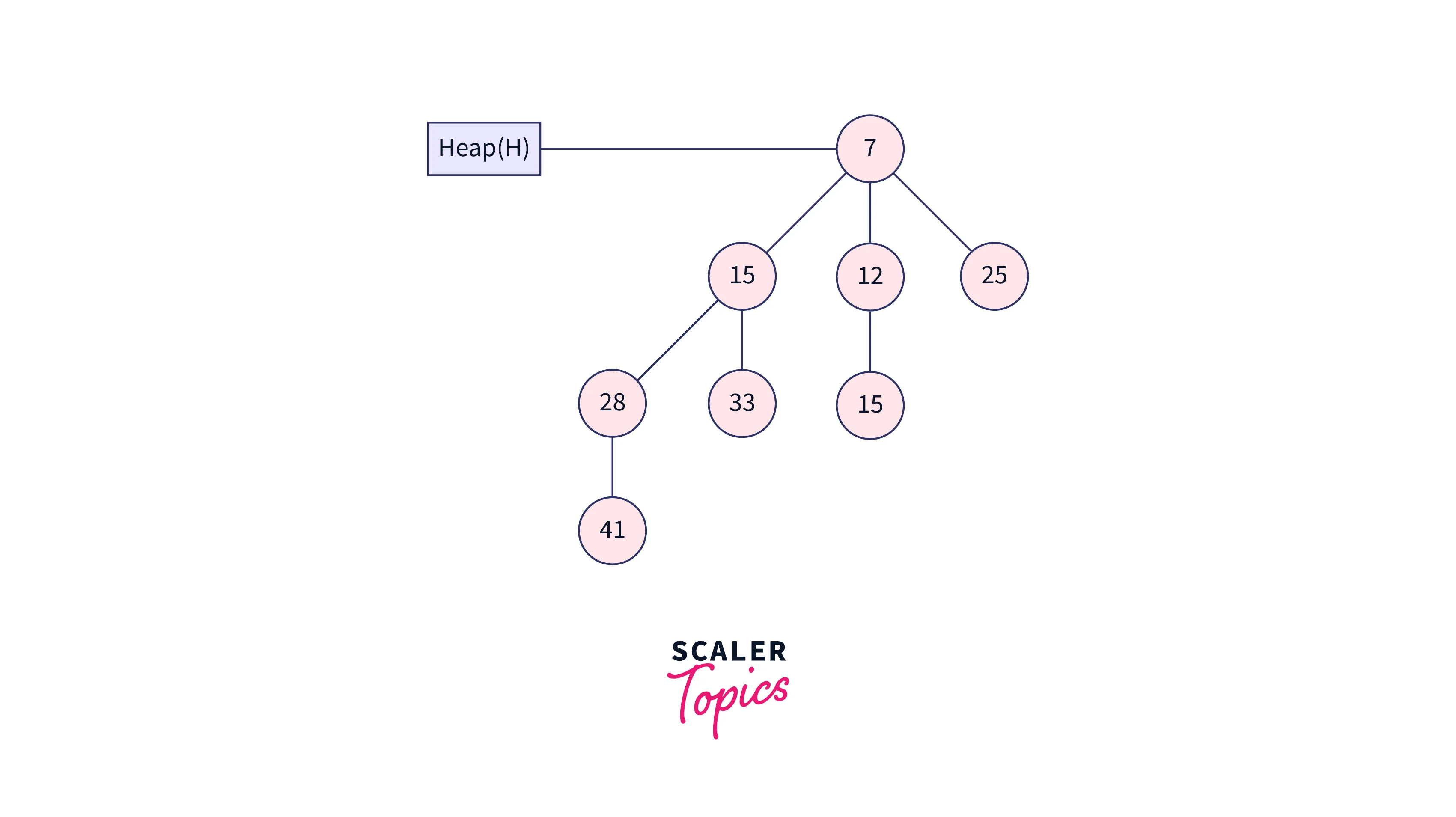
This implies that we must eliminate an element with the smallest key value. As is common knowledge, the root element of a min-heap contains the smallest key value. Therefore, we must compare the root node’s key value across all binomial trees. Let’s look at an illustration of how to extract the smallest key from a heap.
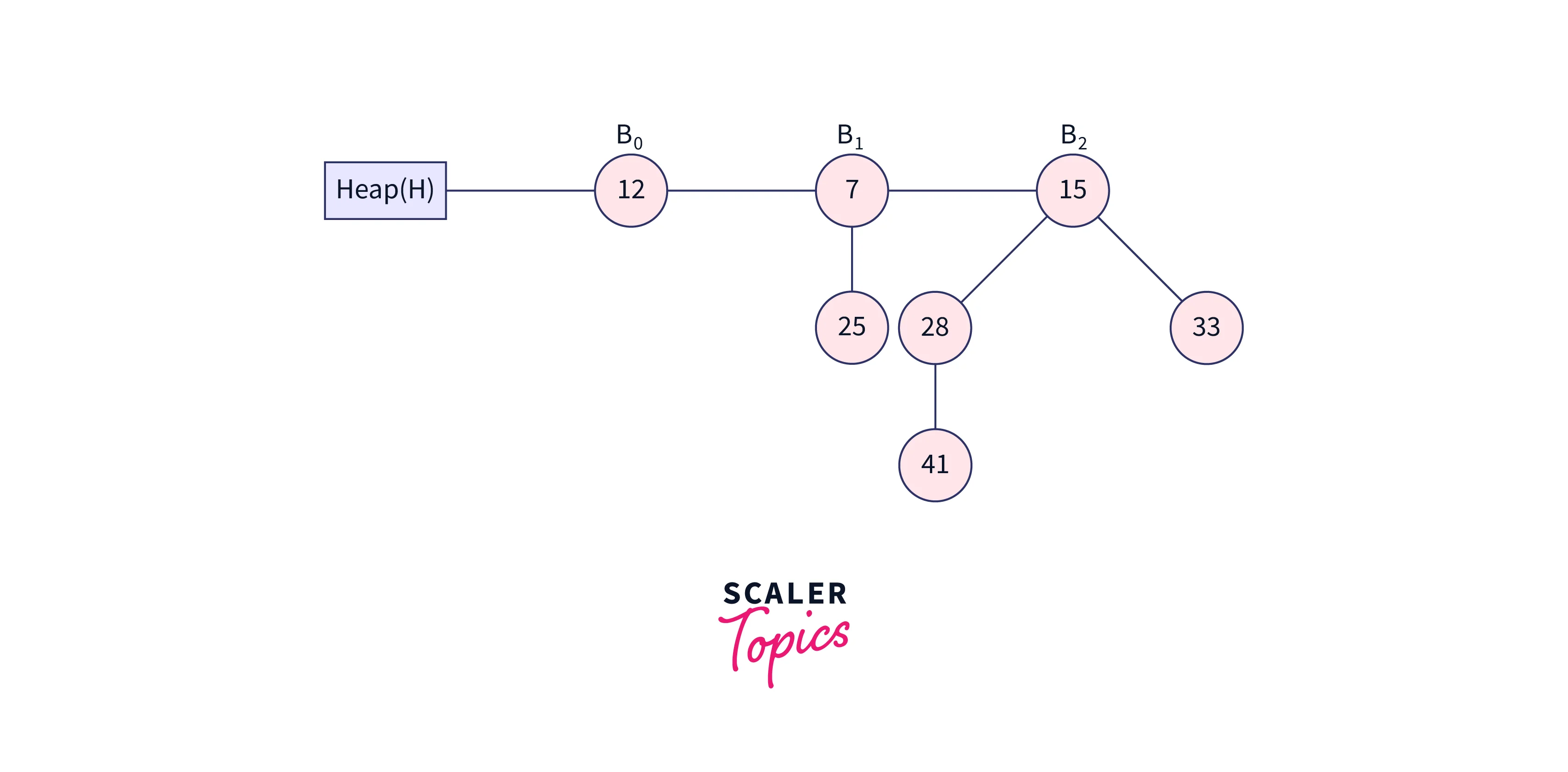
Compare the root node key values of the binomial trees in the heap above now. In the above heap, where 7 is the minimum value, 12, 7, and 15 are the root node’s key values. As a result, remove node 7 from the tree as shown in the image below.
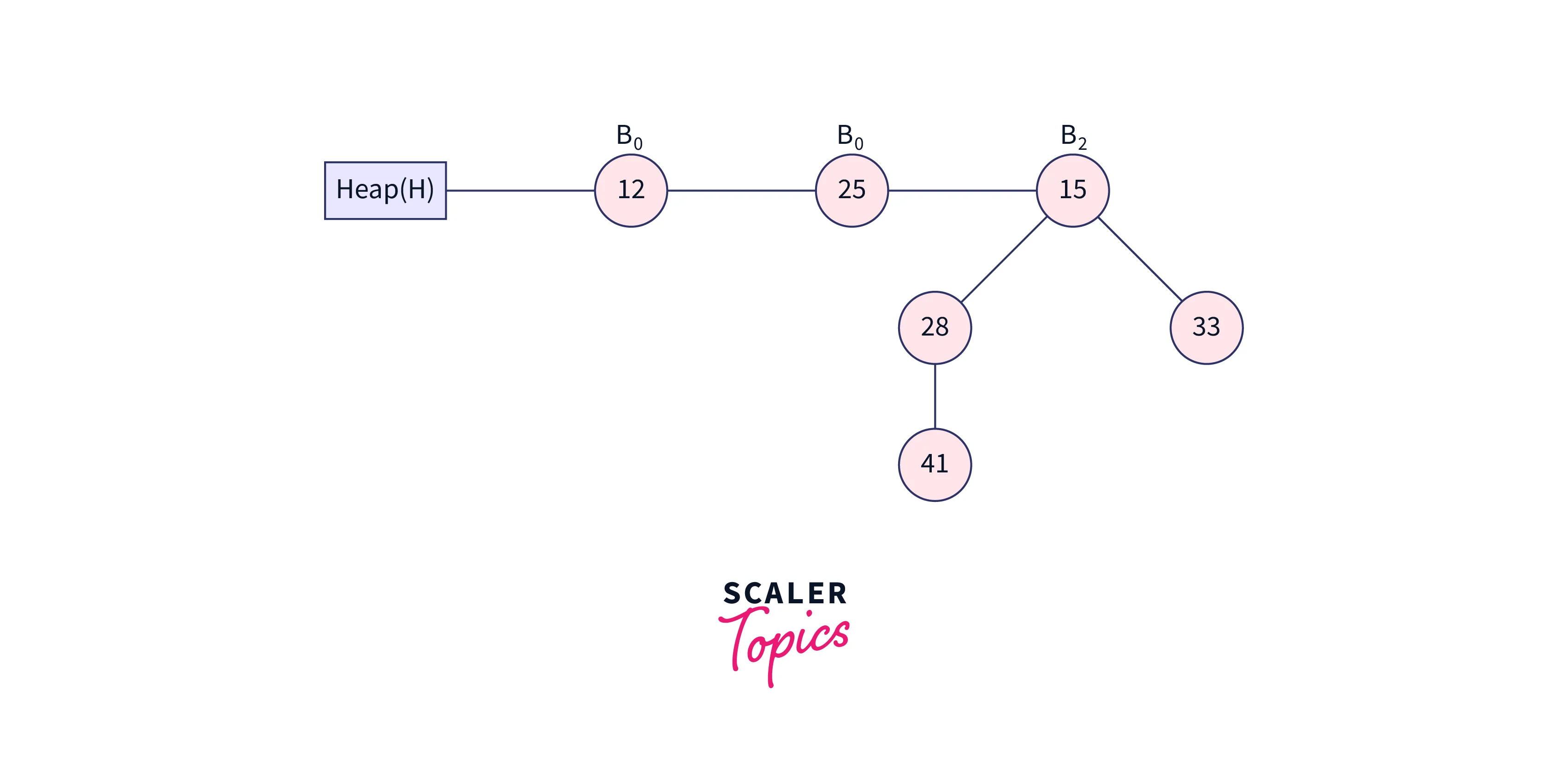
Nodes 12 and 25 now have degrees of B0, while node 15 has a degree of B2. Node 12 is indicated by pointer x, node 25 by next(x), and node 15 by sibling(next(x)). Because the degree of x is equal to the degree of next(x), but not to the degree of sibling(next(x)). As shown in the below image, node 25 will be removed and attached to node 12 because the value of pointer x is less than the value of pointer next(x).
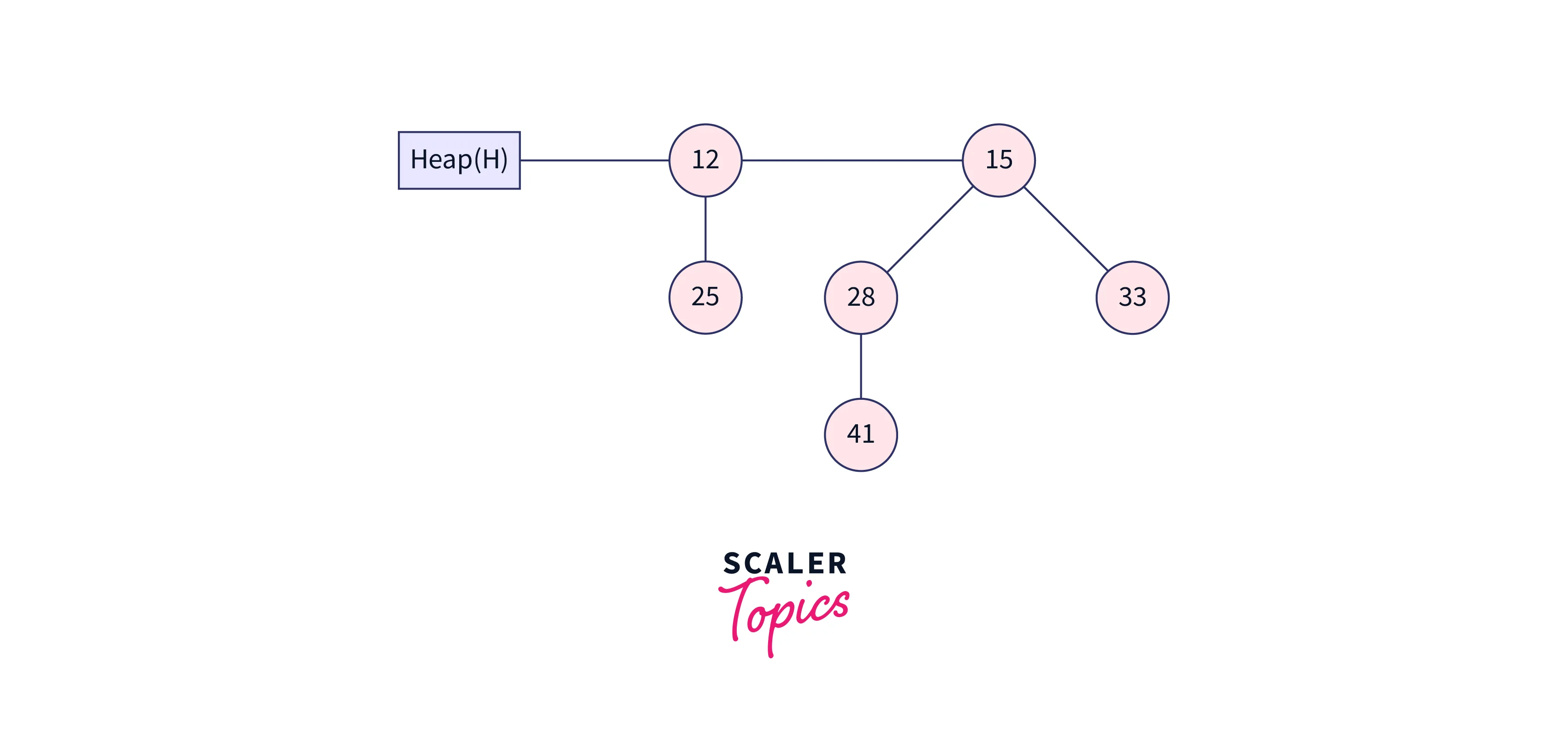
Node 12’s degree has now been changed to B1. After extracting the minimum key, the heap shown above is the result.
Decreasing a Key
Let’s proceed to the subsequent operation on the binomial heap. Once the key’s value is reduced, it may become smaller than the key of its parent, which constitutes a violation of the min-heap property. After lowering the key, if such a situation arises, swap the element with its parent, grandparent, and so forth until the min-heap property is met.
Let’s use an example to comprehend how to decrease a key in a binomial heap. Take a look at the heap below:
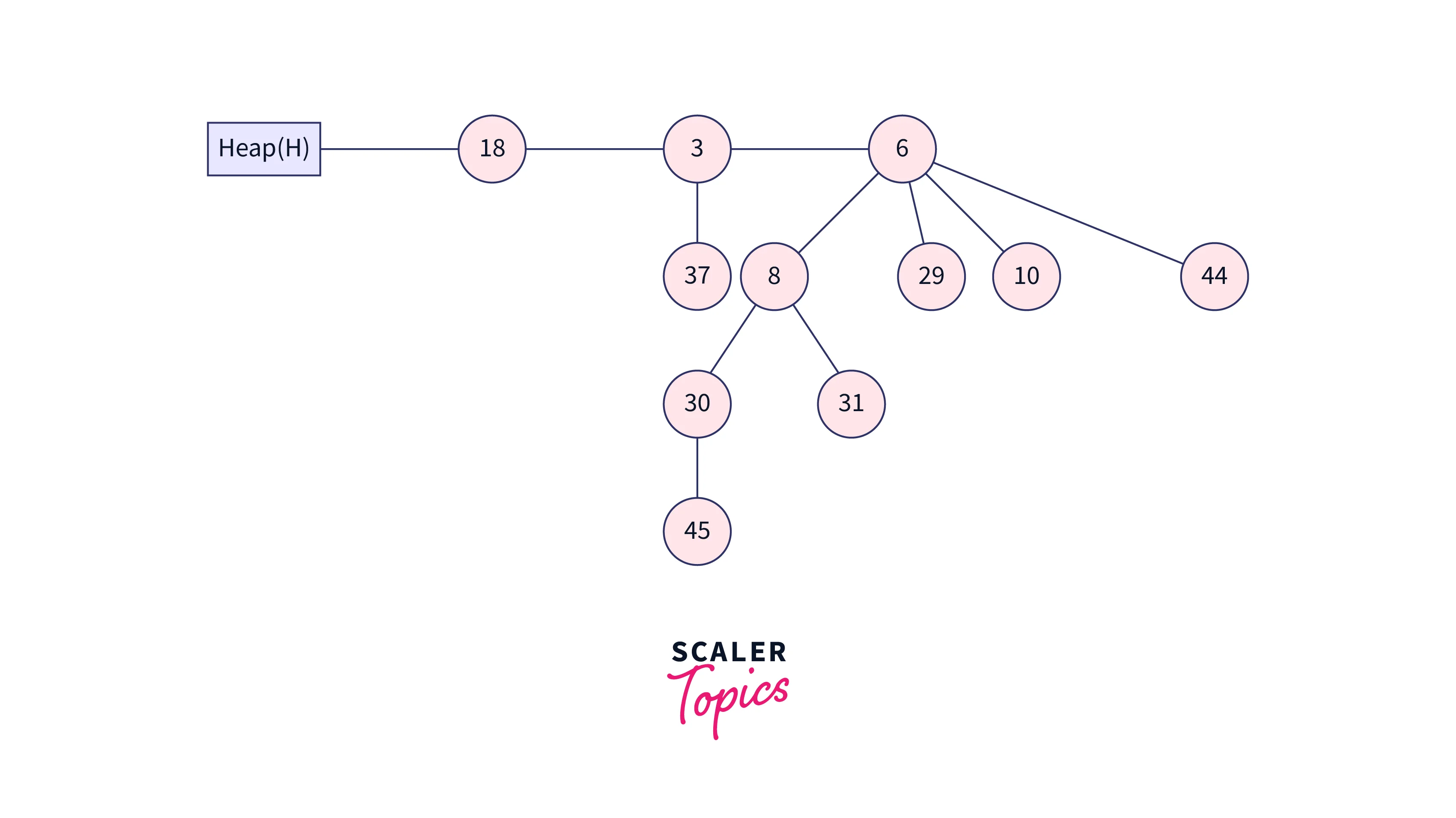
Decrease the key 45 by 7 from the above heap. The heap will be after 45 has been decreased by 7.
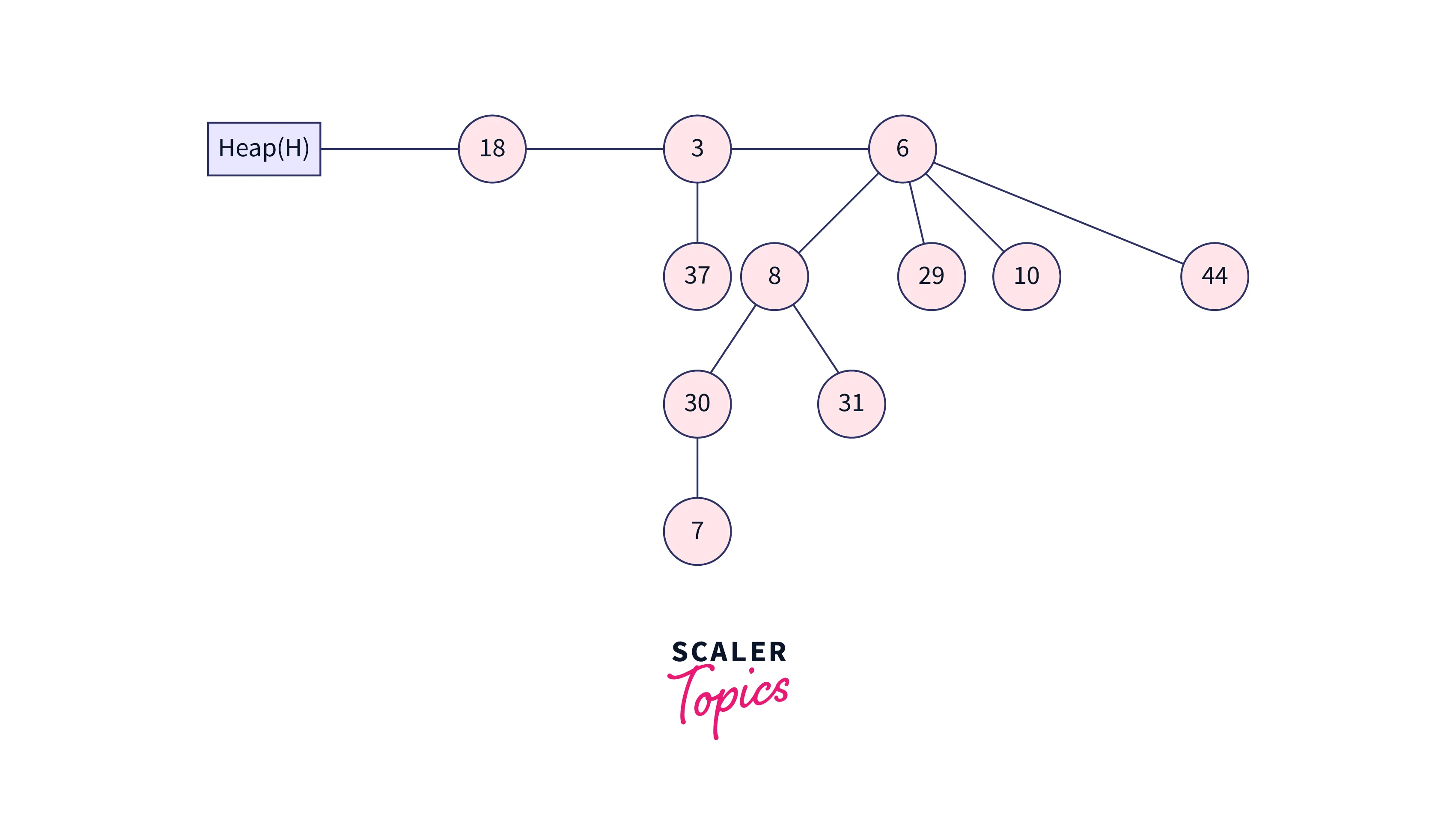
The above heap’s min-heap property is broken after the key is decreased. Now compare 7 to its parent number 30, and since 7 is less than 30, you can swap 7 for 30 to get the following heap:
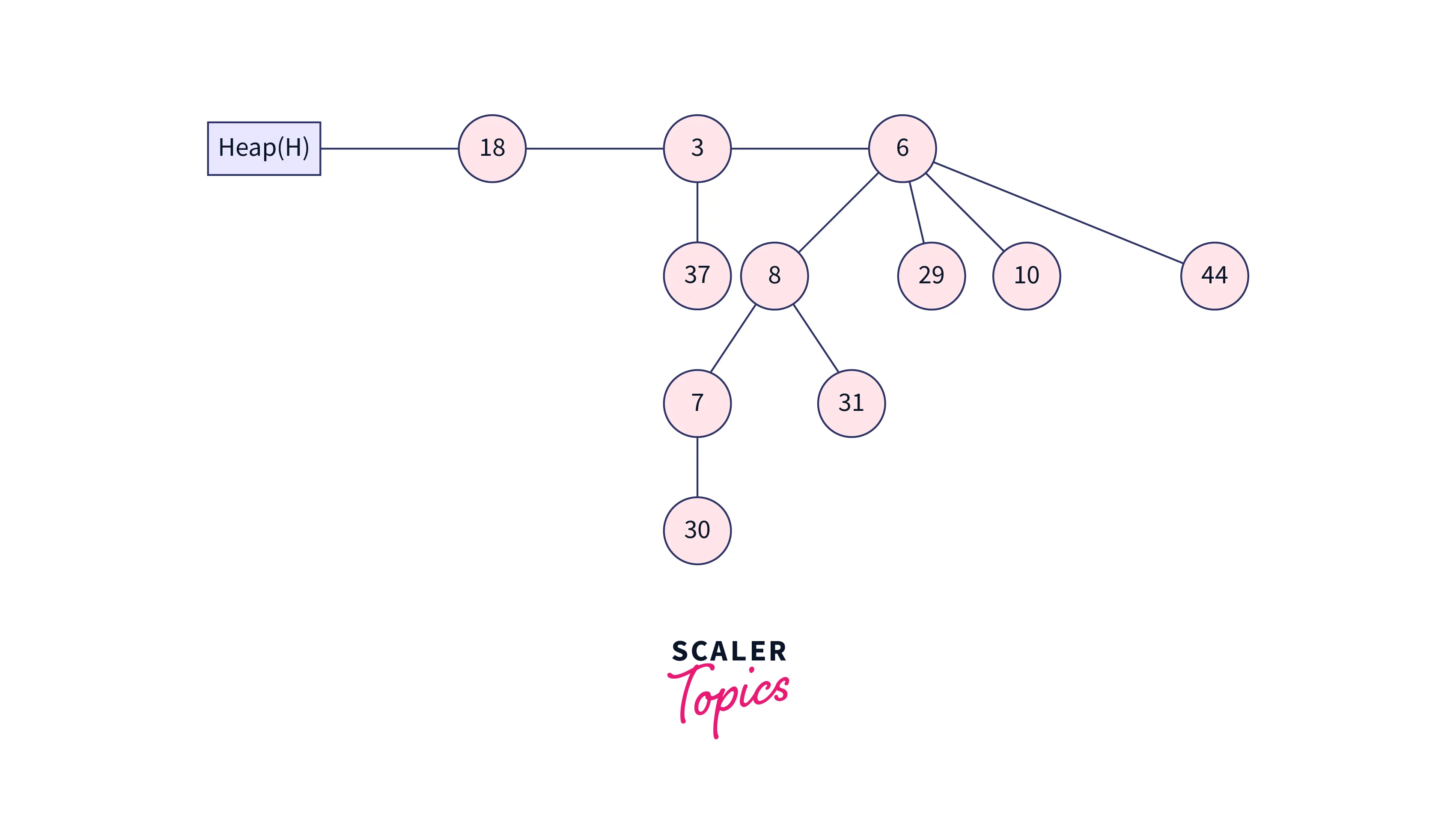
The element 7 will be less than its parent element 8 when compared to it once more, so the two elements will be switched, and the resultant heap will be.
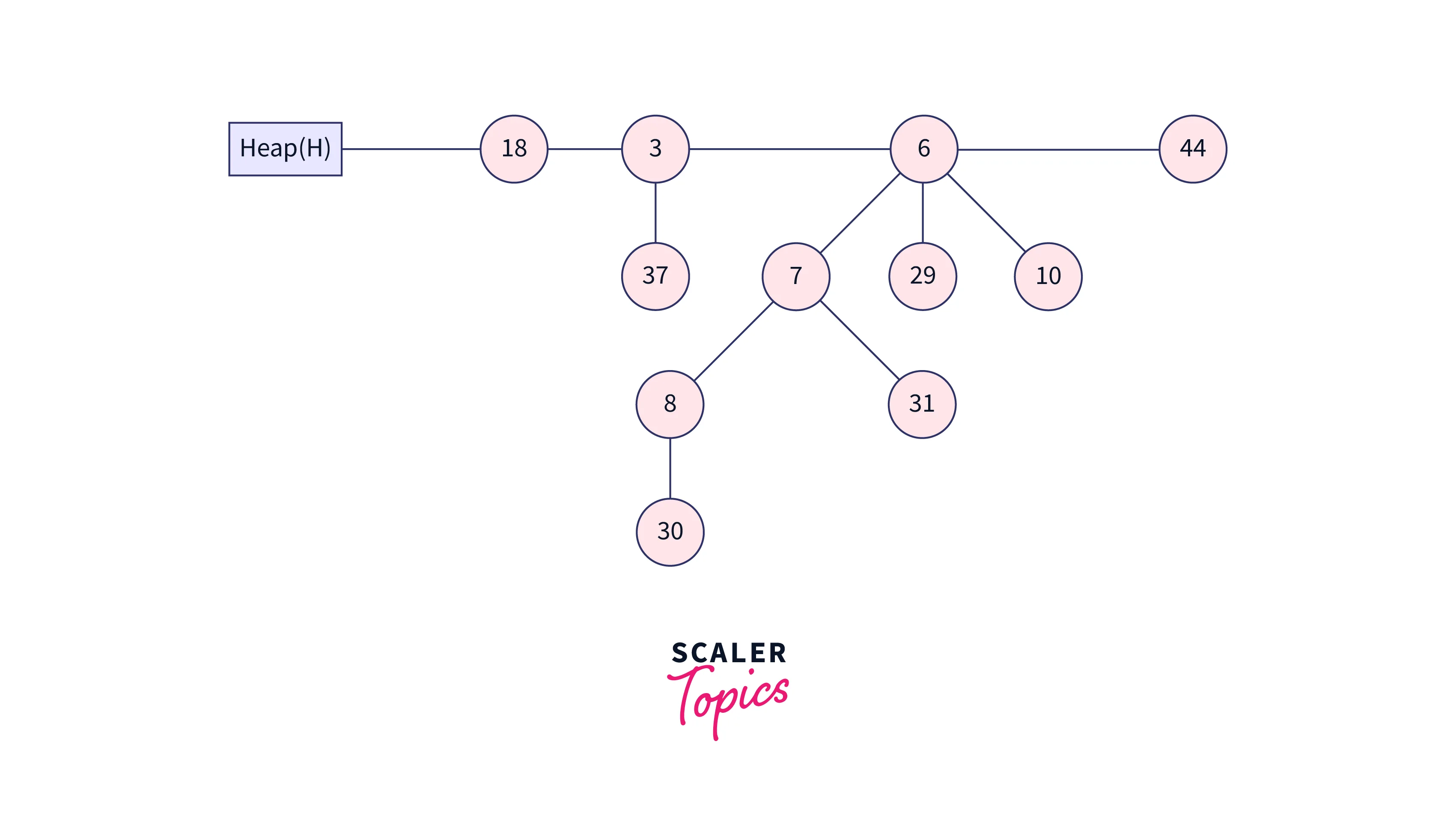
The above heap now satisfies the min-heap property. The last heap after decreasing a key is therefore the one mentioned above.
Delete a Node
The minimum node in the heap must be deleted to remove a node from the heap. To do this, we must first reduce the key of the node to negative infinity (or -). With the aid of an example, we’ll now see how to delete a node. Let’s say we need to remove node 41 from the heap in the example below.
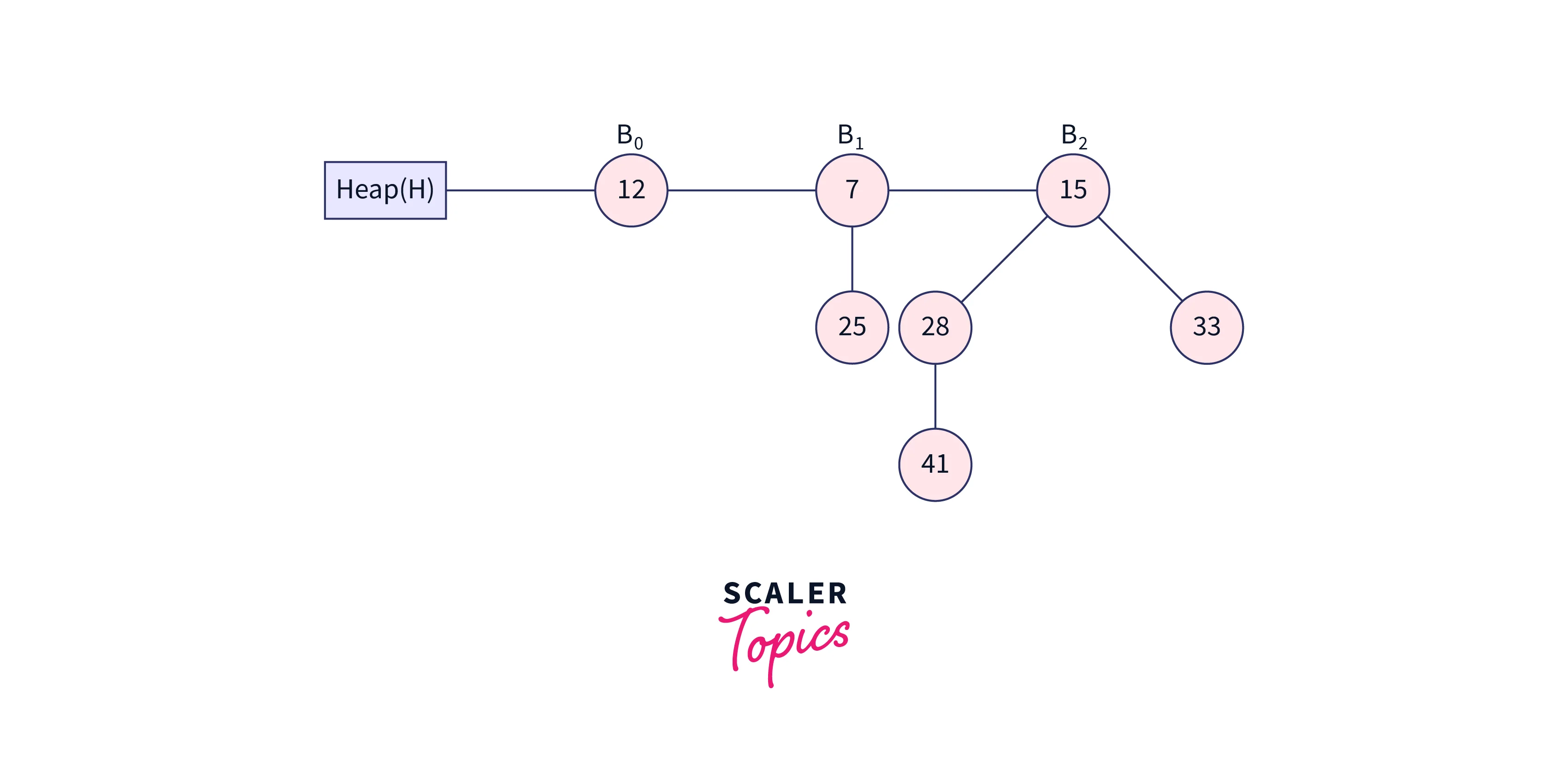
First, replace the node with negative infinity (or -∞) as shown below:
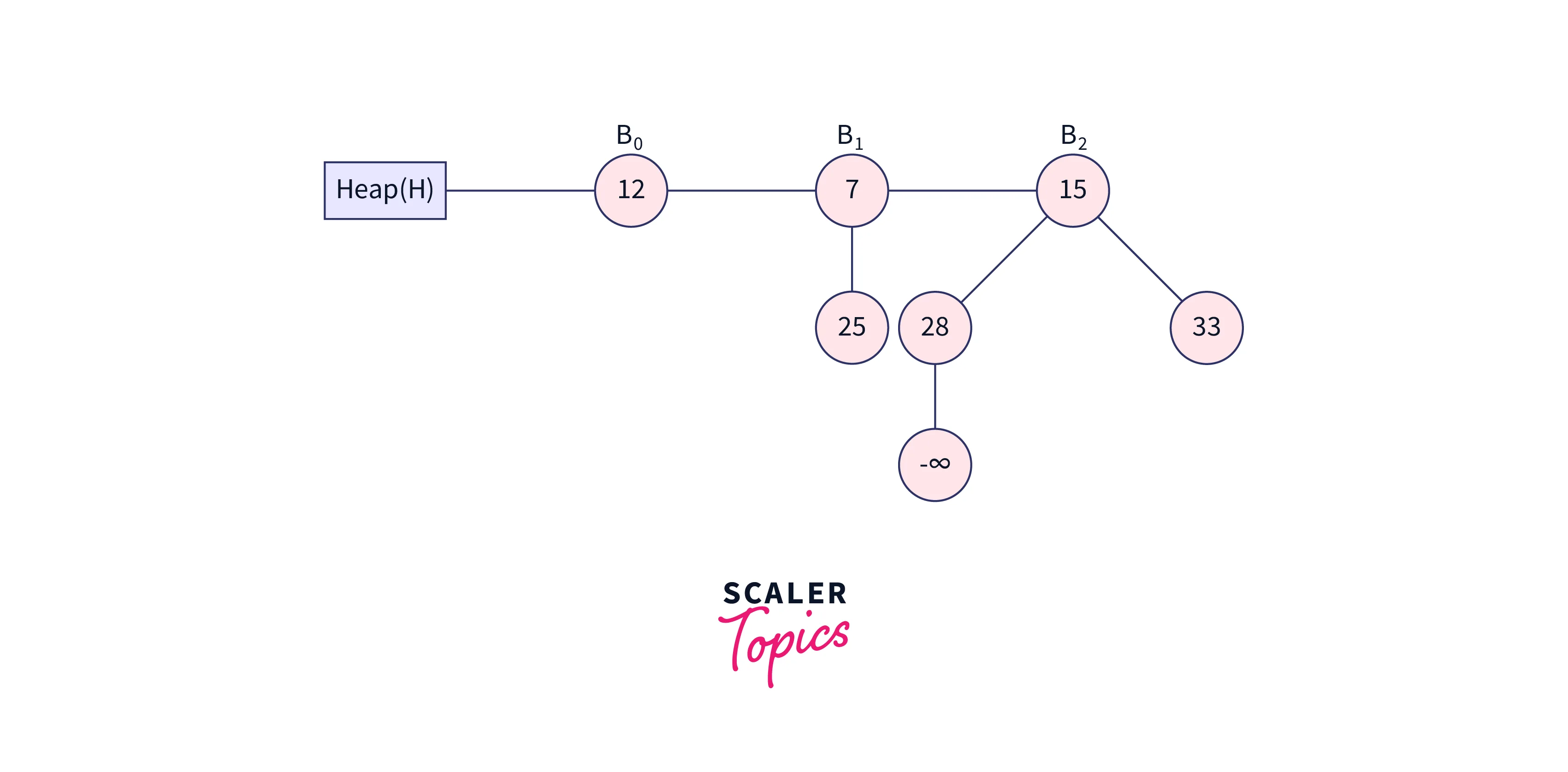
To maintain the min-heap property, swap the negative infinity with its root node.
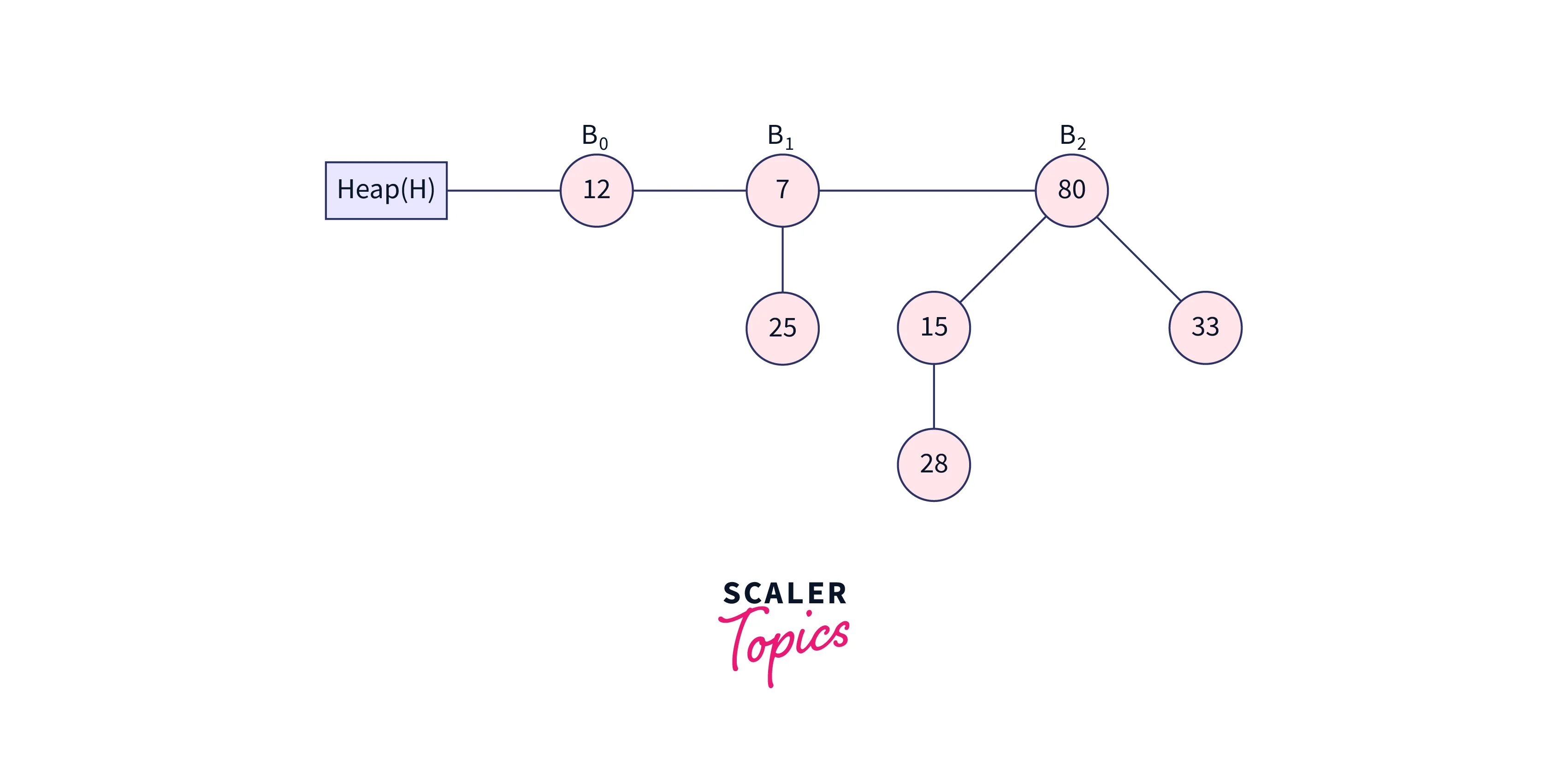
Extraction of the smallest key from the heap is the following step. We will extract this key because the minimum key in the aforementioned heap is -infinity, and the heap would be:
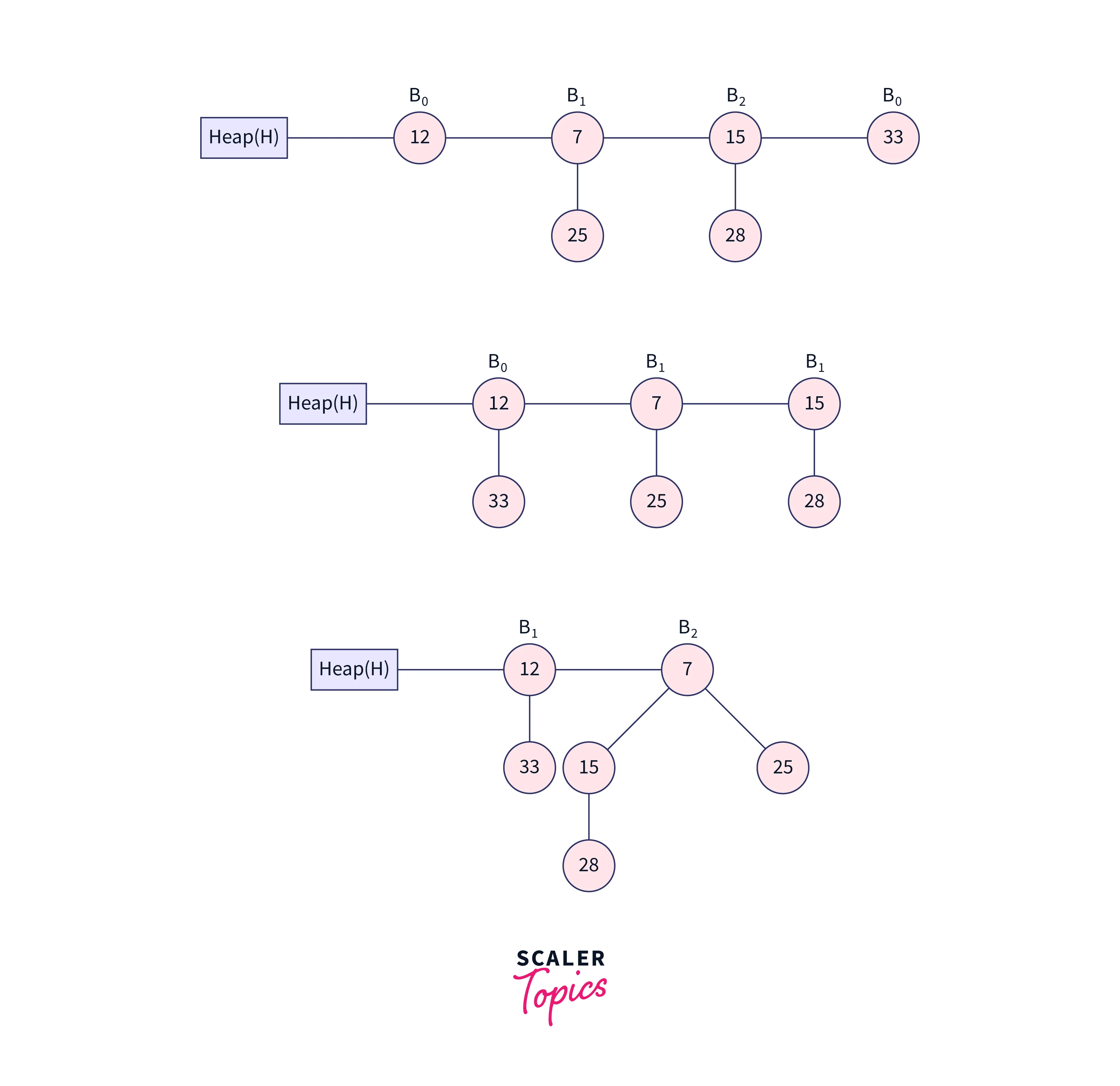
The above is the final heap after deleting node 41.
Complexity of Binomial Heap
| Operations | Time Complexity |
|---|---|
| Making a Heap | O(logn) |
| Inserting a node | O(logn) |
| Extracting Minimum key | O(logn) |
| Union or merging | O(logn) |
| Decreasing a Key | O(logn) |
| Deleting a node | O(logn) |
| Finding the Minimum key | O(logn) |
Represent Binomial Heap
- A binomial heap is a collection of binomial trees.
- The binomial tree should be arranged or represented in such a way that it allows sequential access to all of its siblings from the leftmost sibling.
- The key concept is to represent binomial trees with each node storing two pointers, one to the leftmost child and the other to the right sibling.
Conclusion
- The heap is a tree-based structure that is a complete binary tree. The binomial tree is of orders
0and1. - There should be at least one binomial tree in the binomial heap. It is mainly used to implement the priority queue.
- The Binomial tree Bk is the ordered tree made of linking two binomial trees, Bk-1 in which one becomes the leftmost child or the other.
- The binomial heap can be used to represent the binary number also, i.e., if the binomial heap has n binomial trees, where n is the number of set bits in the binary representation of the number.
- The idea is to represent Binomial Trees as the leftmost child and right-sibling representation, which means that each node stores two pointers, one to the leftmost child and one to the right sibling.
- The minimum node in the heap must be deleted to remove a node from the heap.
- The root element of a min-heap contains the smallest key value. Therefore, we must compare the root node’s key value across all binomial trees.
