Binary Search Tree (BST)

A binary search tree (BST) is a sorted binary tree, where we can easily search for any key using the binary search algorithm. To sort the BST, it has to have the following properties: The node’s left subtree contains only a key that’s smaller than the node’s key.

Takeaways

• Complexity of binary search tree algorithm
  • Time complexity –
    • Insertion : O(n)
    • Searching (h) (h: Height of the binary search tree)
    • Deletion : O(n)

Searching is a trivial part of everyday life. It’s found in almost every aspect of our lives. If you would like to read more about searching and its applications, you can have a quick read about the Linear Search Algorithm.

Today we’ll learn about an important searching algorithm, which is much more scalable and robust than it’s near sibling and inspiration, Binary Search called Binary Search Trees or BSTs.

Introduction to Binary Search Tree

Binary Search Trees, as you can see, is composed of two main programming aspects; Binary Search and Trees.

Binary Search is one of the fastest and optimized searching algorithms out there. If you haven’t got a chance to read about it, I would highly recommend going through the Binary Search article. It will help you understand Binary Search Trees super easily.

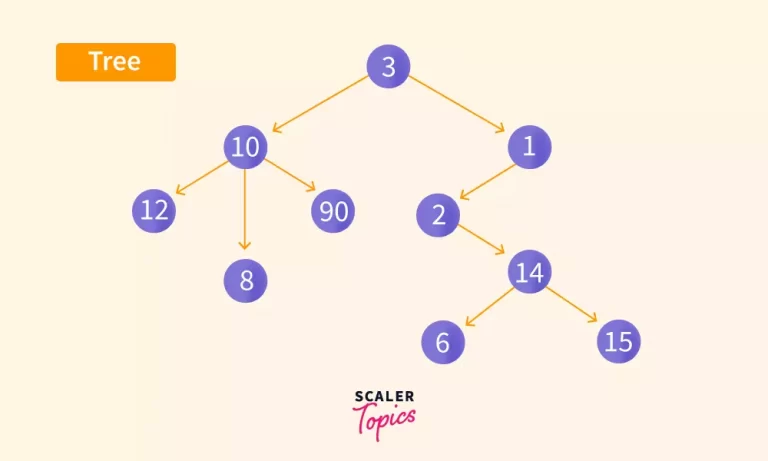
Trees on the other hand, is a widely used data structure which represents an actual hierarchical tree structure.

A tree consists of a root node (the topmost node of the tree) and each node can have some number of children nodes.

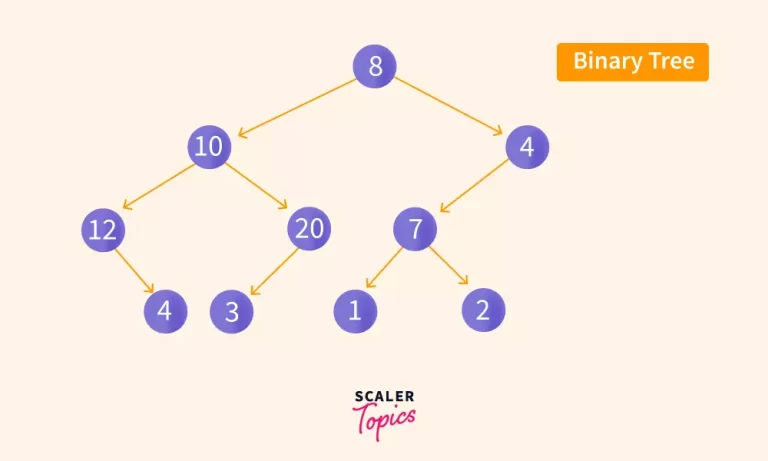
Binary Trees are the most commonly used version of trees wherein each node of the tree can have utmost two child nodes. To simplify, each node, including the root node will either have 0, 1 or 2 children, not more or less than that.

A node which has 0 children is called a leaf node. In the above figure; 4, 3, 1, 2 are the leaf nodes as they have no child nodes.

Now that we know a little about Binary Search, Trees and Binary Trees, let’s see how a Binary Search Tree works and looks like.

Why do we Need Binary Search Trees?

Let’s say you have a stream of integers where integers are constantly getting added in the end and at any point of time, you want to check whether a particular integer was present in the stream till now or not.

stream: 5 8 1 12 3 18 37 15

Let’s say you want to check whether an integer, K = 11 was present in this stream or not.

If you try to apply Binary Search here, firstly you’ll have to sort the integers you have till now. Then, you can apply binary search to check whether K = 11 is present in the sorted array or not, which as of now is not.

sorted: 1 3 5 8 12 15 18 37

What’s the time complexity till now?

Binary Search Trees (BSTs) are beneficial for dynamic datasets as they provide efficient search, insert, and delete operations with an average time complexity of O(log₂N). Unlike sorted arrays, BSTs can handle stream updates effectively without requiring a complete resorting of the dataset.

What is a Binary Search Tree?

Binary Search Trees are special kinds of Binary Trees which have a few special properties. The idea is similar to the classical Binary Search algorithm. The only subtle difference is that it uses Binary Trees to represent the data set. Let’s see how.

Let’s talk about the special properties of a Binary Search Tree.

1. The value of all the nodes in the left subtree of the root node is less than the value of the root node.
2. The value of all the nodes in the right subtree of the root node is greater than the value of the root node.
3. Properties 1 and 2 are true for all the nodes of the tree.

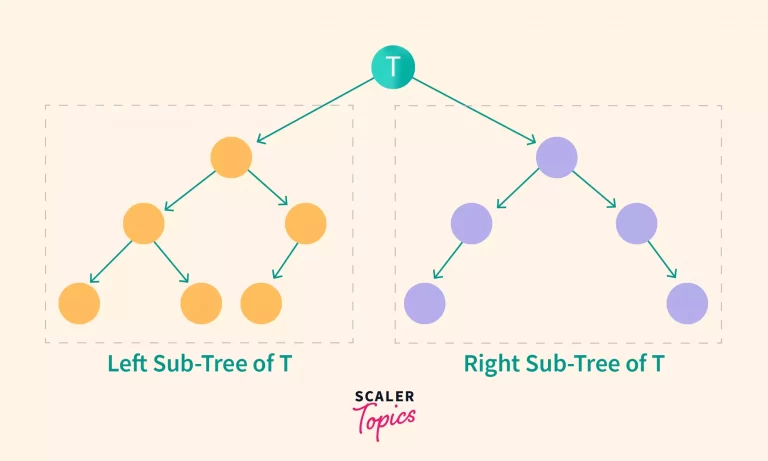
A subtree of a tree rooted at T is a tree which contains all the descendants (children, grandchildren, and so on) of the node T.

Any Binary Tree which follows the above properties is said to be a Binary Search Tree.

But wait wait wait!!! What about duplicate values? Here, we have a couple of options.

1. If we want to store only unique values in our Binary Search Tree, we can do nothing and just ignore if a duplicate value is being inserted.
2. If we want to store duplicate duplicate values in our Binary Search Tree, we can insert in either the left or the right subtree. But not both. We have to choose one beforehand and stick with it.

For our examples, we have chosen to always insert duplicate values in the left subtree of a node.

Therefore, all elements less than or equal to the current node will be present in the left subtree and all elements which are strictly greater than the current node will be present in the right subtree.

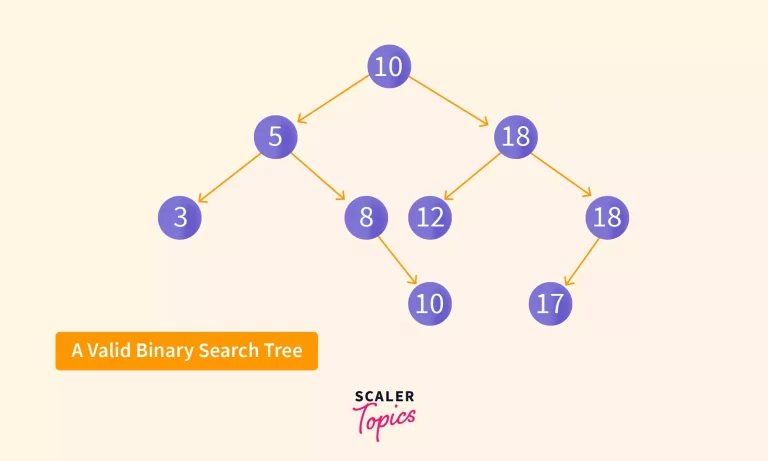
In the above binary tree, all the values in the left subtree of 10 are less than or equal to 10. Similarly, for all the other nodes in the tree, the values in the left subtree are less than the root node.

On the other hand, in the above tree, the value 9 in the left subtree of 7 is greater than the root node, 7. Hence, this node violates the first property and thus, it is not a Binary Search Tree.

Operations on a Binary Search Tree

Now that we know the properties of a Binary Search Tree, let’s look at some of the basic operations that can be performed on it. P.S. All the code snippets are in Java 8.

Each node of a Binary Search Tree can be represented as follows.

class Node {
    int key;
    Node left;
    Node right;
}

The Node class in a Binary Search Tree contains left and right child nodes, along with a key field representing the node’s value. Nodes are compared based on the key field, enabling us to use these properties for element insertion and search in the Binary Search Tree.

Insert

Let’s say the element we’re trying to insert is K. Below is the algorithm for insert operation in a Binary Search Tree.

1. if node == null, create a new node with the value of the key field equal to K. We return this newly created node directly from here.
2. if K <= node.key, it means K must be inserted in the left subtree of the current node. We repeat(recur) the process from step 1 for the left subtree.
3. else K > node.key, which means K must be inserted in the right subtree of the current node. We repeat(recur) the process from step 1 for the right subtree.
4. Return the current node.

Let’s say we are trying to insert the following integers in the Binary Search Tree.

10 15 5 8 18 12 10

The below gif demonstrates how the above elements are inserted one by one.

Search

In the Binary Search Tree, the search algorithm for element K is as follows:

• If the node is null, K is not present in the tree, so we return null.
• If K is less than the node’s key, we repeat the process from step 1 for the left subtree.
• If K is greater than the node’s key, we repeat the process from step 1 for the right subtree.
• If K is equal to the node’s key, we have found K in the tree and return the current node.

The search algorithm closely resembles the insert algorithm, but instead of creating a new node, we directly return the node when we find the element. If the node is null, it signifies that K is not present in the Binary Search Tree, and we return null to indicate this.

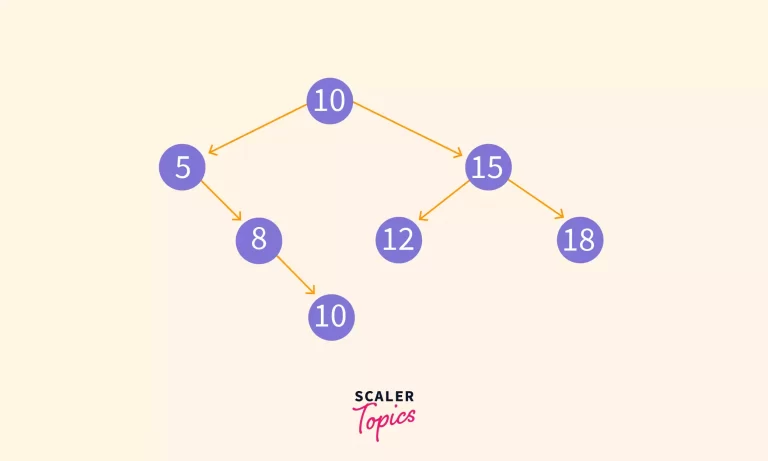
Let’s say we’re trying to search K = 12 in the above tree. The below gif shows how the nodes are compared in each step.

In the end, we were able to find 12 successfully.

Let’s try to find an element which is not present in the BST, say K = 9. The below gif shows how the nodes are compared in each step and in the end, we reach a null node, which means 9 is not present in the BST.

Pre-Order Traversal

The traversals of a Binary Search Tree are similar to that of any Binary Tree.

Below is the algorithm for the pre-order traversal of a Binary Search Tree.

1. if node == null, do nothing. else, do steps 2, 3, 4.
2. print the current node.
3. Visit the left subtree and repeat step 1.
4. Visit the right subtree and repeat step 1.

If the node is null, we don’t do anything.

If it is non-null, we first visit the current node, then the left subtree and then the right subtree.

In-Order Traversal

Below is the algorithm for the in-order traversal of a Binary Search Tree.

1. if node == null, do nothing. else, do steps 2, 3, 4.
2. Visit the left subtree and repeat step 1.
3. print the current node.
4. Visit the right subtree and repeat step 1.

If the node is null, we don’t do anything.

If it is non-null, we first visit the left subtree, then the current node and then the right subtree.

Post-Order Traversal

Below is the algorithm for the post-order traversal of a Binary Search Tree.

1. if node == null, do nothing. else, do steps 2, 3, 4.
2. Visit the left subtree and repeat step 1.
3. Visit the right subtree and repeat step 1.
4. print the current node. If the node is null, we don’t do anything.

If it is non-null, we first visit the left subtree, then the right subtree and then the current node.

Implementation of Binary Search Trees

Binary Search Tree in Java

class Node {
    int key;
    Node left;
    Node right;

    public Node(int key) {
        this.key = key;
    }
}

class `BST` {
    private Node root;

    public void insert(int key) {
        root = insert(root, key);
    }

    private Node insert(Node node, int key) {
        if (node == null) {
            return new Node(key);
        }
        if (key <= node.key) {
            node.left = insert(node.left, key);
        } else {
            node.right = insert(node.right, key);
        }
        return node;
    }

    public Node search(int key) {
        return search(root, key);
    }

    private Node search(Node node, int key) {
        if (node == null || node.key == key) {
            return node;
        }
        if (key <= node.key) {
            return search(node.left, key);
        }
        return search(node.right, key);
    }

    public void inOrder() {
        System.out.print("The inOrder traversal is: ");
        inOrder(root);
        System.out.println();
    }

    private void inOrder(Node node) {
        if (node == null) {
            return;
        }
        inOrder(node.left);
        System.out.print(node.key + " ");
        inOrder(node.right);
    }

    public void preOrder() {
        System.out.print("The preOrder traversal is: ");
        preOrder(root);
        System.out.println();
    }

    private void preOrder(Node node) {
        if (node == null) {
            return;
        }
        System.out.print(node.key + " ");
        preOrder(node.left);
        preOrder(node.right);
    }

    public void postOrder() {
        System.out.print("The postOrder traversal is: ");
        postOrder(root);
        System.out.println();
    }

    private void postOrder(Node node) {
        if (node == null) {
            return;
        }
        postOrder(node.left);
        postOrder(node.right);
        System.out.print(node.key + " ");
    }
}

public class BinarySearchTree {
    public static void main(String[] args) {
        `BST` `bst` = new `BST`();
        `bst`.insert(10);
        `bst`.insert(15);
        `bst`.insert(5);
        `bst`.insert(8);
        `bst`.insert(18);
        `bst`.insert(12);
        `bst`.insert(10);

        `bst`.preOrder();
        `bst`.inOrder();
        `bst`.postOrder();

        search(`bst`, 12);
        search(`bst`, 9);
    }

    private static void search(`BST` `bst`, int key) {
        if (`bst`.search(key) != null) {
            System.out.println(key + " found");
        } else {
            System.out.println(key + " not found");
        }
    }
}

Output:

The preOrder traversal is: 10 5 8 10 15 12 18 
The inOrder traversal is: 5 8 10 10 12 15 18 
The postOrder traversal is: 10 8 5 12 18 15 10 
12 found
9 not found

Binary Search Tree in C++

#include <iostream>
using namespace std;

class Node
{
public:
    int key;
    Node *left;
    Node *right;

    Node(int key)
    {
        this->key = key;
        this->left = this->right = NULL;
    }
};

class `BST`
{
private:
    Node *root;

    Node *insert(Node *node, int key)
    {
        if (node == NULL)
        {
            return new Node(key);
        }
        if (key <= node->key)
        {
            node->left = insert(node->left, key);
        }
        else
        {
            node->right = insert(node->right, key);
        }
        return node;
    }

    Node *search(Node *node, int key)
    {
        if (node == NULL || node->key == key)
        {
            return node;
        }
        if (key < node->key)
        {
            return search(node->left, key);
        }
        return search(node->right, key);
    }

    void inOrder(Node *node)
    {
        if (node == NULL)
        {
            return;
        }
        inOrder(node->left);
        cout << node->key << " ";
        inOrder(node->right);
    }

    void preOrder(Node *node)
    {
        if (node == NULL)
        {
            return;
        }
        cout << node->key << " ";
        preOrder(node->left);
        preOrder(node->right);
    }

    void postOrder(Node *node)
    {
        if (node == NULL)
        {
            return;
        }
        postOrder(node->left);
        postOrder(node->right);
        cout << node->key << " ";
    }

public:
    `BST`()
    {
        this->root = NULL;
    }

    void insert(int key)
    {
        root = insert(root, key);
    }

    Node *search(int key)
    {
        return search(root, key);
    }

    void inOrder()
    {
        cout << "The inOrder traversal is: ";
        inOrder(root);
        cout << "\n";
    }

    void preOrder()
    {
        cout << "The preOrder traversal is: ";
        preOrder(root);
        cout << "\n";
    }

    void postOrder()
    {
        cout << "The postOrder traversal is: ";
        postOrder(root);
        cout << "\n";
    }
};

static void search(`BST` `bst`, int key)
{
    if (`bst`.search(key) != NULL)
    {
        cout << key << " found\n";
    }
    else
    {
        cout << key << " not found\n";
    }
}

int main()
{
    `BST` `bst`;
    `bst`.insert(10);
    `bst`.insert(15);
    `bst`.insert(5);
    `bst`.insert(8);
    `bst`.insert(18);
    `bst`.insert(12);
    `bst`.insert(10);

    `bst`.preOrder();
    `bst`.inOrder();
    `bst`.postOrder();

    search(`bst`, 12);
    search(`bst`, 9);
}

Output:

The preOrder traversal is: 10 5 8 10 15 12 18 
The inOrder traversal is: 5 8 10 10 12 15 18 
The postOrder traversal is: 10 8 5 12 18 15 10 
12 found
9 not found

Binary Search Tree in Python

class Node:
    def __init__(self, key):
        self.key = key
        self.left = None
        self.right = None


class `BST`:
    def __init__(self):
        self.root = None

    def insert(self, key):
        self.root = self.__insert__(self.root, key)

    def __insert__(self, node, key):
        if node is None:
            return Node(key)

        if key <= node.key:
            node.left = self.__insert__(node.left, key)

        else:
            node.right = self.__insert__(node.right, key)

        return node

    def search(self, key):
        return self.__search__(self.root, key)

    def __search__(self, node, key):
        if node is None or node.key == key:
            return node

        if key <= node.key:
            return self.__search__(node.left, key)

        return self.__search__(node.right, key)

    def inOrder(self):
        print("The inOrder traversal is: ", end=" ")
        self.__inOrder__(self.root)
        print()

    def __inOrder__(self, node):
        if node == None:
            return

        self.__inOrder__(node.left)
        print(node.key, end=" ")
        self.__inOrder__(node.right)

    def preOrder(self):
        print("The preOrder traversal is: ", end=" ")
        self.__preOrder__(self.root)
        print()

    def __preOrder__(self, node):
        if node == None:
            return

        print(node.key, end=" ")
        self.__preOrder__(node.left)
        self.__preOrder__(node.right)

    def postOrder(self):
        print("The preOrder traversal is: ", end=" ")
        self.__postOrder__(self.root)
        print()

    def __postOrder__(self, node):
        if node == None:
            return

        self.__postOrder__(node.left)
        self.__postOrder__(node.right)
        print(node.key, end=" ")


def search(`bst`, key):
    if `bst`.search(key) != None:
        print(key, "found")
    else:
        print(key, "not found")


`bst` = `BST`()
`bst`.insert(10)
`bst`.insert(15)
`bst`.insert(5)
`bst`.insert(8)
`bst`.insert(18)
`bst`.insert(12)
`bst`.insert(10)

`bst`.preOrder()
`bst`.inOrder()
`bst`.postOrder()

search(`bst`, 12)
search(`bst`, 9)

Output:

The preOrder traversal is:  10 5 8 10 15 12 18 
The inOrder traversal is:  5 8 10 10 12 15 18 
The preOrder traversal is:  10 8 5 12 18 15 10 
12 found
9 not found

Complexity of Binary Search Trees

Since the insert and search operation are pretty similar, we can say the time and space complexity will be similar for both of them.

Also, all the traversals are pretty similar as well. So we can say the time and space complexity are the same for all of them.

Time Complexity of Binary Search Tree

Insert/Search

The time complexity of Binary Search Tree operations depends on the height of the tree. If the tree becomes heavily skewed due to elements being inserted in a sorted increasing order, the worst-case time complexity for insert/search operations is O(N). However, if elements are inserted randomly, creating a balanced tree, the average time complexity for each operation is O(log₂N), where N is the number of elements in the tree.

Traversals

For the traversals, we have to visit all the nodes of the tree. It doesn’t matter the order in which we visit them. We end up visiting all of them.

Hence, the time complexity will always be O(N).

Space Complexity of Binary Search Tree

Insert/Search

The space complexity of Binary Search Tree operations is O(1) as the memory requirement is constant. The space complexity depends on the implementation used, but ignoring the recursion stack, it remains constant for both insert and search operations. The total space complexity for N insertions is O(N).

Traversals

This space complexity of all the traversals can be thought of in a similar way.

Since we don’t use any extra memory other than the recursion stack, the space complexity is constant, i.e. O(1) for all the traversals.

Food for thought: In the examples above, our data set consisted of integers only. If our data set consists of strings only, what do you think the time and space complexity will be in that case? 😛

Applications of Binary Search Trees

Binary Search Trees are suitable for dynamic and constantly updated datasets, with efficient insertions and deletions. However, the drawback arises when elements are inserted in an order that imbalances the tree, leading to increased costs for operations.

To address this, balanced Binary Search Tree implementations automatically balance themselves, ensuring a height of O(log₂N), regardless of the insertion order.

Moreover, Binary Search Trees can be utilized to sort dynamic datasets. The in-order traversal of the tree provides the elements in sorted increasing order, making it convenient to obtain the sorted order of the elements in real-time.

In summary, Binary Search Trees are advantageous for dynamic datasets, offer self-balancing capabilities, and can be utilized for efficient sorting through in-order traversal.

Advantages of Binary Search Trees

1. Unlike Binary Search, which works only for a fixed data set, Binary Search Trees can be used for dynamic data sets as well.
2. It can be used to find the sorted order of a dynamic data set.
3. If elements are inserted/deleted randomly, it is actually faster to do it in a binary search tree than in linked lists and arrays.
4. We can actually calculate a lot more stuff using a Binary Search Tree like the floor and ceiling values for any element.

Disadvantages of Binary Search Trees

1. The overall shape of the tree depends on the order of insertion. If data is inserted in a sorted order or the tree becomes heavier(skewed) in one direction, the insert/search operations become expensive.
2. A lot of space is required as we need to store the left and right child of each node.
3. The plain implementation of Binary Search Tree is not much used since it cannot guarantee logarithmic complexity. Hence, we have to use self balancing implementations which are a bit more complex to understand and implement.

Conclusion

Today we discussed a pretty awesome algorithm which can put Binary Search to shame 😛 It provides logarithmic complexity for insertions and search if the data set is randomised and dynamic.

Thanks for reading. May the code be with you 🙂