Binary Exponentiation is a technique of computing a number raised to some quantity, which can be as small as $0$ or as large as $10^{18}$ in a fast and efficient manner. It utilises the property of exponentiation and the fact that any number can be represented as sum of powers of two depending on its binary notation to get an edge over the naive brute force method.

Scope of article

• This article explains what is binary exponetiation, where it can be used and it’s implementation.
• This article shows the implementation of binary exponentiation in C++ only.

Takeaways

• Complexity of Binary exponentiation
  • Time complexity – $O(log(b))$

Introduction of Binary Exponentiation

Exponentiation means raising a number to a power. If we raise $’a’$ to the power $’b’$, it means we multiply $a$ with itself $b$ times.

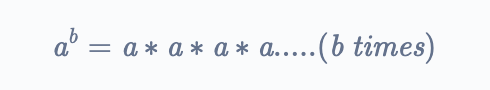
If we look carefully at the definition, it means that to find a raised to the power of b or $a^b$, we would need to perform the muliplication operation b times.

There can be two ways to compute exponentiation : iterative method by using a for loop or by using recursion. Let us see both of these methods in detail.

Iterative Way

In this method, we use a for loop to multiply a with itself b times. As we use a for loop to iterate b times, it is called the iterative method.

#include <iostream>
using namespace std;

int main() {

    // we need to compute a^b
    int a = 4, b = 8;

    // this will contain the final answer
    int answer = 1;

    // the for loop iterates b times
    for(int i=1; i<=b; i++){

        // we multiply answer with a for each iteration
        answer = answer*a;

    }

    // answer contains required a^b
    cout<<"4 raised to the power 8 is : "<<answer<<endl;

    return 0;
}

Output

4 raised to the power 8 is : 65536

As we can see in the above code, the for loop runs a total of $b$ times, and each time we multiply answer with $a$, so that in the end answer variable contains $a$ multiplied $b$ times or $a^b$.

The for loop runs $b$ times, so the complexity of above code is $O(b)$, where $b$ is the exponent or the power the number is being raised to.

Recursive Way

In this method, we use recursion to compute $a^b$. Recursion is a function calling itself with smaller parameters until a base condition is reached. For exponentiation, the base condition will be when $b = 0$. In such a case we just return 1, in all other cases, we multiply the answer by $a$, and recurse for $b-1$.

#include <iostream>
using namespace std;

int exponent(int a, int b){

    // base case, when b = 0
    if(b==0){
        // any number raised to 0 is always 1
        return 1;
    }

    //else we recurse for b-1 after multiplying the answer with a and return the answer

    // now answer stores a^b
    int answer = a * exponent(a,b-1);

    return answer;
}
int main() {

    // we need to compute a^b
    int a = 4, b = 8;

    // call the recursive function to compute a^b
    cout<<"4 raised to the power 8 is : "<<exponent(a,b)<<endl;

    return 0;
}

Output

4 raised to the power 8 is : 65536

In this case, we recurse until $b$ becomes 0, that means we call the recursive function a total of $b$ times, making the complexity $O(b)$ in this case also.

So, this makes the time complexity of exponentiation as $O(b)$, where $b$ is the exponent or the power the number is being raised to.

Now, if $b$ is of the order of $10^9$ or $10^{18}$, then it means the code described above will run for a total of $10^9$ or $10^{18}$ times, which is a lot!

So, when dealing with large values of $b$, this algorithm is much expensive and time consuming. This is where Binary Exponentiation comes into the picture.

Why Binary Exponentiation?

If we can somehow find a way to make our exponentiatio

If we can somehow find a way to make our exponentiation faster, we would be able to compute $a^b$ for large values of $b$ also. This is exactly what Binary Exponentiation does.

By using Binary Exponentiation, we can compute $a^b$ in only $O(log(b))$ operations. That means we now only need to perform $O(log(b))$ multiplications to find out the value of $a^b$. We will explore more about the time complexity of binary exponentiation in detail after we define it in the next sections.

Let us explore the intuition behind Binary Exponentiation and also its algorithm in the next section.

Algorithm

How does Binary Exponentiation achieve logarithmic time complexity?

Let us explore the intuition behind the algorithm before we define it.

Intuition

Binary Exponeniation uses the property of exponentiation and the fact that any number can be represented as sum of powers of two depending on its binary notation, to compute the final answer.
According to the property of exponentiation,

$$
a^b = a^c * a^d \ ,
if \ \ b = c + d
$$

This means, that if we want to compute $a^b$ and we have already computed values of $a^c$ and $a^d$, we require only one multiplication operation to get the final answer to $a^b$.

Now if we look at b in its binary representation, we will be able to write b as a sum of powers of two.

As an example let us take a = 5 and b = 12.
12 in binary is represented as :

$$
12 = 1100
$$

In powers of two, we can re-write it as

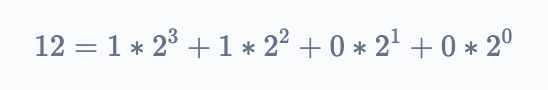
In other words 12 can be represented as a sum of $2^3$ and $2^2$.

So, if we want to compute $a^b$ with a = 5 and b = 12, we can rewrite it as :

$$
5^{12} = \ 5^{2^3 + 2^2} =\ 5^{2^3}*5^{2^2}
$$
$$
5^{12} = 5^8 * 5^4
$$

In other words, the problem boils down to representing $b$ as the sum of powers of two and then computing $a$ raised to only those powers of two and multiplying them together.
Like, here as 12 can be expressed as a sum of $2^3$ and $2^2$, we only need to compute $5^8$ and $5^4$ and multiply them together to get to the final answer.

But here again, computing $5^4$ requires 4 operations, and computing $5^8$ requires eight operations. Combining this with one operation to multiply them together, we get a total of (4+8+1) = 13 operations, which is not an improvement over the previous method.

The thing to notice here is that now we have to only compute $a^{\ some \ power \ of \ two}$ and then multiply them together. We can use this to our benefit in the sense that if we have $a$ raised to a power of two, say $a^x$ computed, where x is a power of two, to compute $a^y$, where $x<y$ and $y$ is also a power of two, we don’t need to start from scratch, we can instead keep multiply $a^x$ with itself to get the next power of two, and keep doing this until we reach $a^y$.

This follows directly from one other property of exponents, which is :
$$
(a^b)^c = a^{b*c}
$$

So, if we have $a^b$ computed where b is a power of two, then to get the value $a$ raised to the next power of 2, we just need to compute $(a^b )^2$, which requires only one multiplication operation, which is $a^b * a^b$. This way we can get the required $a^{\ some \ power \ of \ two}$ and multipying them together will give us the final answer.

Consider the previous example of $a=5$ and $b=12$, we already saw we need to multiply $5^4$ and $5^8$. Now, instead of computing $5^4$ by multipying $5$ four times, we instead start computing 5 raised to powers of 2 starting from 0. So, we compute $5^{2^0}$, then $5^{2^1}$ by multiplying the previous values together and so on.

$$
5^1 = 5
$$
$$
5^2 = (5^1)^2 = 5^2 = 25
$$
$$
5^4 = (5^2)^2 = 25^2 = 625
$$
$$
5^8 = (5^4)^2 = 625^2 = 390625
$$

Hence, we can compute the values of $5^4$ and $5^8$ in 4 operations and only one more operation (multiplying $5^4$ and $5^8$) is needed to get the final answer.

$$
5^{12} = 5^4 * 5^8 = 625 * 390625 = 244140625
$$

Time Complexity

So, we get to the final answer in just 5 operations, as opposed to 12 operations if we did the exponentiation the brute force way.

The final complexity of this algorithm turns out to be $log(b)$ , because atmost all bits in the binary representation of $b$ will be set, so we will have to compute $a$ raised to atmost $log(b)$ power of 2, and multiplying them together will take more $log(b)$ operations.

Hence, the overall complexity is $O(log(b))$ , where b is the exponent.

Actual Algorithm

So, we start by computing $a$ raised to $2^0$ , i.e, $a^1$, then multiply these together to get $a^2$ ,then multiply these together to get $a^4$ and so on. But, we multiply in the answer only those values of $a^{ \ some \ power \ of \ 2}$ whose bits in $b$ are set, as they will be the only ones that sum upto $b$, as discussed above.

To know if the nth bit in $b$ is set, we can use $AND$ with 1 bit shifted by n, i.e, $1<<n$ and check if the result is non-zero. Conversely, we can keep dividing $b$ by 2 during iterations and just find out its remainder every time to check if the bit is set or not. This is equivalent to converting $b$ into its binary representation.

Note in the algorithm, that we only multiply $a$ in the answer when the bit is set, as only those values of $a^{ \ some \ power \ of \ 2}$ sum upto $b$.

The algorithm to compute $a^b$ is :

POWER(a,b) :
    if b==0 :{
        return 1
    }
    else if b is odd :{
        //this bit is set in binary representation of b as remainder will be 1
        return a*POWER(a,(b-1)/2)*POWER(a,(b-1)/2)
    }
    else :{
        //this bit is not set in the binary representation of b as remainder is 0
        return POWER(a,b/2)*POWER(a,b/2)
    }   

This algorithm can be implemented by recursion as well as in the iterative method. Both of these have been described in detail in the next section.

Implementation of Binary Exponentiation

There are two approaches to the above defined algorithm, both of which we will discuss in detail in this section.

Recursive Approach

A recursive approach is one in which the recursive function calls itself with slightly smaller parameter, until the base case is reached.

For binary exponentiation, our base case will be when our exponent, i.e b in $a^b$, turns 0. In such a case, we simply return 1 irrespective of a.

For all other cases, we follow the algorithm defined above. If the current bit in b is set, that is if b leaves a remainder of one when divided by two, then we recurse for (b-1)/2 and multiply it twice with a and return it. Else, b gives a remainder zero when divided by 2 and hence the current bit is unset, so we just recurse for b/2 and multiply it twice and return it.

“`cpp

include

using namespace std;

//recursive function to calculate a^b
int power (int a, int b){
//base case
if(b==0){
return 1;
}
//if b is odd
else if(b%2==1){
return apower(a,(b-1)/2)power(a,(b-1)/2);
}//if b is even
else{
return power(a,b/2)*power(a,b/2);
}
}
int main() {

//the exponent to be calculated
int a = 5 , b = 12;

//output the answer
cout<<"5 raised to the power 12 is : "<<power(a,b)<<endl;

return 0;

}

### Iterative Approach

In the `iterative approach` we follow the same logic, but without recursion. Instead, we use a while loop to perform the same operations, until `b` is greater than `0`.

cpp

include

using namespace std;

int main() {

// the exponent we want to calculate
int a = 5 , b = 12;

//we will store the answer in this variable
int answer = 1;

//iterate till b>0
while(b>0){

    //if b is odd, then this bit is set
    if(b%2==1){
        //in this case, multiply the current power of a to the answer
        answer = answer*a;
        //compute the sqaure of current a
        a = a*a;
    }
    //b is even, so the current bit is not set
    else{
        //in this case, we dont need to multiply anything to the answer
        //we just compute the sqaure of a
        a = a*a;
    }

    //the current bit has been analysed, we move to the next bit
    //so we divide b by 2
    b = b/2;

}

//output the answer
cout<<"5 raised to the power 12 is : "<<answer<<endl;

return 0;

}
“`

The time complexity of both these solutions is the same and equal to $O(log(b))$ , though the recursive solution has an overhead of recursive calls.

Applications

• In cryptography, large exponents with modulo of a number are widely used. To compute large exponents, binary exponentiation is a fast method which finds an application in this field.
• We can efficiently compute large exponents modulo some large number by this technique. This particular application is useful in solving many mathematical problems.
• This can be used to computemodular multiplicative inverse of a number.
• Basically, this method is very useful for problems where we need to compute exponentiation in a speedy fashion.

Conclusion

• Binary Exponentiation is a technique of computing a number raised to some quantity in a fast and efficient manner.
• It uses properties of exponentiation and binary numbers for fast computation.
• It has time complexity of O(log(b)) where b is the power any number is being raised to.
• It finds its applications in cryptography and in other mathematical problems where computation of exponents is required.

Ignite Data Structures Brilliance! Enroll in Scaler Academy’s Online DSA Course to Hone Your Coding Skills.