The Bellman-Ford algorithm is an example of Dynamic Programming. It starts with a starting vertex and calculates the distances of other vertices which can be reached by one edge. It then continues to find a path with two edges and so on. The Bellman-Ford algorithm follows the bottom-up approach.
What is Bellman-Ford Algorithm?
The Bellman-Ford algorithm computes the shortest path from a source vertex to all others in a graph, accommodating both weighted and unweighted edges. While it’s generally slower than Dijkstra’s method, Bellman-Ford excels in graphs with negative edge weights and detects negative cycles, a crucial feature. This capability prevents infinite loops where path costs decrease infinitely by traversing negative cycles. Utilizing dynamic programming, Bellman-Ford employs a bottom-up approach, iteratively refining distance estimates via the “Principle of Relaxation.” Starting with immediate neighbors, it progressively evaluates longer paths, converging to the optimal solution. However, if negative weight cycles exist, they can distort path distances, necessitating caution during analysis. Thus, Bellman-Ford offers a robust, albeit slower, alternative for diverse graph scenarios.
Example of Bellman Ford Algorithm
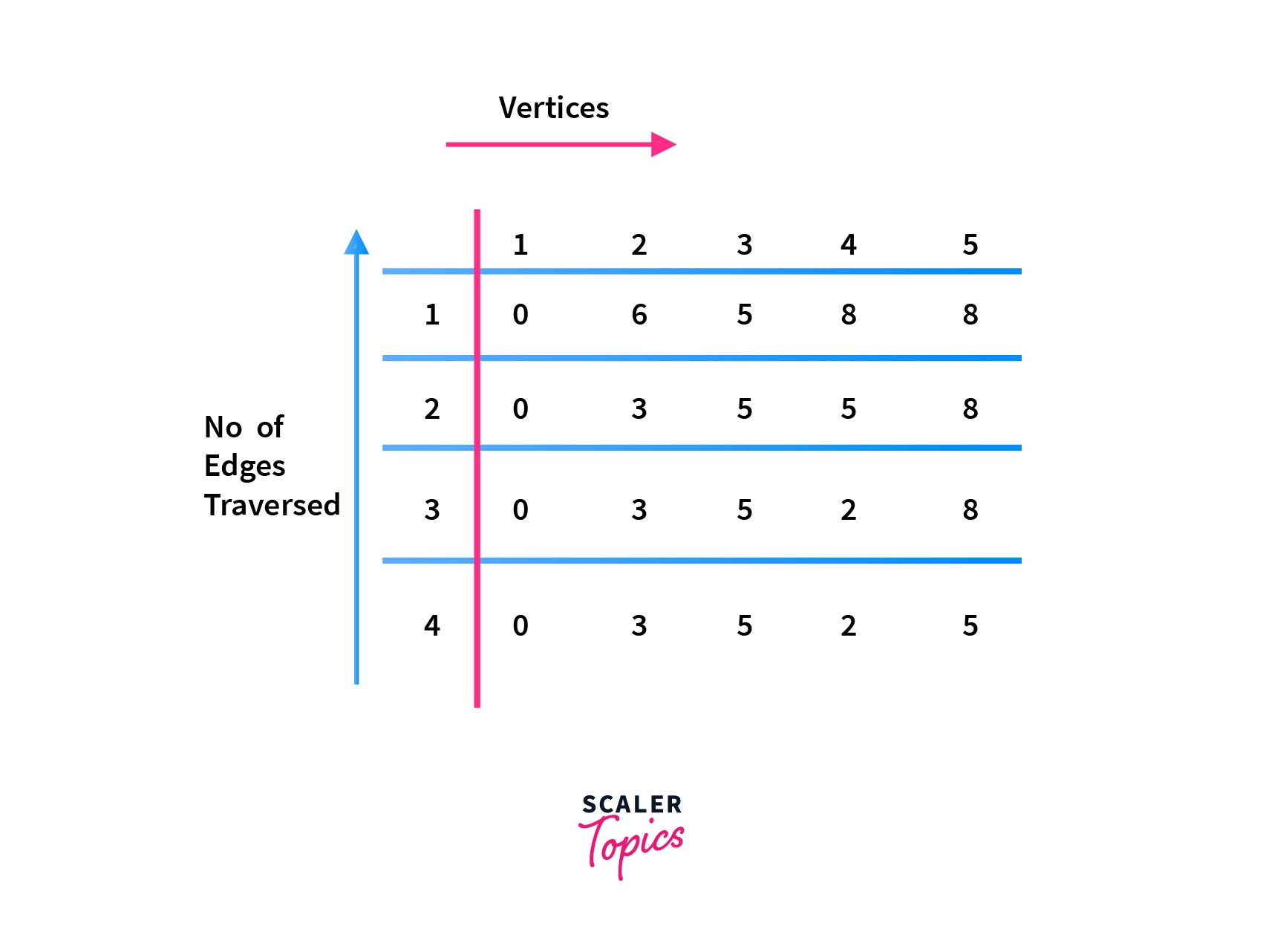
Suppose that we have a graph consisting of 5 vertices having edges between them as shown in the picture below. Now, we want to find shortest distance to each vertex vi 0 starting from the vertex 1.

After performing bellman ford algorithm on the above graph the output array would look like –Shortest_Distance = [0, 3, 5, 2, 5]
Where each index 'í' of array denotes the shortest distance of the ith vertex from 1st vertex, 1<=i<=5.
How Bellman Ford Algorithm Works?
The algorithm works by iteratively relaxing the edges of the graph to find the shortest path.
Here are the step-by-step workings of the Bellman-Ford algorithm:
Step 1: Initialize distances and predecessors
The algorithm starts by initializing the distance of the source node to 0 and the distances of all other nodes in the graph to infinity.
for i in range(0, |V|):
distance[i] = infinite
distance[src] = 0Step 2: Relax edges
The algorithm then iteratively relaxes the edges of the graph. For each edge u→v with weight w, it checks if the distance to v can be improved by going through u. If the distance can be improved, it updates the distance of v and sets its predecessor to u.
def relax_edges(u, v):
if distance[v] > distance[u] + weight_of_edge(u --> v):
distance[v] = distance[u] + weight_of_edge(u --> v) Above step is repeated V-1 times for every edge.
for _ in range(V):
for (u, v) in edges:
relax_edges(u, v)Step 3: Check for negative cycles
After all the edges have been relaxed, the algorithm checks for negative cycles in the graph. A negative cycle is a cycle whose total weight is negative. If there is a negative cycle in the graph, the algorithm reports it and terminates. Step 2 (relax edges) is repeated one more time for all the edges. If there is some edge some which can be further relaxed then we say that there is an negative cycle present in the graph.
for (u, v) in edges:
if dis[v] > dis[u] + weight[u --> v]:
print("negative cycle present")
breakStep 4: Shortest paths
If there are no negative cycles in the graph, the algorithm returns the shortest path from the source node to every other node in the graph.
dis[i] - gives the shortest distance from src node to node i. Input:
- A 2D Array/List denoting edges and their respective weights.
- A src vertex.
Output:
An array where each index denotes the shortest path length between that vertex and src vertex.
Procedure:
- In this step, we would declare an array of size
V(Number of vertexes) saydis[]and initialize with all of its indexes with a very big Value (preferablyINT_MAX) except src which will be initialized with value0.
We are doing this because initially we assume that it takes infinite time to reach any of the vertices from our source vertex and we are initializing dis[src]=0 because we are already on source vertex. - In this step, the shortest distance is calculated. For it, we would do the underlying step
V-1times.
For every edge u→v make
dis[v]=min(dis[u]+ wt of edge _u→v, dis[v])_
It means whenever we are on any vertex u we will check if we can reach any of its neighbors in less time it is currently possible to visit, we will update the dis[v] to dis[u]+wt of edge u→v. - In this step, we will check if there exists a negative edge weight cycle traversing each and every edge u→v and checking if there exists
dis[u] + wt of edge _u→v < dis[v]_
then our graph contains a negative edge weight cycle because traversing the edges again and again is beneficial as it is lowering the cost to traverse the graph. –>
Explanation of Bellman Ford Example
Boost Your Tech Profile! Join Our DSA Courses for Advanced Algorithmic Mastery. Enroll Now to Stand Out in the Coding Landscape!
Difference between Dijkstra’s and Bellman Ford’s Algorithm
| Bellman Ford Algorithm | Dijkstra Algorithm |
|---|---|
| Its implementation is inspired by the dynamic programming approach. | Its implementation is inspired by the greedy approach. |
| It is easier to implement in a distributive way. | It is quite complex to implement in a distributed way. |
| It also works when the given graph contains a negative edge weight cycle. | It fails if a graph contains a negative edge weight cycle. |
| It’s is more time consuming than Dijkstra’s. It’s Time complexity is O(VE) | It’s Time complexity is O(ELogV) |
Pesudocode
BellmanFord(Edges[][], src, V):
dis[] = new int[V]
For i = 1 to V :
dis[i] = INF // (INF=Very Large Value)
dis[src] = 0
For i = 1 to V-1 :
For j 1 to Edges.length:
u = Edges[j][0]
v = Edges[j][1]
wt = Edges[j][2]
dis[v] = MIN(dis[u]+wt,dis[v])
For i = 1 to Edges.length:
u = Edges[i][0]
v = Edges[i][1]
wt = Edges[i][2]
If(dis[v] > dis[u]+wt)
Print "Negative Weight cycle exists."
Return disCodes Implementation of Bellman Ford Algorithm
- ### C/C++ Implementation of
Bellman Ford
vector<int> bellmanFord(vector<vector<int>>,int src, int V){
// Step 1 - Creating a V sized array/vector,
// and initializing it with a very big value.
vector<int> dis(V,INT_MAX); // Creating a vector dis of size V with values as INT_MAX.
dis[src] = 0; // Since we are already on source vertex, we can reach it within no time.
// Step 2 - For V-1 times, traversing over,
// all the edges and checking if a shorter
// path between any edge u to v is possible.
int u,v,wt;
for(int i=0;i<V-1;i++) // Iterating V-1 times
{
for(int j=0;j<edges.size();j++) // Iterating over all the edges.
{
u = edges[j][0]; // Source vertex.
v = edges[j][1]; // Destination vertex.
wt = edges[j][2];// Weight of the edge.
// If we can reach v from u in less time it
// is currently required to reach v then update
// the value.
if(dis[u]!=INT_MAX && dis[v] > dis[u] + wt)
dis[v] = dis[u] + wt;
}
}
// Step 3 - Checking for negative edge weight cycle,
// by checking if the underliying condition satifies.
for(int j=0;j<edges.size();j++)
{
u = edges[j][0];
v = edges[j][1];
wt = edges[j][2];
// If the below condition satisfies, it means negative
// edge weight cycle exists. Because traversing again
// is reducing the cost and in order to minimize the
// cost we can traverse till infinity and hence a proper
// answer can't be calculated.
if(dis[u]!=INT_MAX && dis[v] > dis[u] + wt)
return {};
}
return dis; // returning our answer vector/array.
}- ### Java Implementation of Bellman Ford
int[] bellmanFord(int edges[][],int V,int src){
// Step 1 - Creating a V sized array/list,
// and initializing it with a very big value.
// Creating a vector dis of size V with values as INT_MAX.
int dis[]=new int[V];
Arrays.fill(dis,Integer.MAX_VALUE);
dis[src]=0; // Since we are already on source vertex, we can reach it within no time.
// Step 2 - For V-1 times, traversing over,
// all the edges and checking if a shorter
// path between any edge u to v is possible.
int u,v,wt;
for(int i=0;i<n-1;i++) // Iterating V-1 times
{
for(int j=0;j<edges.length;j++) // Iterating over all the edges.
{
u=edges[j][0]; // Source vertex.
v=edges[j][1]; // Destination vertex.
wt=edges[j][2];// Weight of the edge.
// If we can reach v from u in less time it
// is currently required to reach v then update
// the value.
if(dis[u]!=Integer.MAX_VALUE&&dis[u]+wt<dis[v])
dis[v]=dis[u]+wt;
}
}
// Step 3 - Checking for negative edge weight cycle,
// by checking if the underliying condition satifies.
for(int j=0;j<edges.length;j++)
{
u=edges[j][0];
v=edges[j][1];
wt=edges[j][2];
// If the below condition satisfies, it means negative
// edge weight cycle exists. Because traversing again
// is reducing the cost and in order to minimize the
// cost we can traverse till infinity and hence a proper
// answer can't be calculated.
if(dis[u]!=Integer.MAX_VALUE&&dis[u]+wt<dis[v])
return new int[0];
}
return dis; // returning our answer vector/array.
}- ### Python Implementation of Bellman Ford
def bellmanFord(V,edges,src):
# Step 1 - Creating a V sized array/list,
# and initializing it with a very big value.
INF=999999999
dis=[INF for x in range(V)]
dis[src]=0 # Since we are already on source vertex, we can reach it within no time.
# Step 2 - For V-1 times, traversing over,
# all the edges and checking if a shorter
# path between any edge u to v is possible.
for i in range(V-1): # Iterating V-1 times
for j in range(len(edges)): # Iterating over all the edges.
u=edges[j][0]; # Source vertex
v=edges[j][1]; # destination vertex
wt=edges[j][2]; # weight of edge from u to v
# If we can reach v from u in less time it
# is currently required to reach v then update
# the value.
if(dis[u]!=INF and dis[u]+wt<dis[v]):
dis[v]=dis[u]+wt
# Step 3 - Checking for negative edge weight cycle,
# by checking if the underliying condition satifies.
for i in range(len(edges)):
u=edges[i][0];
v=edges[i][1];
wt=edges[i][2];
# If the below condition satisfies, it means negative
# edge weight cycle exists. Because traversing again
# is reducing the cost and in order to minimize the
# cost we can traverse till infinity and hence a proper
# answer can't be calculated.
if(dis[u]!=INF and dis[u]+wt<dis[v]):
return []
return dis # Return our answer array/listComplexity Analysis of Bellman Ford
Time Complexity– Since we are traversing all the edges V-1 times, and each time we are traversing all the E vertices, therefore the time complexity is O(V.E).- ####
Space Complexity–
Since we are using an auxiliary array dis of size V, the space complexity is O(V).Where V and E are numbers of vertices and edges respectively.
Bonus Tip of Bellman-Ford Algorithm
The algorithm can be speeded up further because in most of the cases we get our final answer after performing step 2 few times only. Because dis array stops getting updated after some steps, So traversing edges again and again is nothing but waste of time.
To check wether any value of dis gets updated in any given iteration, we can keep a flag in the outer loop of Step 2 and if it not changed in the inner for loop then we can exit from the loop becuase we have already got our answer.
Though the modification will not change the asymptotic nature of the algorithm because in some graphs we will need all the V-1 steps to be done. But it will optmize the run time of algorithm in a “average case” i.e. random graphs.
The minor modification need to be done in step 2 is given below –
for(int i=0;i<n-1;i++)
{
boolean flag=true;
for(int j=0;j<edges.length;j++)
{
u=edges[j][0]; // Source vertex
v=edges[j][1]; // Destination vertex
wt=edges[j][2];// wight of edge from u to v.
// If we can reach v from u in less time it
// is currently required to reach v then update
// the value.
if(dis[u]!=Integer.MAX_VALUE&&dis[u]+wt<dis[v])
{
dis[v]=dis[u]+wt;
// Make flag false since we have entered in
// the if conditon which maens there will be
// at least one updation in next araay.
flag=false;
}
}
// If flag is still true it means
// condition did not satisfied even once.
if(flag)
break;
}Though the average case Time Complexity would be – O(V.E) but in the best case it can be done in only O(E) time. Think of the case in which we get out of the loop after the very first or second step.
Applications
- Checking for negative edge weight cycle.
- For finding shortest path of all vertices from single source.
- Routing Algorithms.
Join our expert-led Dynamic Programming Free Course to master advanced problem-solving techniques and enhance your programming prowess.
Conclusion
- In this blog, we have discussed one of the most important graph algorithms i.e.
Bellman-Ford algorithmwhich is used to find the shortest path to all vertices from a single source vertex inO(VE)time complexity. - It can find shortest distance of all vertices from single source. It can also detect if there exists a negative edge weight cycle in the given graph. Therefore, it also finds its way in many routing techniques.
- If you want to upskill yourself in Data Structures and algorithms then do checkout, Scaler where you will get live lectures, assignments, and regular tests from the people working in your dream company.