Backtracking Algorithm

Backtracking is an improvement of the bruteforce approach. It tries to search for a solution to a problem among all the available options. It finds a solution set by developing a solution step by step, increasing levels with time, using recursive calling.

Takeaways

Backtracking is a general algorithm for finding solutions to some computational problems, notably constraint satisfaction problems, that incrementally builds candidates to the solutions.

Introduction to Backtracking Algorithm

• In backtracking, we always start with one possible choice out of many available choices and try to find out the solution of the problem if we are able to find the solution with the selected move then we will print the solution else we will backtrack and select some other option and try to solve the problem.
• It allows us to deal with situations in which a brute-force approach would lead to an impossible number of choices to consider.

So in the backtracking algorithm at each node, we try to eliminate the choices that are not possible and proceed further to recursively check only those choices that can contribute towards the solution.

How Backtracking Algorithms Works?

Backtracking is the technique to solve programs recursively. In backtracking problems, you will have a number of options and you must choose one of these options.

After you make your choice you will explore a new set of options, if you reach the feasible solution through those choices you will print the solution otherwise you will backtrack and return to explore the other paths and choices that can possibly lead to the solution.

For Instance: Consider the following space state tree. With the help of the below space state tree let’s understand how the backtracking algorithm actually works.

We start from S which is the starting point of our problem. We go to find a solution to Y1 from intermediate point X1 and then we find that Y1 is not a feasible solution to our problem therefore we backtrack and go back to X1 via Y1 then go back to S and then again try to find out the feasible solution by following another path S->X2->Y2 and again we will find that Y2 is not a feasible solution so we will again return to S by following path Y2->X2->S and then we will ultimately reach out to feasible solution Y3 by following the path S->X3->Y3.

So we can summarise the backtracking algorithm as follows:

1. We select one possible path and try to move forward towards finding a feasible solution.
2. If we will reach a point from where we can’t move towards the solution then we will backtrack.
3. Again we try to find out the feasible solution by following other possible paths.

When to Use a Backtracking Algorithm?

Backtracking algorithms are ideally used when solving problems that involve making a sequence of choices, with each choice leading towards a potential solution. They are best suited for problems where the solution space is large and a brute-force approach is computationally impractical. This includes puzzles like Sudoku or the N-Queens problem, and decision-making problems such as finding shortest paths, subsets, or combinations. However, backtracking may not be optimal for problems with smaller decision spaces or those that can be solved more efficiently with other algorithms.

Types of Backtracking Problems

Before start solving the problem we must be able to recognize if it can be solved using a backtracking algorithm. There are the following types of problems that can be solved using backtracking:

1. Decision Problem: In this type of problem we always search for a feasible solution.
2. Optimization Problem: In this type of problem we always search for the best possible solution.
3. Enumeration Problem: In this type of problem we try to find all feasible solutions.

Example of Backtracking Algorithm

We will discuss N Queen example which is a very popular problem that can be solved using Backtracking.
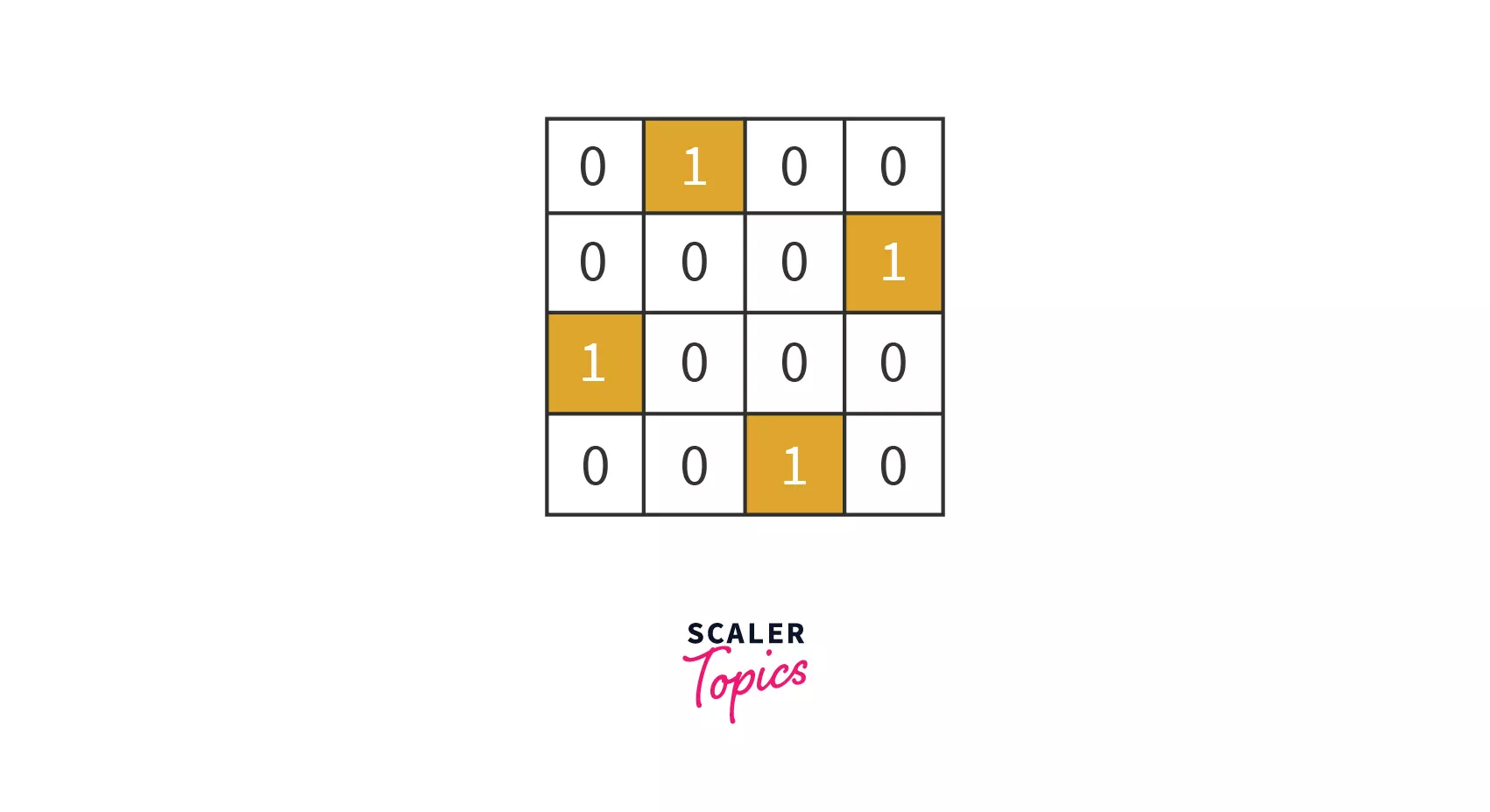
In the N Queen problem, we have to place N queens on an N×N chessboard such that no two queens can attack each other. We cannot place two queens in the same row or same column or same diagnol in order to avoid the attack. For instance, given below is the configuration for placing N queens on N*N chessboard where N=4.

In the output, we will print the binary matrix containing 1s where the queen can be placed, and the rest all cells will contain 0s.

Solution: The bruteforce approach of solving this problem is generating all possible configurations of queens on board and then printing the configuration which will satisfy the constraint. But the time complexity of this approach will be exponential as we have to generate all possible configurations. But we can improve the time complexity by using a backtracking algorithm.

In the backtracking algorithm, we will start from the leftmost column and one by one try to place queens in different columns. When we place a queen in a column, we will check if the queen that we have placed currently is clashing with other already placed queens. In the current column, if we are able to find a row for which it is safe to place a queen then we will mark this row and column as part of the solution. If we do not find such a row due to clashes then we will backtrack and return false.

Approach to Code: We will have a chessboard in the form of a 2d matrix in which we will try to place the queens. We will create the following three functions:

• solveNQueen(): This will be the recursive function to solve n queen problem. It will take two arguments, a board matrix, and a column number.
• isSafe_to_place(): This function will check if it is safe to place the queen in the current cell. It will take arguments board matric, current row, and current column.
• printOutput(): This function will print the output matrix.

Below is the C++ implementation of the above approach:

/* C++ program to solve N Queen Problem */
#define N 4
#include <bits/stdc++.h>
using namespace std;

  /* A function to check if a queen can
   be safely placed on board[row][col]. */
bool isSafe_to_place(int board[N][N], int row, int col)
{
    int i, j;

    /* Checking this row on left side */
    for (i = 0; i < col; i++)
        if (board[row][i])
            return false;

    /* Checking upper diagonal on left side */
    for (i = row, j = col; i >= 0 && j >= 0; i--, j--)
        if (board[i][j])
            return false;

    /* Checking lower diagonal on left side */
    for (i = row, j = col; j >= 0 && i < N; i++, j--)
        if (board[i][j])
            return false;

    return true;
}

/* A recursive function to solve N
   Queen problem */
bool solveNQueen(int board[N][N], int col)
{
    /* base case: If all queens are placed
      then return true */
    if (col >= N)
        return true;

    /* Consider this column and try placing
       this queen in all rows one by one */
    for (int i = 0; i < N; i++) {
        /* Check if the queen can be placed on
          board[i][col] */
        if (isSafe_to_place(board, i, col)) {
            /* Place this queen in board[i][col] */
            board[i][col] = 1;

            /* recur to place rest of the queens */
            if (solveNQueen(board, col + 1))
                return true;

            /* If queen cannot be placed then simply backtrack 
                and try other configurations */
            board[i][col] = 0; // BACKTRACK
        }
    }

    /* If the queen cannot be placed in any row in
        the current column then return false */
    return false;
}

/*  function to print output solution */
void printOutput(int board[N][N])
{
    for (int i = 0; i < N; i++) {
        for (int j = 0; j < N; j++)
            cout<<board[i][j];
        cout<<"\n";
    }
}

/* This function solves the N Queen problem using
   Backtracking. */
bool solveNQ()
{
    int board[N][N] = { { 0, 0, 0, 0 },
                        { 0, 0, 0, 0 },
                        { 0, 0, 0, 0 },
                        { 0, 0, 0, 0 } };

    if (solveNQueen(board, 0) == false) {
        cout<<"Solution does not exist";
        return false;
    }

    printOutput(board);
    return true;
}

// driver program to test above function
int main()
{
    solveNQ();
    return 0;
}    

Time Complexity: O(N!), where ‘N’ is the number of queens. For the first column, we check ‘N’ rows, for the second column, we check ‘N - 1 rows and so on. hence time complexity will be N * (N-1) * (N-2) …. i.e N!

Space Complexity: O(N^2), where ‘N’ is the number of queens. As we are using a 2-D array of size N rows and N columns, and also we will be using a recursion stack which will take linear space.

Backtracking Algorithm Applications

There are various applications of backtracking algorithms. Some of them are following:

• Maize solve the problem
• N- Queens problem
• Finding all Hamiltonian Paths present in the graph
• Subset Sum problem
• The Knight’s Tour problem
• Word break problem
• Longest possible roue in matrix with hurdles
• Word search problem

Conclusion

1. Backtracking is a technique for solving problems recursively by trying to build a solution incrementally, one piece at a time, removing those solutions that fail to satisfy the constraints of the problem at any point in time.
2. The backtracking technique is generally used in cases where there are possibilities of multiple solutions.
3. It is better than the brute force approach that tries out all the possible solutions and chooses the best possible ones out of them.