B tree is an m-way tree which self balances itself. Such trees are extensively used to organize and manage gigantic datasets and ease searches due to their balanced nature.
Takeaways
- Complexity of
B tree- Time complexity – O(log n).
Introduction to B Tree in Data Structure
Binary trees can have a maximum of 2 children while a Multiway Search Tree, commonly known as a M-way tree can yield a maximum of m children where m>2. Due to their structure, M-way trees are mainly used in external searching, i.e. in situations where data is to be retreived from secondary storage like disk files. Following is how an m-way tree looks like.
As we know, access time for secondary storage is much higher than that of primary storage, and thus our aim is to minimize the number of file accesses. To do so, the height of the tree is reduced by forming an m-way tree. Lesser the height, more efficient is the external search.
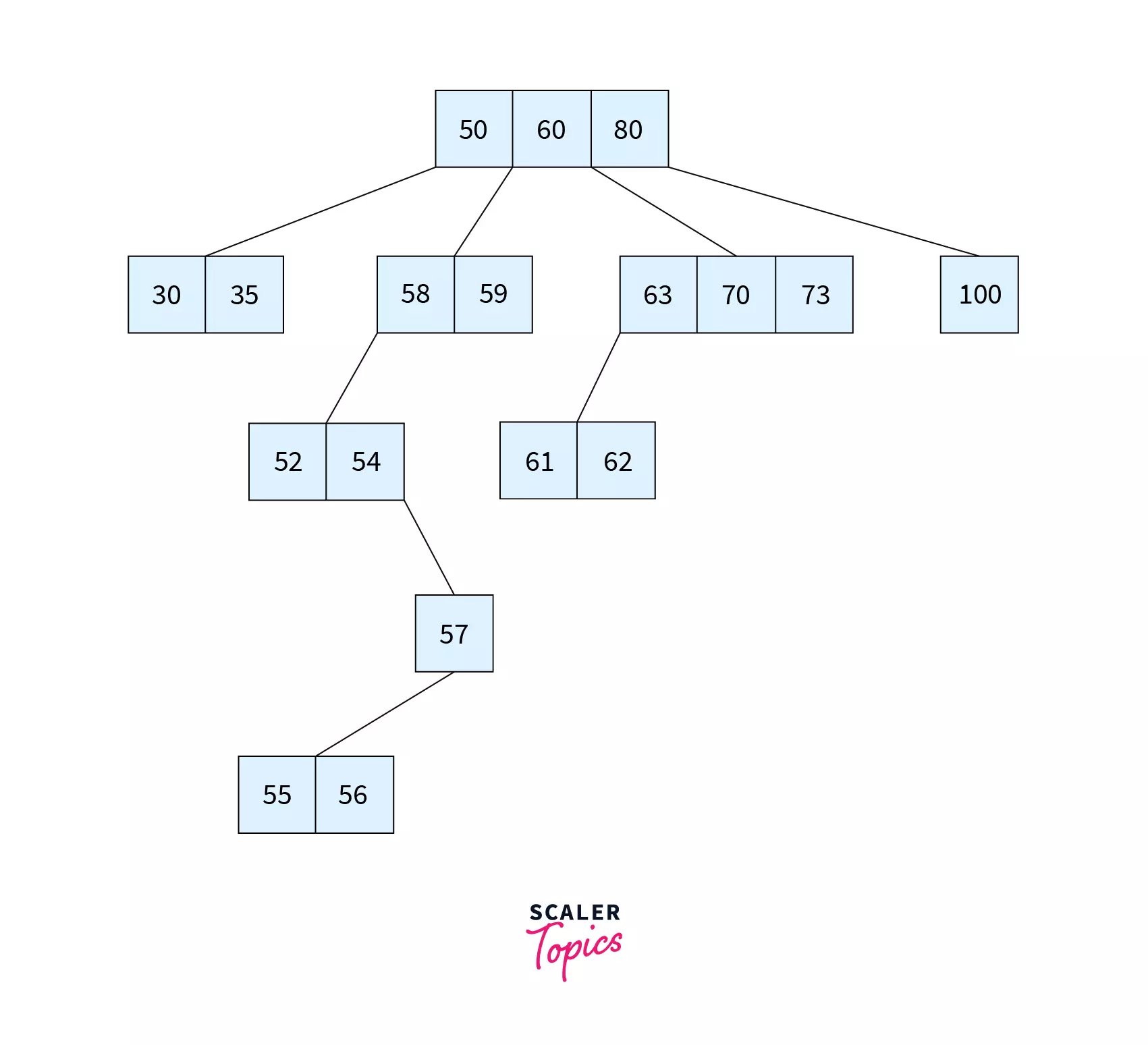
Although the height of an M-way tree is less, there is a chance for further reduction which can be achieved by balancing the tree. That’s where B tree comes in. A B Tree (height Balanced m-way search Tree) is a special type of M-way tree which balances itself.
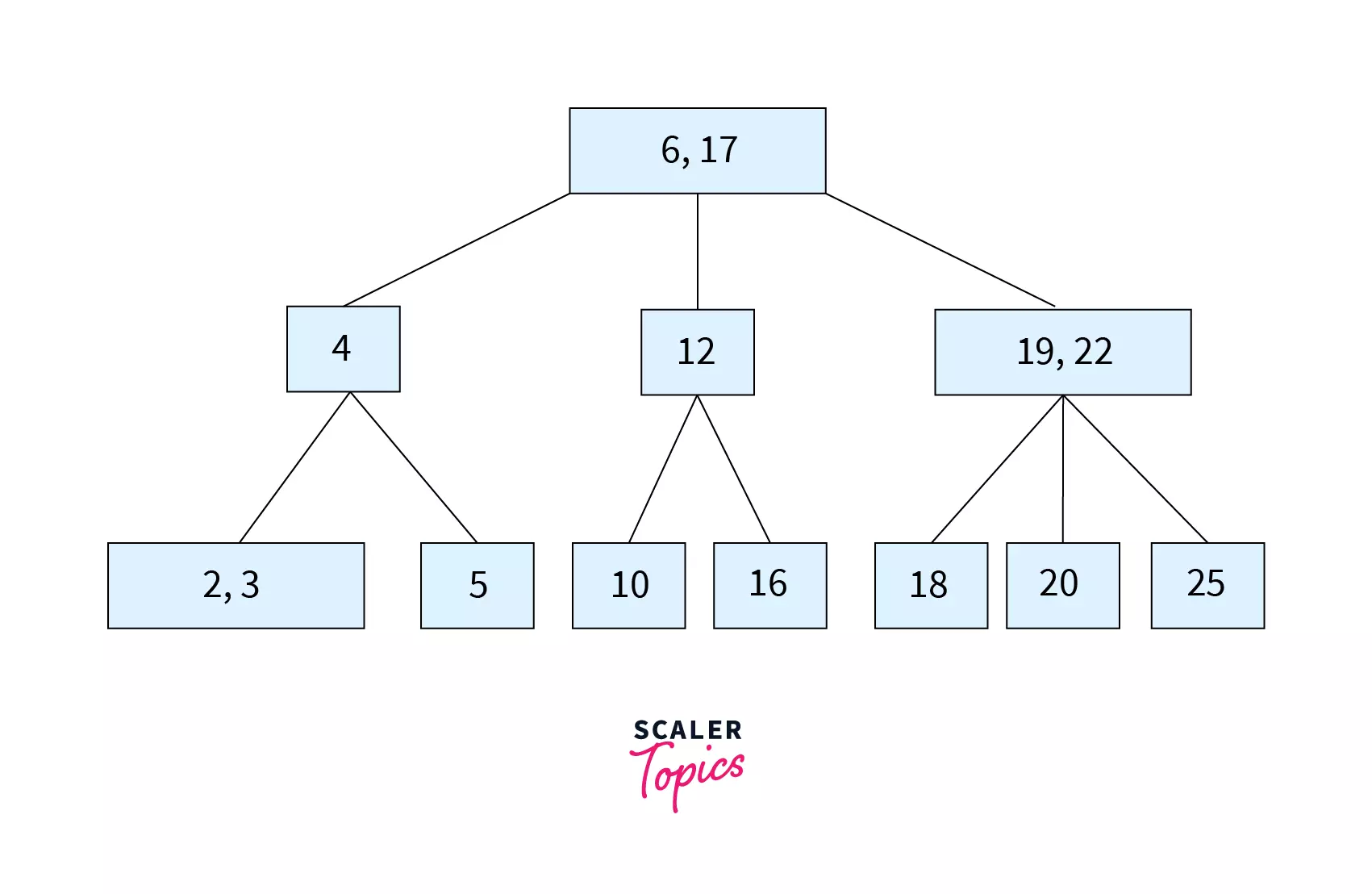
The figure above is an example of a B Tree of order 5. It has [6,17] at the root. 4 that is lesser than 6 falls in the left child. 12 being lesser than 17 and greater than 6 is the middle child. [19,22] that are greater than 17 are the rightmost child. The same process follows as we go down the tree.
Important Property of B Tree in Data Structure
A B Tree of order m can be defined as an m-way search tree which is either empty, ot satisfies the following properties:
- All leaf nodes of a
B treeare at the same level, i.e. they have the same depth (height of the tree). - The keys of each node of a
B tree(in case of multiple keys), should be stored in the ascending order. - In a
B tree, all non-leaf nodes (except root node) should have at leastm/2children. - All nodes (except root node) should have at least
m/2 - 1keys. - If the root node is a leaf node (only node in the tree), then it will have no children and will have at least on ekey. If the root node is a non-leaf node, then it will have at least
2 childrenand at least one key. - A non-leaf node with n-1 key values should have n non NULL children.
Re-read the given points while checking out the above image. As you can see, all the leaf nodes are at the same height. Each node doesn’t have multiple values mandatorily, but if it does, then they will be stored in ascending order. Eg: In the figure given, the keys are stored as [19,22] (ascending order). Considering the order of the tree of 4, so each node (except root) has at least 1 key.
From the properties, we can conclude that any node (except the root) in B tree is at least half full and this avoids wastage of space. The B tree is perfectly balanced so that the number of nodes accessed to find a key becomes less.
The value n or the order of the B tree is a degree that helps you determine the number of children a node can hold in a B tree. If the order of the B tree =3, then minimum number of children would be 2 and maximum number would be 3. Similarly, if the order of the B tree is 4, the minimum and maximum number of children would be 2 and 4 respectively.
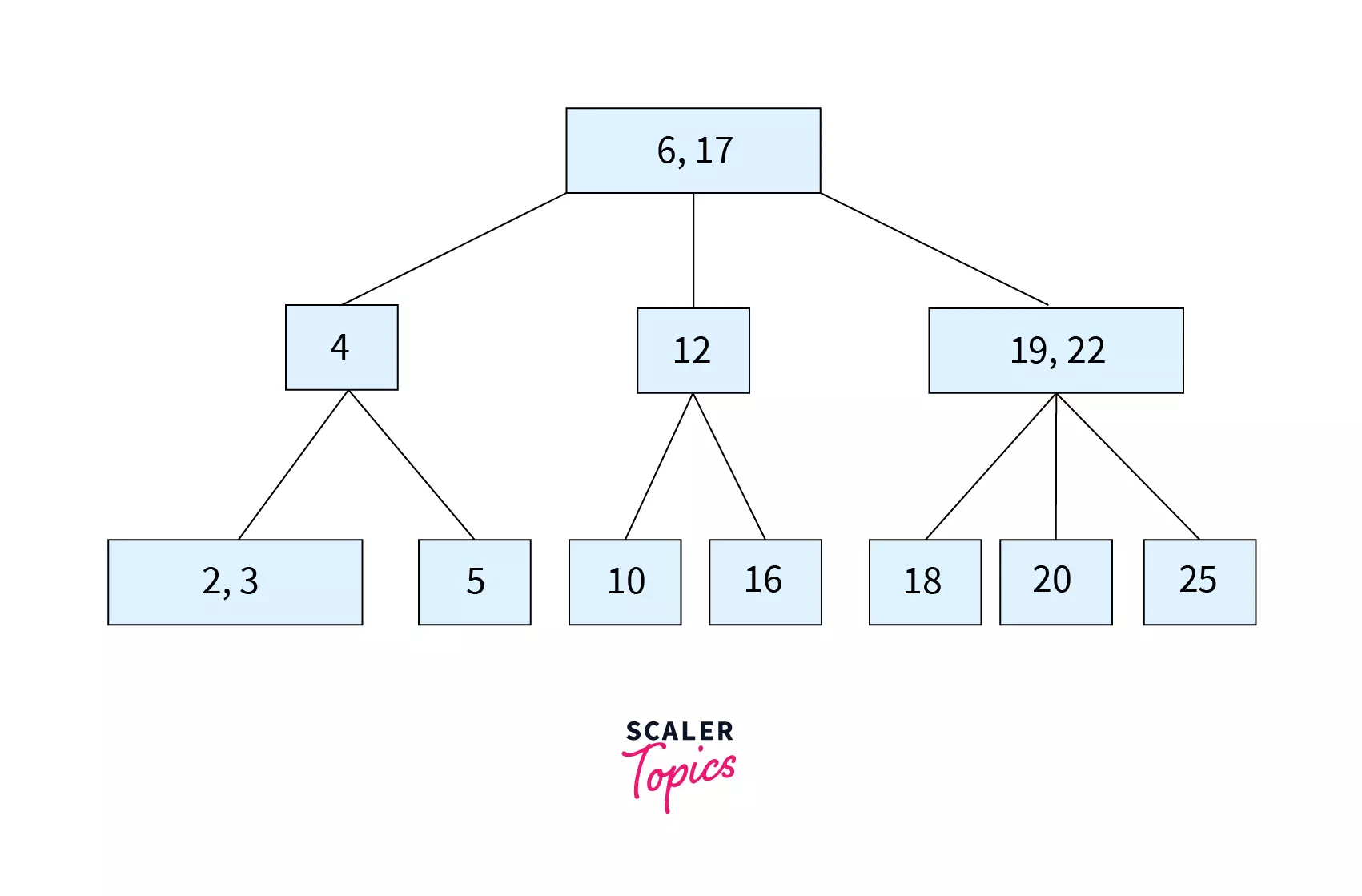
Q. Is the tree given in the following image a B Tree?
Ans: No. Since the leaf nodes are not at the same level, we can say that this is not a B Tree.
Why Do You Need B Tree Data Structure?
The B tree data structure is needed due to the following reasons:
B Treeis an extension of M-way tree. While B trees are self-balanced, M way trees can be balanced, skewed or any way. In case of external storage, there is a need for faster access. An M-way tree can help ease searches for external storage more efficiently than a normal Binary Search Tree. However, due to the self-balancing nature of a B tree, it had fewer levels and thus the access-time is cut short to a huge extent by a B Tree.- A
B treefacilitates ordered sequential access and simplifies insertion and deletion of records when there are millions of records. This is possible due to the reduced height and balanced nature of the B tree.
Operations on a B Tree in Data Structure
In order to ensure that none of the properties of a B tree are violated during the operations, the B tree may be split or joined.
Searching Operation on B Tree in Data Structure
Searching in a B Tree is similar to that in a Binary Search Tree. However, unlike a BST instead of making a 2-way decision (left or right), a B tree makes a n-way decision at each node where n is the number of children of the node.
Steps to search an element in B Tree in Data Structure
- The search starts from the root node.
Compare the search elementkwith the root.
1.1. If root node containsk, search completes.
1.2. Ifk< the first value in the root, we move to the leftmost chld and search the child recursively.
1.3.1. If the root has just2children, then move to the rightmost child and search the child recursively.
1.3.2. If the root has more than2keys, then search the rest. - If k is not found after traversing the whole tree, then the search element is not present in the
B Tree.
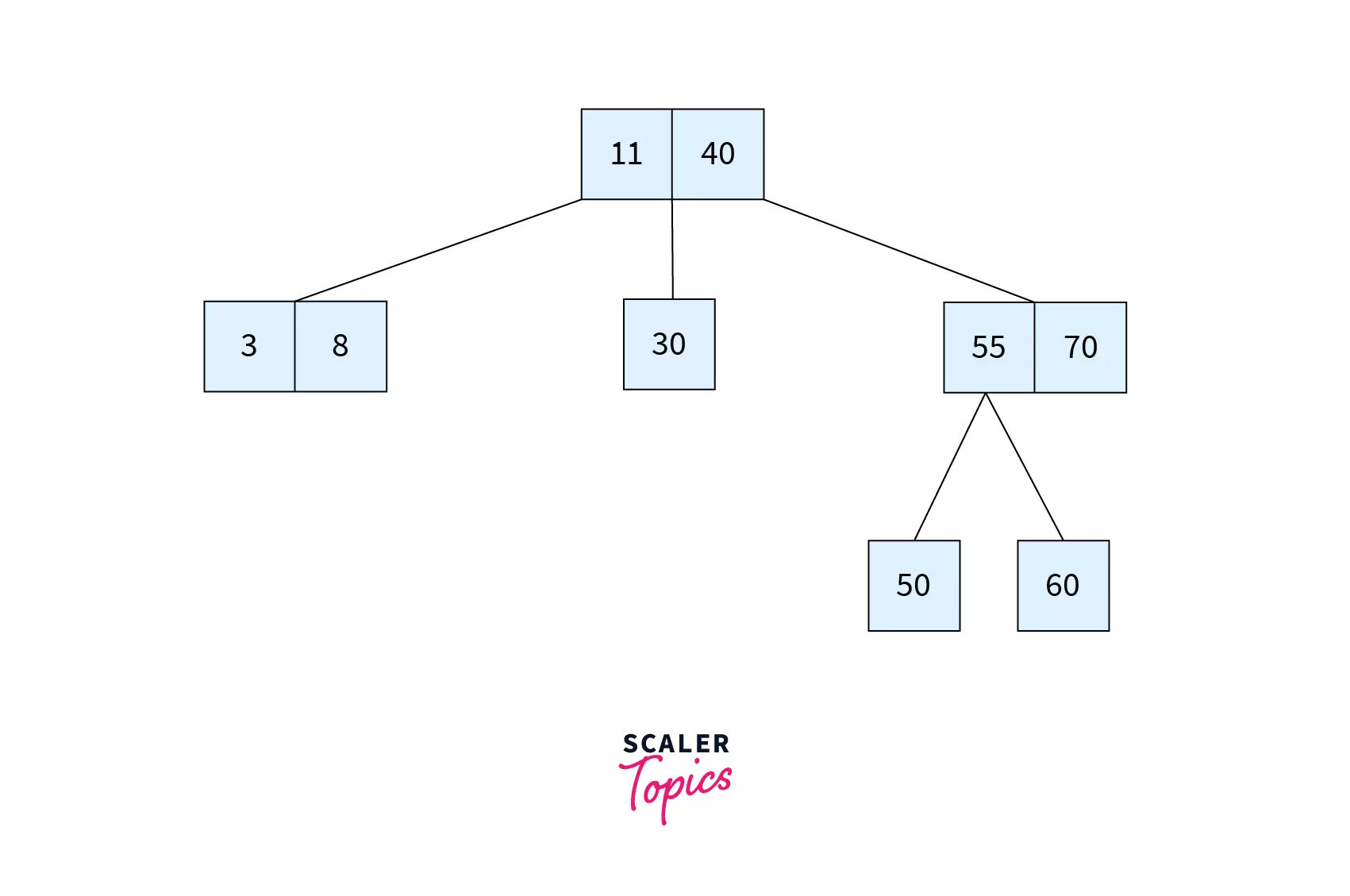
Let’s see this with the help of an example. Suppose that we want to search for a key k=32 in the B tree shown below.
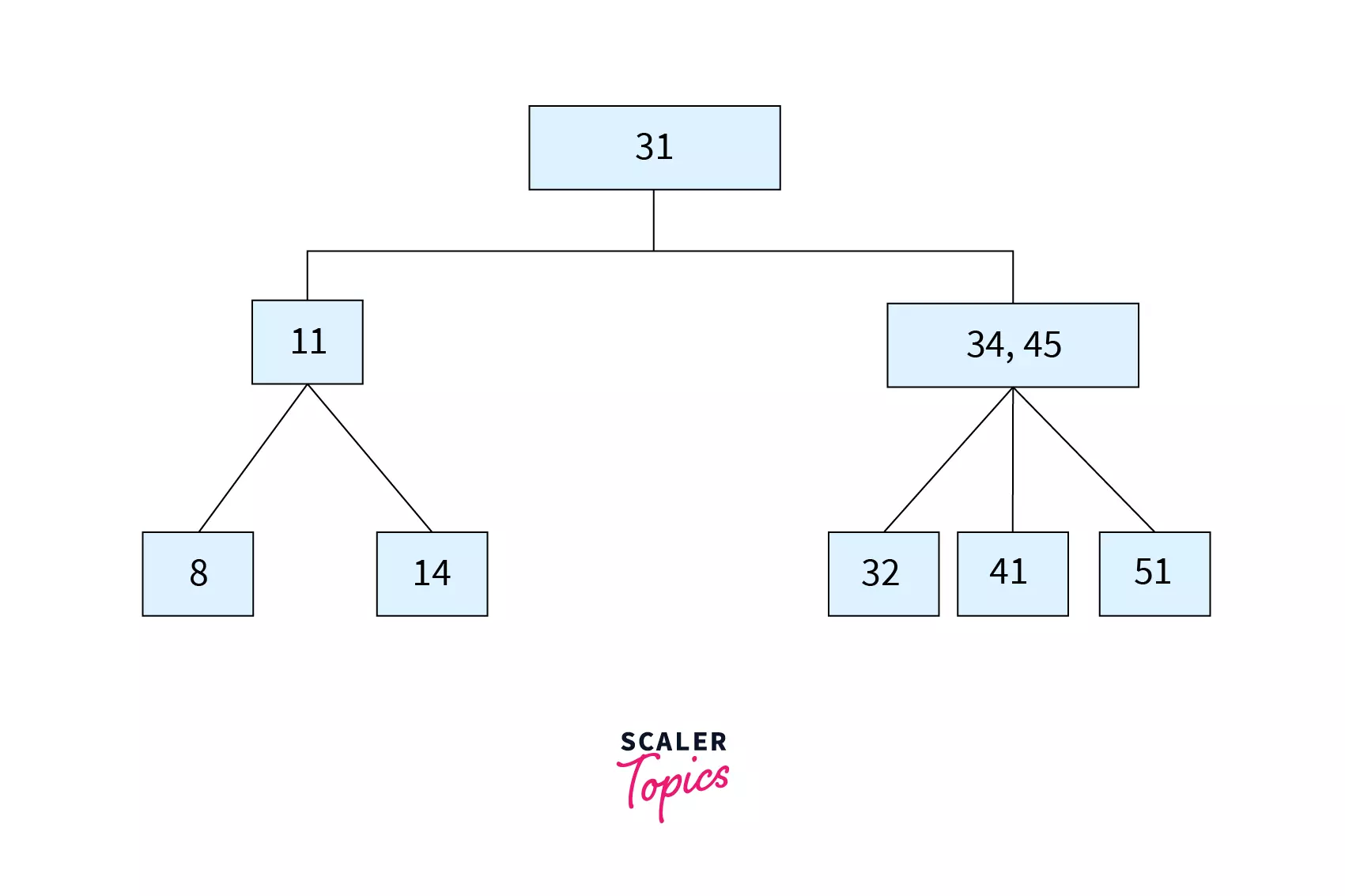
- We first check the root and realize that
k=32is not present here. So we move onto the children of the root node. Since it has 2 children here, we compare between the2 keys. - Since
k>31, go to the right child of the root node. - Compare
kwith the values of the node, i.e.34and45. Sincek<34(i.e. the left key), we move to the left child of34. - Since the value in left child of
34 = k = 32, we can say that the keykis found and search is complete.
In this particular example, we compared the key with 4 values until we found it. The time complexity required for the search operation in a B Tree is thus $O(log n)$.
Inserting Operation on B Tree in Data Structure
While inserting an element to B tree, we have to first check whether the element is already present in the tree. If the element is found, then the insertion doesn’t take place. If not, we will proceed further with the insertion. 2 cases need to be taken care of while inserting the key in the leaf node:
- Node does not contain more than
MAXnumber of keys – Simply insert the key in the node at its proper place. - Node contains
MAXnumber of keys – Key is inserted to the full node and then a split takes place splitting the full node into 3 parts. The second or median key moves to the parent node and the first and third parts act as the left and right children. The process is repeated with the parent node if it containsMAXnumber of keys too.
Steps to insert an element in B Tree in Data Structure
- Calculate the maximum number of keys in the node based on the order of the
B tree. - If the tree is empty, a root node is allocated and the key is inserted and acts as the root node.
- Search the appropriate node for insertion.`
- If the node is full:
4.1. Insert the elements in increasing order.
4.2. If the elements are greater than the maximum number of keys, split at the median.
4.3. Push the median key upwards and split the left and right keys as left and right child respectively. - If the node is not full, insert the node in increasing order.
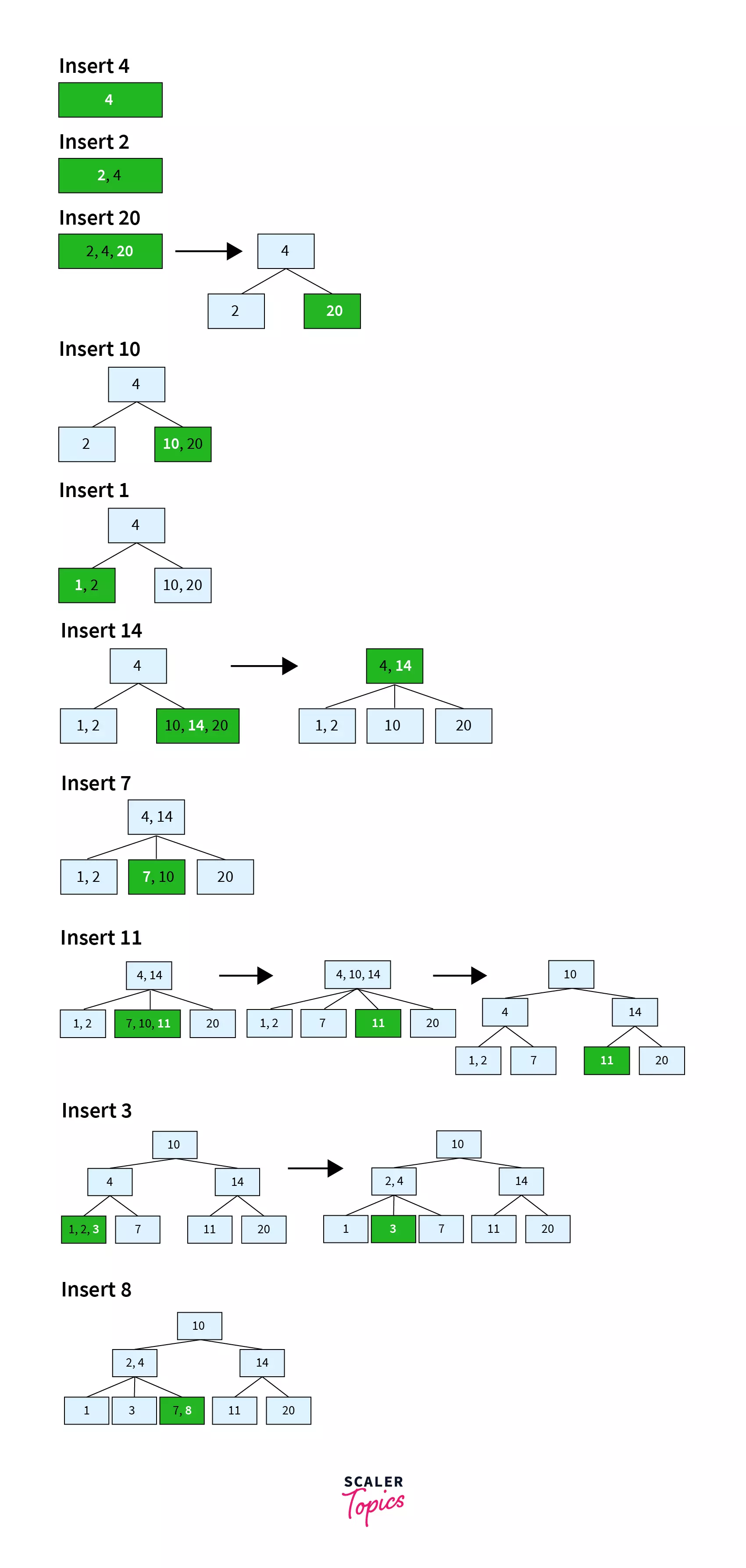
Suppose we have to create a B tree of order 4. The elements to be inserted are 4, 2, 20, 10, 1, 14, 7, 11, 3, 8.
Since m=3, max number of keys for a node = m-1 = 2.
- Insert
4 - Since
2<4, insert2to the left of4in the same node. - Since
20>4, insert20to the right of4in the same node. As we now, maximum number of keys in the node are2, one of these keys will have to be moved to a node above to split it. 4 being the middle element will move up and 2 and 20 will be its left and right nodes respectively. 10>4and10<20and thus,10will be inserted as a key in the node that contains 20 as a key.- Since
1<2, it will be inserted as a key in the node that contains2as a key. - 14>10 and
14<20. Since the number of keys in that node exceeds the maximum number of keys, the node will split after the middle key moves upto the node in the above line. Thus,14gets added to the right of4in the node that contains4, and10and20are split as2separate nodes. - Since
7<10, it gets inserted to the left in the node that contains10as a key. 11<14and11>10. Thus,11should get added to the right of the node that contains7and10. However, since the maximum number of keys in the tree are 2, a split should take place. Thus, the middle element10moves to the above node and7and11split as separate nodes. The above node now contains4, 10and14. Since the count of keys exceeds the maximum key count, there would be a split there. Now,10is the root node with4and14as its children.- Since
3<4and3>2,it gets inserted to the right of the node containing1, 2. This node exceeds the maximum count of keys in a node, leading to a split.2is added to the upper node beside 4. - Since
8>7and8<10, it gets added to the left of the node that contains7as a key.
In this particular example, the number of comparisons at each step varied. The first value was directly entered, thereafter every value had to be compared with the nodes present in the tree. The time complexity for insertion in a B Tree is dependent on the number of nodes and thus, O(log n).
The diagram below shows the insertions in order.
Deletion Operation on B Tree in Data Structure
During insertion, we had to ensure that the number of keys in the node doesn’t cross a maximum. Similarly, during deletion, we need to ensure that the number of keys in the node after deletion doesn’t go below the minimum number of keys that a node can hold. Thus, in case of deletion, a combination process takes place instead of a split.
Steps to delete an element in B Tree in Data Structure
Deletion can be studied using 2 cases:
- Deletion from a leaf node.
- Deletion from a non-leaf node.
The 2 cases can be represented by the following flowchart:
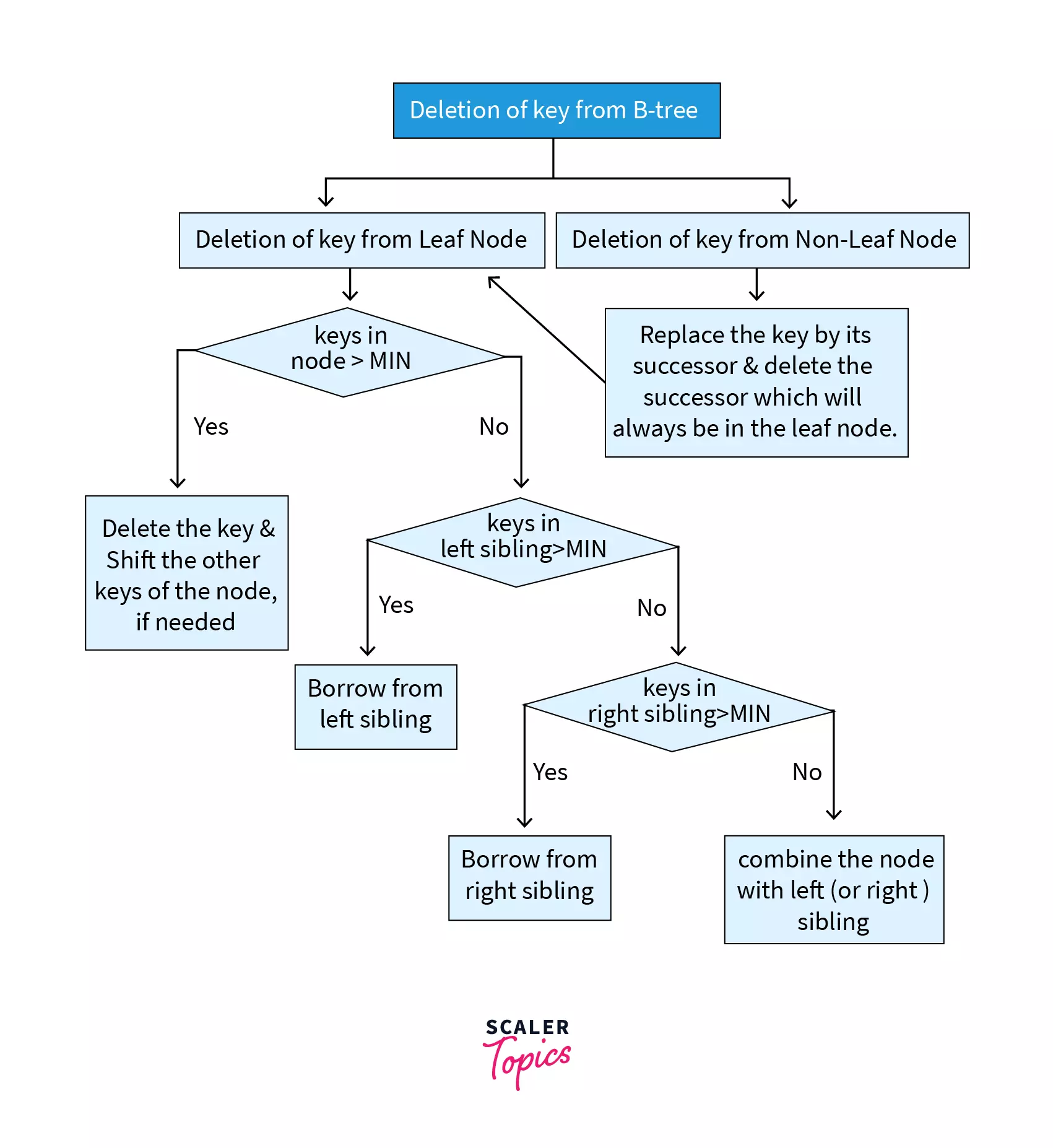
Case 1 – Deletion from Leaf Node
1.1. If the node has more than MIN keys – Deletion of key does not violate any property and thus the key can be deleted easily by shifting other keys of the node, if required.
1.2. If the node has less than MIN keys – This kind of deletion violates a property of B tree. In case the keys in the left sibling are greater than MIN, keys are borrowed from there. If the keys in right sibling are greater than MIN, then keys are borrowed from there. If either of these do not hold true, then a combination of node takes place with either of the siblings.
Case 2 – Deletion from Non-Leaf Node
In this case, the successor key (smallest key in the right subtree) is copied at the place of the key to be deleted and then the successor is deleted. This case further reduces to Case 1, i.e. deletion from a leaf node.
Now, let’s understand deletion using an example. Consider the following B tree of order 4 with the nodes 5, 12, 32 and 53 to be deleted in the given order.
Since the order of the B tree is 4, the minimum and maximum number of keys in a node are 2 and 4 respectively.
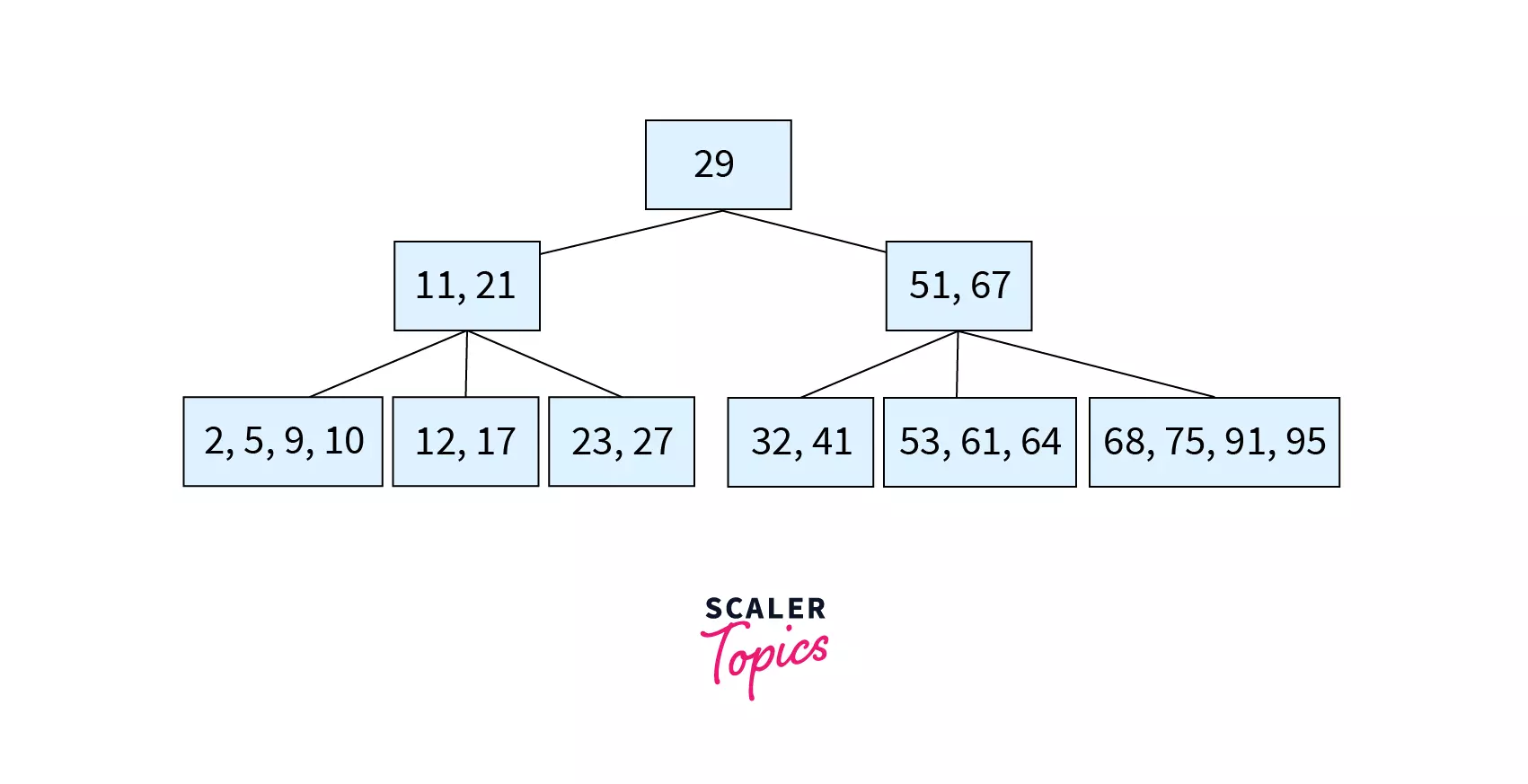
Step 1 – Deleting 5
Since 5 is a key in a leaf node with keys>MIN, this would be Case 1.1. A simple deletion with key shift would be done. Keys 9 and 10 are shifted left to fill the gap created by the deletion of 5.
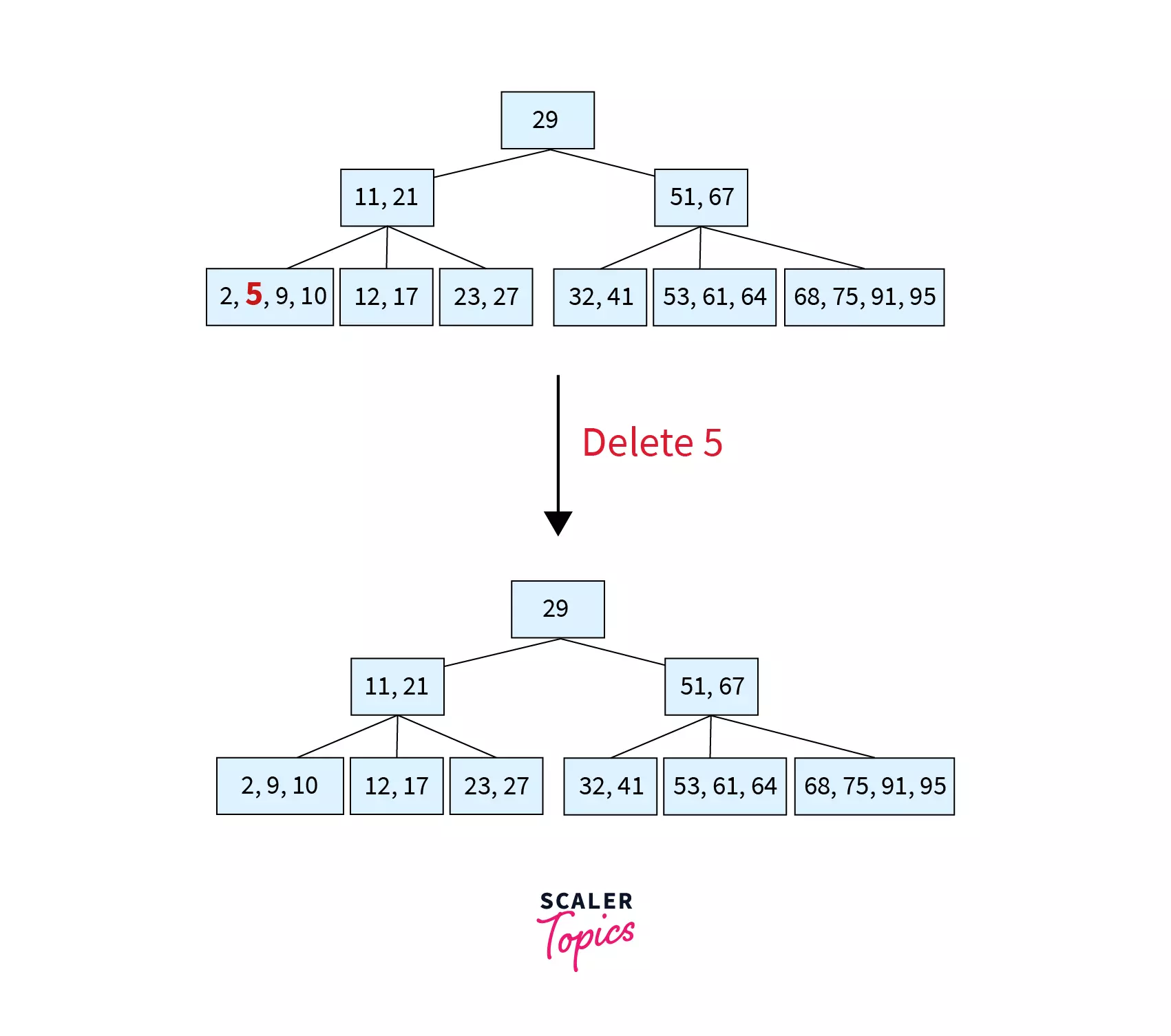
Step 2 – Deleting 12
Here, key 12 is to be deleted from node [12,17]. Since this node has only MIN keys, we will try to borrow from its left sibling [2,9,10] which has more than MIN keys. The parent of these nodes [11,21] contains the separator key 11. So, the last key of left sibling (10) is moved to the place of the separator key and the separator key is moved to the underflow node (the node where deletion took place). The resulting tree after deletion can be found as follows:
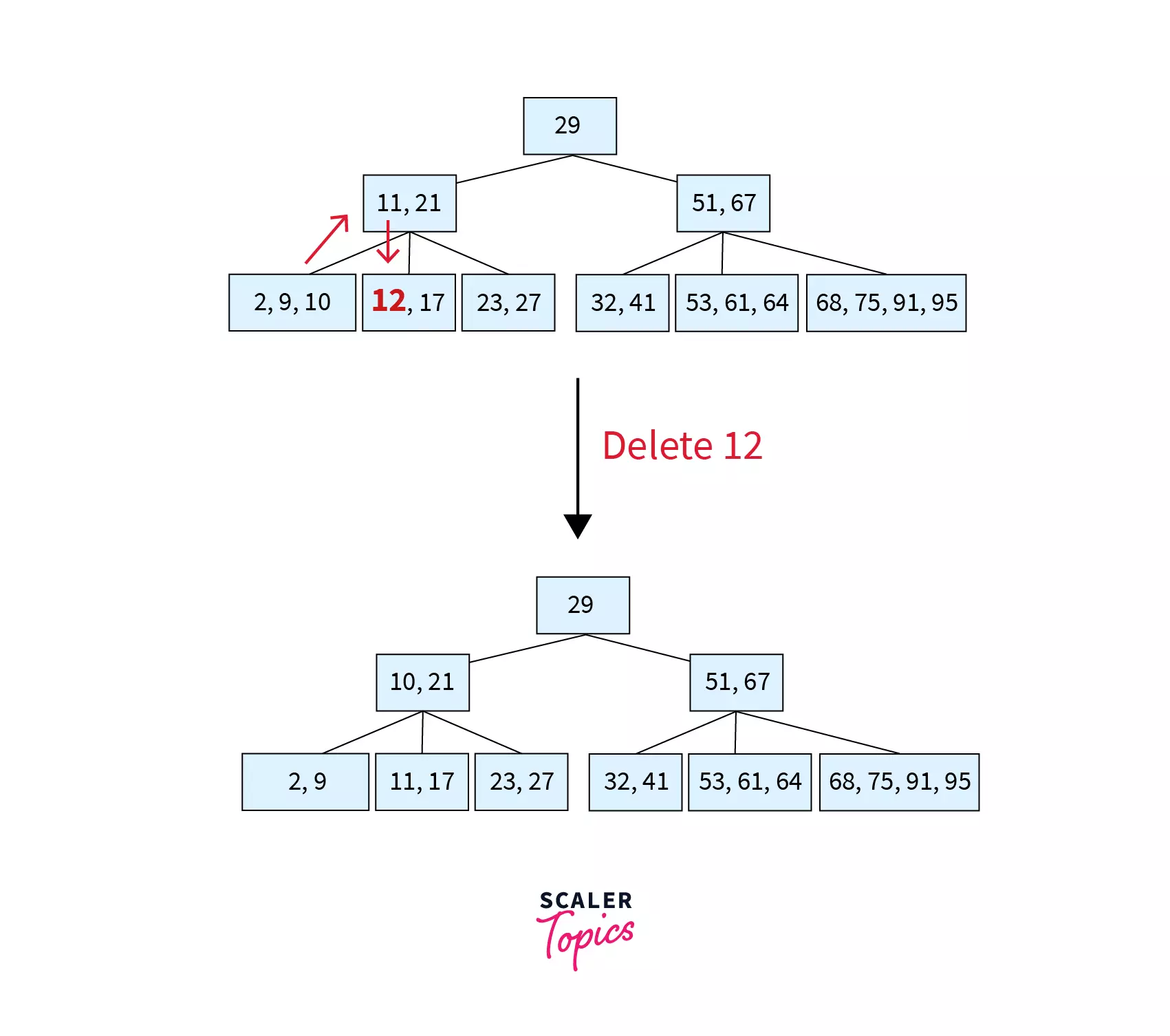
Step 3 – Deleting 32
Here, key 32 is to be deleted from node [32, 41]. Since this node has only MIN keys and does not have a left sibling, we will try to borrow from its right sibling [53, 61, 64] which has more than MIN keys. The parent of these nodes [51, 67] contains the separator key 51. So, the first key of right sibling (53) is moved to the place of the separator key and the separator key is moved to the underflow node (the node where deletion took place). The resulting tree after deletion can be found as follows:
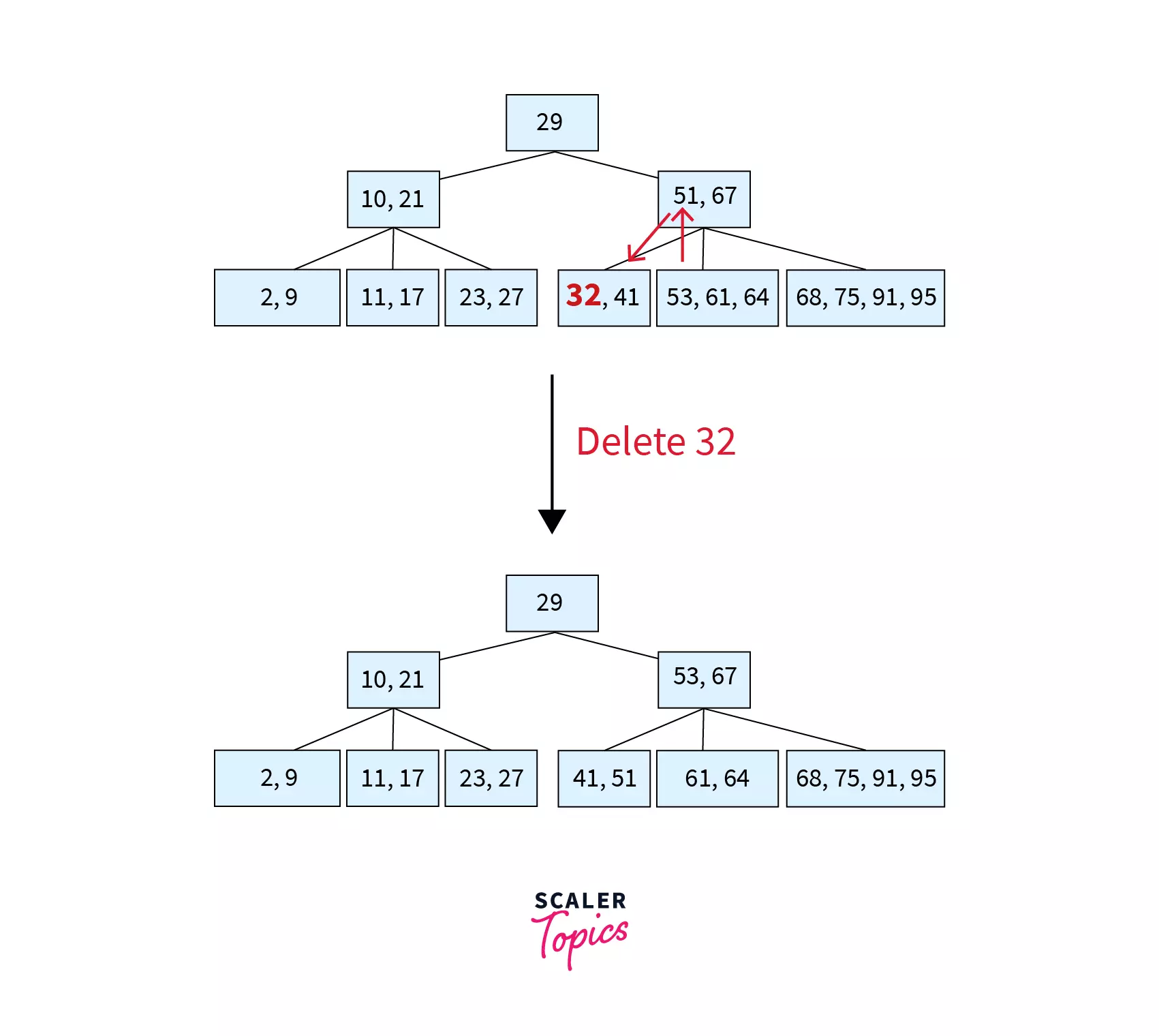
Step 4 – Deleting 53
Here key 53 is to be deleted from node [53, 67] which is a non-leaf node. In such a case, the successor key (61) will be copied in place of 53 and now the task reduces to deletion of 61 from the leaf node. Since this node would have less than MIN keys, we check for the left sibling. Since the left sibling has only MIN keys, we move to the right sibling. The leftmost key of the right sibling (68) moves to the parent node and replaces the separator (67) while the separator shifts to the underflow node making it [64,67]. The resulting tree after deletion can be found as follows:
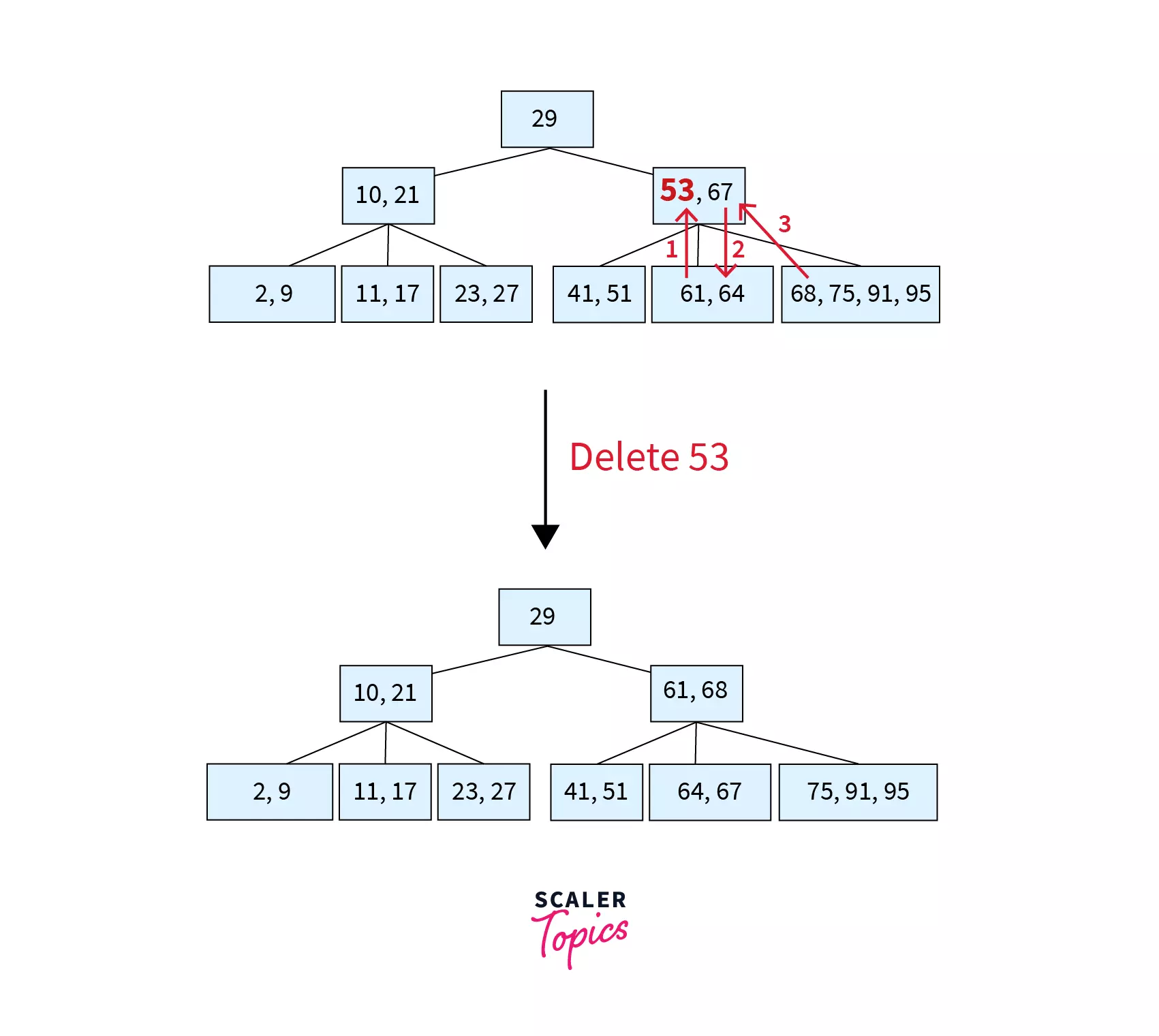
The time complexity here varies dependent on the location from where the key has to be deleted. The average time complexity required for the deletion operation in a B Tree is thus O(log n).
Application of B Tree
- Database or File System – Consider having to search details of a person in Yellow Pages (directory containing details of professionals). Such a system where you need to search a record among millions can be done using B Tree.
- Search Engines and Multilevel Indexing – B tree Searching is used in search engines and also querying in MySql Server.
- To store blocks of data – B Tree helps in faster storing blocks of data in secondary storage due to the balanced structure of B Tree.
B Tree Operation Code in Java / C++
Java
Creation of Node in B Tree
public class BNode {
int n;
int key[] = new int[2 * T - 1];
BNode child[] = new BNode[2 * T];
boolean leaf = true;
public int Find(int k) {
for (int i = 0; i < this.n; i++) {
if (this.key[i] == k) {
return i;
}
}
return -1;
};
}Search Operation in B Tree
private BNode Search(BNode x, int key) {
int i = 0;
if (x == null)
return x;
for (i = 0; i < x.n; i++) {
if (key < x.key[i]) {
break;
}
if (key == x.key[i]) {
return x;
}
}
if (x.leaf) {
return null;
} else {
return Search(x.child[i], key);
}
}Insertion Operation in B Tree
// Split function
private void Split(BNode x, int pos, BNode y) {
BNode z = new BNode();
z.leaf = y.leaf;
z.n = T - 1;
for (int j = 0; j < T - 1; j++) {
z.key[j] = y.key[j + T];
}
if (!y.leaf) {
for (int j = 0; j < T; j++) {
z.child[j] = y.child[j + T];
}
}
y.n = T - 1;
for (int j = x.n; j >= pos + 1; j--) {
x.child[j + 1] = x.child[j];
}
x.child[pos + 1] = z;
for (int j = x.n - 1; j >= pos; j--) {
x.key[j + 1] = x.key[j];
}
x.key[pos] = y.key[T - 1];
x.n = x.n + 1;
}
// Insert the key
public void Insert(final int key) {
BNode r = root;
if (r.n == 2 * T - 1) {
BNode s = new BNode();
root = s;
s.leaf = false;
s.n = 0;
s.child[0] = r;
Split(s, 0, r);
_Insert(s, key);
} else {
_Insert(r, key);
}
}
// Insert the Node
final private void _Insert(Node x, int k) {
if (x.leaf) {
int i = 0;
for (i = x.n - 1; i >= 0 && k < x.key[i]; i--) {
x.key[i + 1] = x.key[i];
}
x.key[i + 1] = k;
x.n = x.n + 1;
} else {
int i = 0;
for (i = x.n - 1; i >= 0 && k < x.key[i]; i--) {
}
;
i++;
BNode tmp = x.child[i];
if (tmp.n == 2 * T - 1) {
Split(x, i, tmp);
if (k > x.key[i]) {
i++;
}
}
_Insert(x.child[i], k);
}
}Deletion Operation in B Tree
private void delete_key(BNode x, int key) {
int pos = x.Find(key);
if (pos != -1) {
if (x.leaf) {
int i = 0;
for (i = 0; i < x.n && x.key[i] != key; i++) {
}
;
for (; i < x.n; i++) {
if (i != 2 * T - 2) {
x.key[i] = x.key[i + 1];
}
}
x.n--;
return;
}
if (!x.leaf) {
BNode pred = x.child[pos];
int predKey = 0;
if (pred.n >= T) {
for (;;) {
if (pred.leaf) {
System.out.println(pred.n);
predKey = pred.key[pred.n - 1];
break;
} else {
pred = pred.child[pred.n];
}
}
delete_key(pred, predKey);
x.key[pos] = predKey;
return;
}
BNode nextNode = x.child[pos + 1];
if (nextNode.n >= T) {
int nextKey = nextNode.key[0];
if (!nextNode.leaf) {
nextNode = nextNode.child[0];
for (;;) {
if (nextNode.leaf) {
nextKey = nextNode.key[nextNode.n - 1];
break;
} else {
nextNode = nextNode.child[nextNode.n];
}
}
}
delete_key(nextNode, nextKey);
x.key[pos] = nextKey;
return;
}
int temp = pred.n + 1;
pred.key[pred.n++] = x.key[pos];
for (int i = 0, j = pred.n; i < nextNode.n; i++) {
pred.key[j++] = nextNode.key[i];
pred.n++;
}
for (int i = 0; i < nextNode.n + 1; i++) {
pred.child[temp++] = nextNode.child[i];
}
x.child[pos] = pred;
for (int i = pos; i < x.n; i++) {
if (i != 2 * T - 2) {
x.key[i] = x.key[i + 1];
}
}
for (int i = pos + 1; i < x.n + 1; i++) {
if (i != 2 * T - 1) {
x.child[i] = x.child[i + 1];
}
}
x.n--;
if (x.n == 0) {
if (x == root) {
root = x.child[0];
}
x = x.child[0];
}
delete_key(pred, key);
return;
}
} else {
for (pos = 0; pos < x.n; pos++) {
if (x.key[pos] > key) {
break;
}
}
BNode tmp = x.child[pos];
if (tmp.n >= T) {
delete_key(tmp, key);
return;
}
if (true) {
BNode nb = null;
int devider = -1;
if (pos != x.n && x.child[pos + 1].n >= T) {
devider = x.key[pos];
nb = x.child[pos + 1];
x.key[pos] = nb.key[0];
tmp.key[tmp.n++] = devider;
tmp.child[tmp.n] = nb.child[0];
for (int i = 1; i < nb.n; i++) {
nb.key[i - 1] = nb.key[i];
}
for (int i = 1; i <= nb.n; i++) {
nb.child[i - 1] = nb.child[i];
}
nb.n--;
delete_key(tmp, key);
return;
} else if (pos != 0 && x.child[pos - 1].n >= T) {
devider = x.key[pos - 1];
nb = x.child[pos - 1];
x.key[pos - 1] = nb.key[nb.n - 1];
BNode child = nb.child[nb.n];
nb.n--;
for (int i = tmp.n; i > 0; i--) {
tmp.key[i] = tmp.key[i - 1];
}
tmp.key[0] = devider;
for (int i = tmp.n + 1; i > 0; i--) {
tmp.child[i] = tmp.child[i - 1];
}
tmp.child[0] = child;
tmp.n++;
delete_key(tmp, key);
return;
} else {
BNode lt = null;
BNode rt = null;
boolean last = false;
if (pos != x.n) {
devider = x.key[pos];
lt = x.child[pos];
rt = x.child[pos + 1];
} else {
devider = x.key[pos - 1];
rt = x.child[pos];
lt = x.child[pos - 1];
last = true;
pos--;
}
for (int i = pos; i < x.n - 1; i++) {
x.key[i] = x.key[i + 1];
}
for (int i = pos + 1; i < x.n; i++) {
x.child[i] = x.child[i + 1];
}
x.n--;
lt.key[lt.n++] = devider;
for (int i = 0, j = lt.n; i < rt.n + 1; i++, j++) {
if (i < rt.n) {
lt.key[j] = rt.key[i];
}
lt.child[j] = rt.child[i];
}
lt.n += rt.n;
if (x.n == 0) {
if (x == root) {
root = x.child[0];
}
x = x.child[0];
}
delete_key(lt, key);
return;
}
}
}
}
public void delete_key(int key) {
BNode x = Search(root, key);
if (x == null) {
return;
}
delete_key(root, key);
}Display B Tree
// display the node
private void display(Node x) {
assert (x == null);
for (int i = 0; i < x.n; i++) {
System.out.print(x.key[i] + " ");
}
if (!x.leaf) {
for (int i = 0; i < x.n + 1; i++) {
display(x.child[i]);
}
}
}
public void display() {
display(root);
}C++
Creation of Node in B Tree
class BNode {
int *keys;
int t;
BNode **C;
int n;
bool leaf;
public:
BNode(int _t, bool _leaf);
void display();
int findKey(int k);
void insertNonFull(int k);
void splitChild(int i, BNode *y);
void delete_key(int k);
void removeFromLeaf(int idx);
void removeFromNonLeaf(int idx);
int getPredecessor(int idx);
int getSuccessor(int idx);
void fill(int idx);
void borrowFromPrev(int idx);
void borrowFromNext(int idx);
void merge(int idx);
friend class BTree;
};
class BTree {
BNode *root;
int t;
public:
BTree(int _t) {
root = NULL;
t = _t;
}
BNode *search(int k) {
return (root == NULL) ? NULL : root->search(k);
}
void insert_key(int k);
};Search Operation in B Tree
int BNode::search_key(int k) {
int idx = 0;
while (idx < n && keys[idx] < k)
++idx;
return idx;
}Insertion Operation in B Tree
// Insertion operation
void BTree::insert_key(int k) {
if (root == NULL) {
root = new BNode(t, true);
root->keys[0] = k;
root->n = 1;
} else {
if (root->n == 2 * t - 1) {
BNode *s = new BNode(t, false);
s->C[0] = root;
s->splitChild(0, root);
int i = 0;
if (s->keys[0] < k)
i++;
s->C[i]->insertNonFull(k);
root = s;
} else
root->insertNonFull(k);
}
}
// Insertion non full
void BNode::insertNonFull(int k) {
int i = n - 1;
if (leaf == true) {
while (i >= 0 && keys[i] > k) {
keys[i + 1] = keys[i];
i--;
}
keys[i + 1] = k;
n = n + 1;
} else {
while (i >= 0 && keys[i] > k)
i--;
if (C[i + 1]->n == 2 * t - 1) {
splitChild(i + 1, C[i + 1]);
if (keys[i + 1] < k)
i++;
}
C[i + 1]->insertNonFull(k);
}
}
// Split child
void BNode::splitChild(int i, BNode *y) {
BNode *z = new BNode(y->t, y->leaf);
z->n = t - 1;
for (int j = 0; j < t - 1; j++)
z->keys[j] = y->keys[j + t];
if (y->leaf == false) {
for (int j = 0; j < t; j++)
z->C[j] = y->C[j + t];
}
y->n = t - 1;
for (int j = n; j >= i + 1; j--)
C[j + 1] = C[j];
C[i + 1] = z;
for (int j = n - 1; j >= i; j--)
keys[j + 1] = keys[j];
keys[i] = y->keys[t - 1];
n = n + 1;
}Deletion Operation in B Tree
// Deletion operation
void BNode::delete_key(int k) {
int idx = findKey(k);
if (idx < n && keys[idx] == k) {
if (leaf)
removeFromLeaf(idx);
else
removeFromNonLeaf(idx);
} else {
if (leaf) {
cout << "The key " << k << " is does not exist in the tree\n";
return;
}
bool flag = ((idx == n) ? true : false);
if (C[idx]->n < t)
fill(idx);
if (flag && idx > n)
C[idx - 1]->delete_key(k);
else
C[idx]->delete_key(k);
}
return;
}
// Remove from the leaf
void BNode::removeFromLeaf(int idx) {
for (int i = idx + 1; i < n; ++i)
keys[i - 1] = keys[i];
n--;
return;
}
// Delete from non leaf node
void BNode::removeFromNonLeaf(int idx) {
int k = keys[idx];
if (C[idx]->n >= t) {
int pred = getPredecessor(idx);
keys[idx] = pred;
C[idx]->delete_key(pred);
}
else if (C[idx + 1]->n >= t) {
int succ = getSuccessor(idx);
keys[idx] = succ;
C[idx + 1]->delete_key(succ);
}
else {
merge(idx);
C[idx]->delete_key(k);
}
return;
}
int BNode::getPredecessor(int idx) {
BNode *cur = C[idx];
while (!cur->leaf)
cur = cur->C[cur->n];
return cur->keys[cur->n - 1];
}
int BNode::getSuccessor(int idx) {
BNode *cur = C[idx + 1];
while (!cur->leaf)
cur = cur->C[0];
return cur->keys[0];
}
void BNode::fill(int idx) {
if (idx != 0 && C[idx - 1]->n >= t)
borrowFromPrev(idx);
else if (idx != n && C[idx + 1]->n >= t)
borrowFromNext(idx);
else {
if (idx != n)
merge(idx);
else
merge(idx - 1);
}
return;
}
// Borrow from previous
void BNode::borrowFromPrev(int idx) {
BNode *child = C[idx];
BNode *sibling = C[idx - 1];
for (int i = child->n - 1; i >= 0; --i)
child->keys[i + 1] = child->keys[i];
if (!child->leaf) {
for (int i = child->n; i >= 0; --i)
child->C[i + 1] = child->C[i];
}
child->keys[0] = keys[idx - 1];
if (!child->leaf)
child->C[0] = sibling->C[sibling->n];
keys[idx - 1] = sibling->keys[sibling->n - 1];
child->n += 1;
sibling->n -= 1;
return;
}
// Borrow from the next
void BNode::borrowFromNext(int idx) {
BNode *child = C[idx];
BNode *sibling = C[idx + 1];
child->keys[(child->n)] = keys[idx];
if (!(child->leaf))
child->C[(child->n) + 1] = sibling->C[0];
keys[idx] = sibling->keys[0];
for (int i = 1; i < sibling->n; ++i)
sibling->keys[i - 1] = sibling->keys[i];
if (!sibling->leaf) {
for (int i = 1; i <= sibling->n; ++i)
sibling->C[i - 1] = sibling->C[i];
}
child->n += 1;
sibling->n -= 1;
return;
}
// Merge
void BNode::merge(int idx) {
BNode *child = C[idx];
BNode *sibling = C[idx + 1];
child->keys[t - 1] = keys[idx];
for (int i = 0; i < sibling->n; ++i)
child->keys[i + t] = sibling->keys[i];
if (!child->leaf) {
for (int i = 0; i <= sibling->n; ++i)
child->C[i + t] = sibling->C[i];
}
for (int i = idx + 1; i < n; ++i)
keys[i - 1] = keys[i];
for (int i = idx + 2; i <= n; ++i)
C[i - 1] = C[i];
child->n += sibling->n + 1;
n--;
delete (sibling);
return;
}
void BTree::delete_key(int k) {
if (!root) {
cout << "The tree is empty\n";
return;
}
root->delete_key(k);
if (root->n == 0) {
BNode *tmp = root;
if (root->leaf)
root = NULL;
else
root = root->C[0];
delete tmp;
}
return;
}Display Tree in B Tree
void display() {
if (root != NULL)
root->display();
}Time Complexity of B Tree
In a B tree, disk access times are much lower than other trees like AVL Tree, Red-Black Tree, etc. due to its low height. If we consider n to be the total number of elements in a B tree, the best case time complexity for any of the common operations, i.e. Search, insert and delete will be O(log n).
Unlock the Power of Efficient Coding! Join Our DSA Course Today and Transform Your Problem-Solving Abilities.
Summary
- The
B Treeis a data structure that aids in data operations such as insertion, deletion, and traversal. - Disk access times in
B treesare much lower due to the low height of these trees. B treesare extremely useful in real-world scenarios requiring large datasets due to its balanced structure.