A Stack is a linear data structure that processes elements in a last in first out (LIFO) manner, with the most recent element always on top. Push() and pop() operations are usually supported. Applications of stack in data structure includes expression evaluation, backtracking, recursion and the implementation of other data structures such as queues.
Applications of Stack in Data Structure
We’ve included several frequent yet important real-world applications of stack data in structure.
1. Expression Handling
Stack data structures are highly effective in evaluating arithmetic operations, basically, it evaluates the expression by converting it into a specific notation (prefix or postfix) and then calculate its values.
There are three common notations for expressing an arithmetic expression.
- Infix Notation Each operator is placed between the operands in the infix notation, which is a convenient manner of constructing an expression. Depending on the situation, infix expressions may or may not be parenthesized. (A+B)+C*(E-F) is an example of Infix Notation
- Prefix Notation The operator is placed before the operands in the prefix notation. This system was created by a Polish mathematician, and is thus known as polish notation. + A B and *+ABC are the examples of Polish notation Where *+ABC = (A+B)*C in infix notation
- Postfix Notation The operator is placed after the operands in postfix notation. This notation is known as Reverse Polish notation since it is the inverse of Polish notation. AB + // example
The key purpose now is to evaluate these expressions using the stack data structure. Consider the following scenario: we’ve been given the postfix notation of an expression, and we’ll use the stack data structure to determine its value.
Expression A = 1 2 3 4 + * * 28 / 1 –
Answer : -1
The idea is to push each element into the stack one by one untill we encunter any algebric operator(+,-1,*,/), then pop two elements and perform the operation over them and push the result back into the stack.
| Character | Operation | Stack |
|---|---|---|
| 1 | Push 1 into stack | 1 |
| 2 | Push 2 into stack | 2 1 |
| 3 | Push 3 into stack | 3 2 1 |
| 4 | Push 4 into stack | 4 3 2 1 |
| + | pop two elements (4,3) and do 4+3 and push the result back into stack | 7 2 1 |
| * | pop 7 and 2 do (7*2) and push the result back | 14 1 |
| * | pop 14 and 1 from the stack and push 14*1 into stack | 14 |
| 28 | push 28 into stack | 28 14 |
| / | Pop 28 and 14 from the stack and do 28/14=2 and push 2 into stack | 2 |
| 1 | Push 1 into stack | 1 2 |
| – | Pop 1 and 2 from and do 1-2 and push -1 into the stack | -1 |
Now, we have processed all the elements and the only remaing digit in the stack -1 is our answer.
2. Backtracking
One of the algorithm design techniques is backtracking. For that aim, we dig into one path; if that path is inefficient, we return to the previous state and explore alternative options. We must save the previous state in order to return from the current state. Stack is required for this purpose. A famous example is N-queens problems.
3. Reverse a Data
We already know that the data is processed in a LIFO (last in, first out) way by the stack i.e. last element will automatically be returned first, hence resulting the reversed data.
Cosider a string s = “Apple” and we want to reverse it. The approach would be to push all the elements from the begining of the string and pop out then, as the last entered element will be the first to come out of the stack, and same is followed for the rest of the elements, resulting the reversed string “elppA”.
4. Parenthesis Checking
One of the most common uses of the stack is to see if the provided expression’s parentheses are balanced.
Stack is one way to check for balanced parenthesis. When you come across an open parentheses, put it into the stack, and when you come across a closed parenthesis, match it to the top of the stack and pop it, if the stack is empty return unbalanced. Return balanced if the stack is empty at the end, unbalanced Otherwise.
5. Processing Function Calls
We often see terms like call stack and recursion stack often being used in programming. Whenever a function(A) calls another function(B), the address of caller function is stored and when the call of function B is finished, the computation for function A is performed and address of A is removed from the stack and the apporiprate output is returned. Consider the example of two functions A() and B(), the function A() calls B() first and then prints a statement, on the other hand, B() only prints a single statement and terminates the call from there.
// function B
B(){
print("call for B is finished");
}
// function A
A(){
B();
print("Call for A is finished");
}
- Firstly the control in function A(), therefore function A() is called and its address adrA is stored into the call stack.
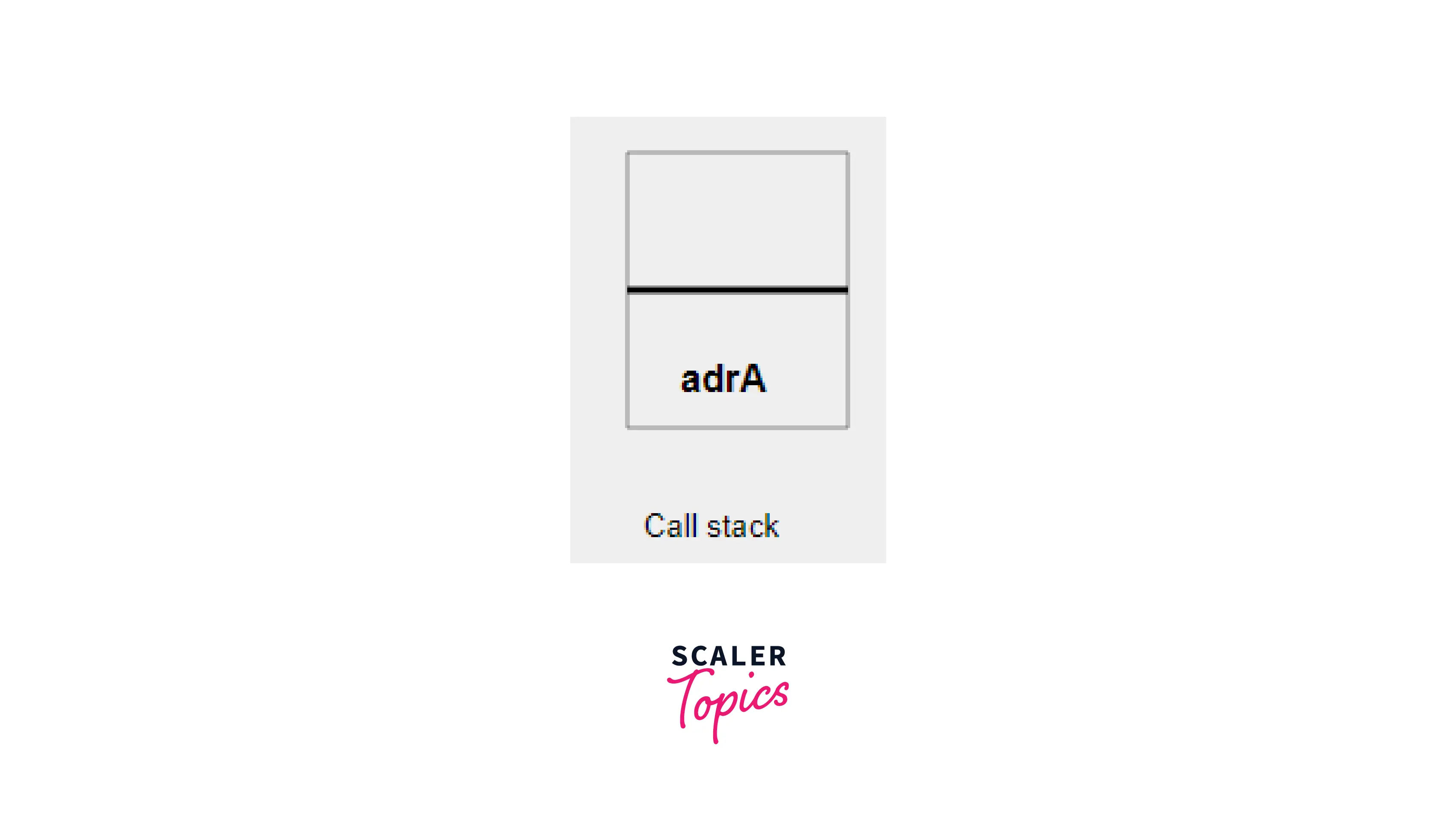
- Now the first line in the body of A() executes and function B() is called, and the address of B(), adrB is stored in the call stack.
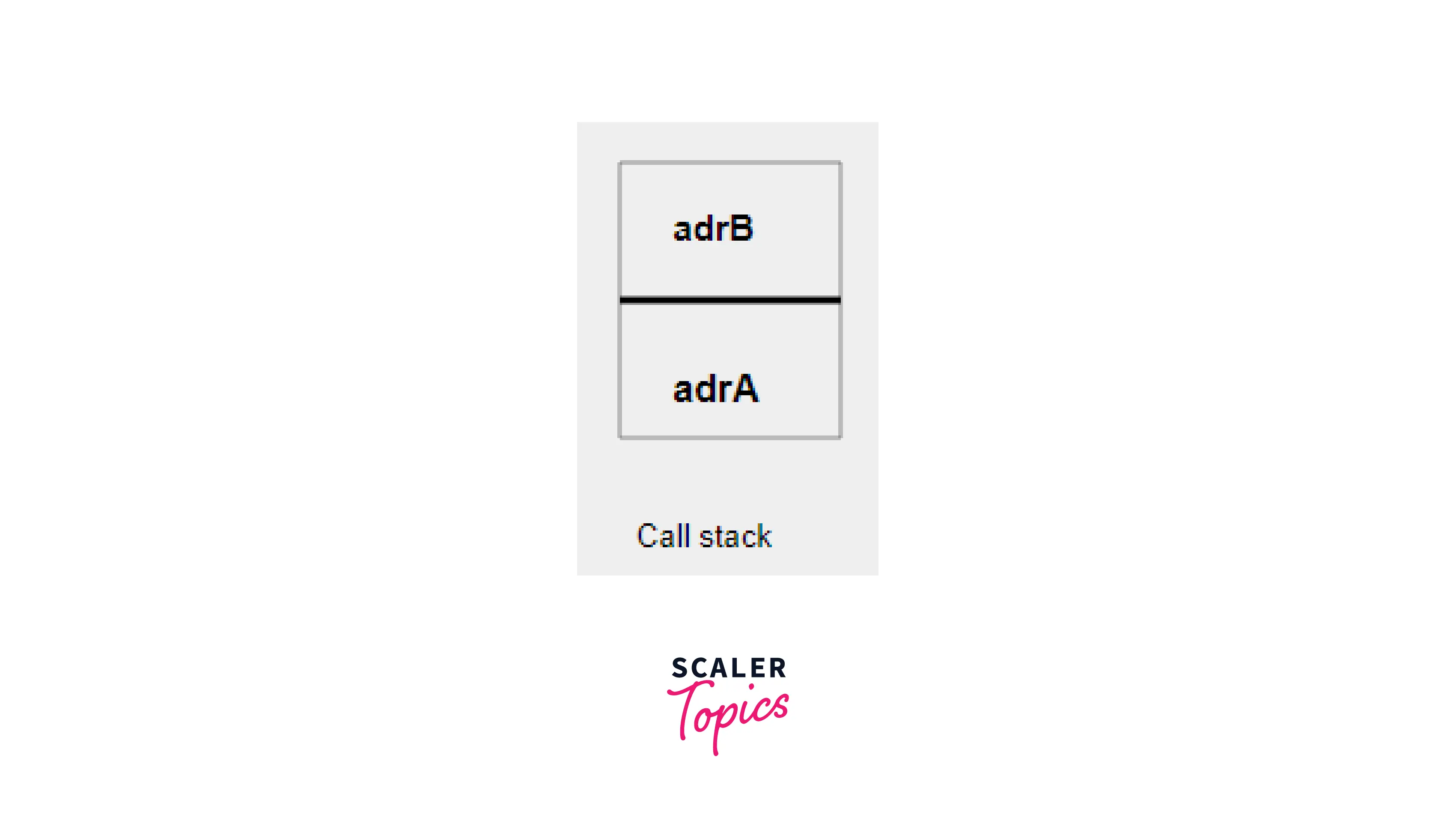
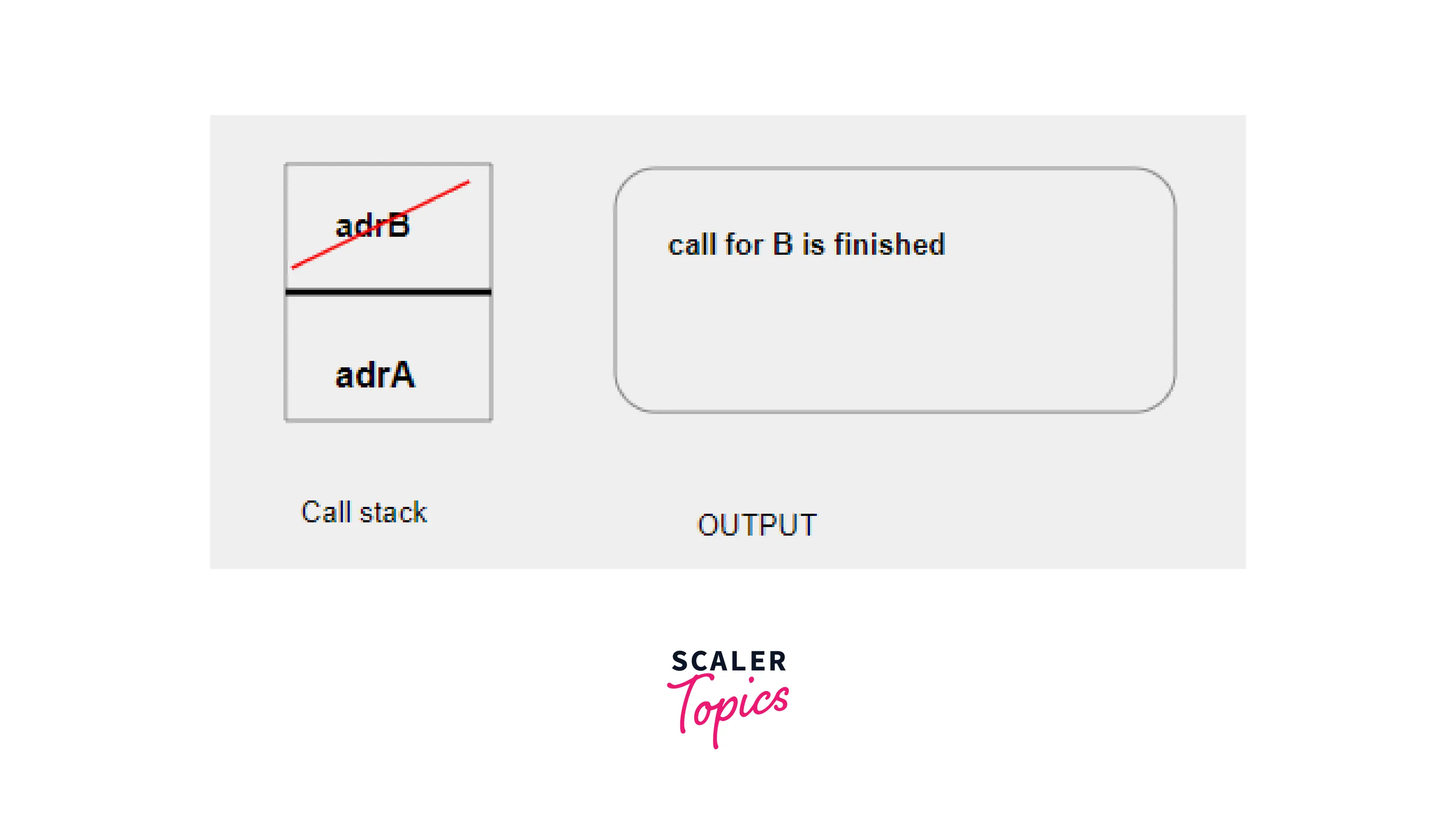
- Now the first line in the body of B() executes and that prints the statement, since there are no more lines in B() to execute so its call is over, its address is popped out of the stack and control comes back to function A().

- Now A() executes its second line and prints the given statement, now A’s call is over so its address also popped out and the program terminates.
6. Queue using Stacks
Implementing a queue data structure with stack is a well-known challenge solved with stack. The idea is to implement queue data structure which supports push() ,pop() and front() using stack.
This problems can be solved using two stacks s1, and s2. In this method, we simply call the push() function to add a new element to the stack s1, however doing so will push our first element to the bottom of the stack as we add more elements to the stack. However, we want to remove the first element first in the dequeue procedure. As a result, we’ll have to use the second stack s2.
Following steps can be followed for better implementation:
- push every input element into stack one.
- If dequeue() is called:
- If s2 is empty:
- If s1 is empty:
- The queue is empty and dequeue can not be performed.
- Else:
- Pop all the elements from s1 and push them into s2 and return top() of s2 and pop() one element from s2.
- If s1 is empty:
- Else:
- return top of s2 and pop one element from s2.
- If s2 is empty:
Supercharge Your Coding Skills! Enroll Now in Our DSA Course and Master Algorithmic Excellence.
Conclusion
- Stack is useful for tasks like expression evaluation, parenthesis balance, and the N-Queens problem.
- This can also be used to implement other data structures such as queues.