An algorithm is a step-by-step set of instructions, which are meaningful and used to solve any particular problem. To perform every process, there is a set of Algorithms, which lets us know how to proceed with the problem and solve it in some steps.
The analysis of an algorithm is a technique that measures the performance of an algorithm. The factors over which the algorithms majorly depend are the space and time complexities. There are other factors as well, which we use for the analysis of algorithms, we will learn about them ahead in the article.
Takeaways
Analysis of algorithms is the process of finding the computational complexity of any algorithm.
Introduction to Algorithms
Algorithms are step-by-step instructions that help us in doing some tasks. For example, if you want to cook maggie(let’s suppose), then you will be following the below algorithm :
- Boil some water in a Pan
- Add maggie into it
- Add maggie masala
- Check for toppings
- If present :
- Sprinkle them
- Else :
- Do not sprinkle
- If present :
- Serve the maggie
Similarly, in the computer science terminologies, an algorithm is defined as the set of well-defined instructions, that helps us to solve any particular problem.

For example, the algorithm to add two numbers will be :
- Take two numbers as input
- Perform arithmetic addition using (‘+’) operator
- Return the result
There are certain parameters that we should note while writing any algorithm.
The parameters for good algorithms are stated below :
- The input and output of the algorithm must be accurate.
- The steps in the algorithm should be clear and with no ambiguity
- It should be effective, to solve a problem.
- The algorithm should not be written in any programming language. That means, it should be possible for the users to code the algorithm into any of the programming languages of their choice.
What is the Analysis of the Algorithm ?
Analysis of algorithms is the process of finding the computational complexity of any algorithm. By computational complexity, we are referring to the amount of time taken, space, and any other resources needed to execute(run) the algorithm.
The goal of algorithm analysis is to compare different algorithms that are used to solve the same problem. This is done to evaluate which method solves a certain problem more quickly, efficiently, and memory-wise.

Usually, the time complexity is determined by the size of the algorithm’s input to the number of steps taken to execute it. Also, the space complexity is mostly determined by the amount of storage needed by the algorithm to execute.
If an algorithm runs in a reasonable amount of time or space on any machine, where that time and space are measured as a function of the size of the input (usually), then the algorithm is considered to be efficient. In simple terms, if the resource consumption or the computation cost of an algorithm grows slowly with the growth of the size of the input, then the algorithm might be considered as efficient. Do not worry if these terms confuse you, we will be learning about these in great depth ahead in the article.
What is the Need for Analysis of the Algorithm ?
Let’s say you created a website where users may read and post blogs. In the early stages of development, the website’s user base is quite small (say 10−2010−20 users). But with time, the number of users on your website grows dramatically, reaching 40k – 50k users. Now, the questions that will start popping into your mind are :
- Will my website scale well with these many users ?
- Or, it would start lagging and take a great time to respond to any user ?
So, these issues would not arise if you had addressed them when designing your website. But, if you neglected these factors in the beginning, then there are higher chances that your code will crash for indefinitely large inputs.
Hence, here the analysis of algorithms comes into the picture! Let us now see why is the analysis of the algorithm so important :
- By analyzing an algorithm, we get an idea of how the algorithm will scale with the variation (change) in the input size.
- Another reason for analysis of the algorithm is to compare various algorithms for solving the same problem. Through this, we can determine which algorithm will suit best the problem. Suppose, we have 2 algorithms for a single problem, one that takes O(N2) and another that takes O(N). Then we can say that the algorithm with a time complexity of O(N) will perform much better than the one with O(N2).
- Analysis of the algorithms also helps us in understanding the space that will be taken by our code.
What are Asymptotic Notations ?
Asymptotic notations in general tell us about how good an algorithm performs when compared to another algorithm.
However, we cannot simply compare two algorithms directly. To compare two algorithms, factors such as the hardware and the tools we are using also have a remarkable impact. For example, the performance of algorithms varies with variations in the operating systems, the processors, etc. So, even though we’ve calculated the performance of two algorithms on a particular system, there are chances that they will perform differently on different systems.
To tackle the above-stated issues, we use the asymptotic analysis to compare the space and time complexity of the algorithms. The asymptotic analysis analyzes two algorithms based on their performance when the input size is varied (increased or decreased).
There are three types of Asymptotic notations. They are as stated below :

- Big-Oh (O) notation.
- Big Omega (Ω) notation.
- Big Theta (Θ) notation.
The above notations are used to measure the worst, best, and average time complexities of the algorithms. In the next point, we will understand them in detail.
Types of Algorithm Analysis
Till now we must already be aware that, the running time of an algorithm increases with the increase in the size of the input. However, if the running time is constant then it will remain constant, no matter what the input is.
Even if the size of the input is the same sometimes, the running time of the algorithm still may vary. Hence, we perform the best, average, and worst-case analyses of the algorithms, covering all the possible cases where the algorithm may behave abruptly high or low.
There are four types of analysis of algorithms. They are stated below :
- Best case
- Average case
- Worst case
- Amortized analysis
Let us look at each of them in detail.
1. Best Case Analysis of Algorithms
The best case analysis of algorithms gives us the lower bound on the running time of the algorithm for any given input. In simple words, it states that any program will need at least (greater than or equal to) that time to run. For example, suppose we have an algorithm that has the best case time complexity is O(N), then we can say that the program will take a minimum of O(N) time to run, it can never take sometime less than that.
The best case time or space complexity is often represented in terms of the Big Omega (Ω) notation.
Example for Best Case Analysis :
Let us take the example of the linear search to calculate the best time complexity. Suppose, you have an array of numbers and you have to search for a number.
Find the code below for the above problem :
Code :
int linear_search(int arr, int l, int target) {
int i;
for (i = 0; i < l; i++) {
if (arr[i] == target) {
return arr[i]
}
}
return -1
}
Now suppose, the number you are searching for is present at the very beginning index of the array. In that case, your algorithm will take O(1) time to find the number in the best case. So, the best case complexity for this algorithm becomes O(1), and you will get your output in a constant time.
How frequently do we use the best case analysis of any algorithm ?
The best case is rarely necessary for measuring the runtime of the algorithms in practice. An algorithm is never created using the best-case scenario.
2. Worst Case Analysis of Algorithms
The worst-case analysis of algorithms gives us the upper bound on the running time of the algorithm for any given input. In simple words, it states that any program will need maximum that time (less than or equal to) to run. For example, suppose we have an algorithm that has the worst-case time complexity is O(N2), then we can say that the program will take a maximum of O(N2) time to run, for an input of size N it can never take more time than that to run.
The worst-case time or space complexity is often represented in terms of the Big Oh (O) notation.
Example for worst case analysis :
Let us take our previous example where we were performing the linear search. Suppose, this time the element we are trying to find is at the end of the array. So, we will have to traverse the whole array before finding the element. Hence, we can say that the worst case for this algorithm is O(N) itself. Because we have to go through at most N elements before finding our target. So, this is how we calculate the worst case of the algorithms.
How frequently do we use the worst-case analysis of any algorithm?
In actual life, we typically analyze an algorithm’s worst-case scenario for most of the cases. The longest running time W(n) of an algorithm for any input of size n is referred to as worst-case time complexity.
3. Average Case Analysis of Algorithms
As the name suggests, the average case analysis of algorithms takes the sum of the running time on every possible input, and after that, it takes the average. So, in this case, the execution time of the algorithm acts as both the lower and upper bound. In simple terms, we can get an idea of the average running time of the algorithm through it.
Generally, the average case of the algorithms is as high as the worst-case running of it. Hence, it roughly gives us an estimation of the worst case itself.
The average case time or space complexity is often represented in terms of the Big theta (Θ) notation.
Example for average case analysis :
In our previous example, suppose we need to find any element which is present in the mid of our array. So, for that, we need to traverse at least the half length of the array. In other words, it will take us O(n/2) time for us to traverse the half-length. The time complexity O(n/2) is as good as O(n). That is why we say that the average case in most of the cases depicts the worst case of an algorithm.
How frequently do we use the average case analysis of any algorithm ?
To be precise, it is usually difficult to analyze the average case running time of an algorithm. It is simpler to calculate the worst case instead. This is mainly because it might not be a very exact thing to declare any input as the “average” input for any problem. Therefore, prior knowledge of the distribution of the input cases is necessary for a useful examination of the average behavior of an algorithm, which is necessarily an impossible condition.
4. Amortized Analysis of Algorithms
The amortized analysis of the algorithms mainly deals with the overall cost of the operations. It does not mention the complexity of any one particular operation in the sequence. The total cost of the operations is the major focus of amortized analysis.
In times when only a few operations are slow but a majority of other operations are quicker, we perform an amortized analysis. Through this, we return the average running time per operation in the worst case.
Example for Amortized case analysis
A perfect example of understanding the amortized case analysis would be a hash table. You must have used or implemented the hash tables or dictionaries, in whichever language you code.
So, in a hash table, for searching, the time taken is generally O(1), or constant time. However, there are situations when it takes O(N) times because it has to execute that many operations to search for a value.
Similarly, when we try to insert some value in a hash table, for a majority of the cases it takes a time of O(1), but still, there are cases when suppose multiple collisions occur, when it takes a time of O(N), for the collisions resolution.
Other data structures we need amortized analysis are Disjoint Sets etc.
How frequently do we use the amortized case analysis of any algorithm ?
Whenever a single operation or very few operations runs slowly on occasion, but most of the operations run quickly and frequently, then the amortized case analysis is used.
Recursive Complexity
In computer science, when a function (or method or subroutine) calls itself, we call it recursion.
To find out the recursive complexities of the algorithms, we perform the below steps :
- Step – 1 :
Determine the number of subproblems and the parameters indicating the size of each subproblem’s input (function call with smaller input size). For example, for finding the NthNth Fibonacci number, the number of subproblems is 2, and the input size of subproblems are (N−1) and (N−2). - Step – 2 :
Add the time complexities of the sub-problems with the total number of fundamental operations performed at that particular stage of recursion. - Step – 3 :
Create a recurrence relation for the number of times the operation is done, with the proper base condition. For example, the recurrence relation for finding out the Nth Fibonacci number is T(N)=T(N−1)+T(N−2)+c. - Step – 4 :
Find a solution to the recurrence, or at the very least, determine how it will develop. There are many ways to analyze the recurrence relation, however, the two most popular methods for finding the solutions for the recurrence relations are Master Theorem and Recursion Tree Method.
Note :
A recurrence relation is an equation that defines a sequence based on some condition that gives the next term as a function of the previous terms.
Recursion Tree Method
In a recurrence tree, each node refers to the cost of a specific recurrent subproblem. We add up all of the node values to determine the algorithm’s overall complexity.
Steps for solving a recurrence relation :
- Firstly determine the recurrence relation and draw a recursion tree on its basis.
- Next, calculate the number of levels, and the cost at each level, including the cost at the last level.
- Finally, add up the costs of all the levels to further simplify the expression.
Suppose, we want to solve the below recurrence relation by the recurrence Tree method :
T(N) = 2*T(N/2) + CN
Now we can conclude the below points from the above recurrence relation :
- The original problem of size NN is divided into two sub-problems of the size = N/2N/2.
- Next, the overall cost of dividing the subproblem and combining its solution, for size = NN, is CNCN, where CC is a constant.
- The problem is divided into half every time until the size of the problem reduces to 1.
- Below is the recursion tree for the problem, which is based on the recurrence relation :
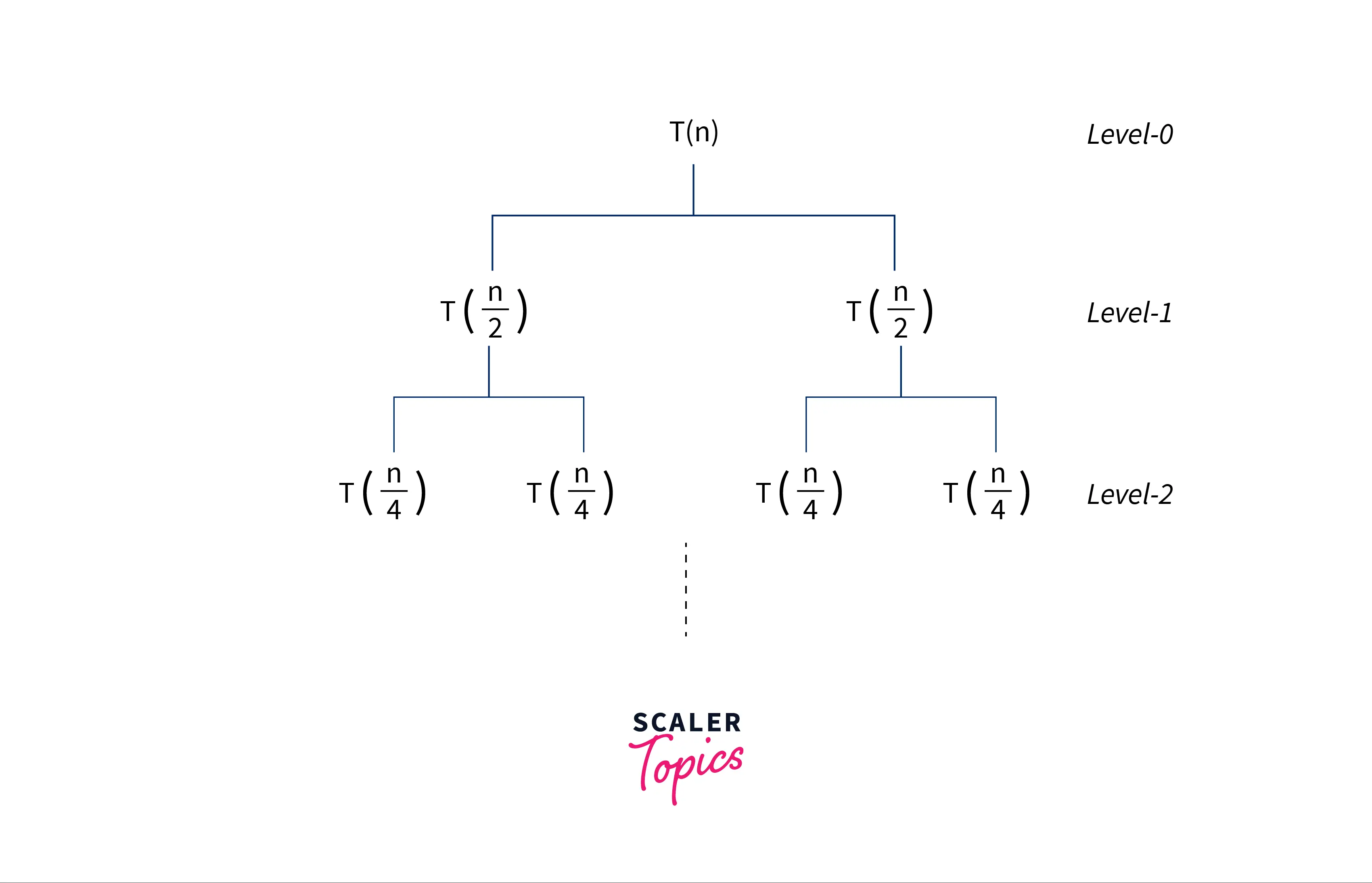
Cost at each level :
Suppose, the cost for dividing and then combining the solutions for size $N/2^k$ is equal to $N/2^k$.
Number of nodes at each level = $2^k$.
Hence, the cost at each level will be computed as below :
$(N/2^k)*(N^k) = N$
Number of Levels :
As you can see from the recursive diagram, the number of levels in the recursion tree is $log2(N)$. Because at each level the number of subproblems gets divided by a factor of 2.
Cost at the last level
At the last level, the size of the problem is 1 and the number of subproblems is N.So, cost = $N*T(1)$ = $O(N)$
After adding up the cost at each level :
cost = { N + N + N + ..logN times } + O(N)
=> cost = O(NlogN) + O(N)
=> Overall time complexity = O(NlogN)Hence, the time complexity of the above recurrence relation is $O(N logN)$.
Code Complexity
We have already learned about the code complexity of the recursive solutions. Now, we will look at some iterative and non-iterative codes and try to determine their complexity.
Constant Operations
The constant operations such as arithmetic, boolean, and logical operations take a constant running time. The space taken by them is also constant.
Look at the below examples for understanding better :
Code :
int a = 10 + b;
int k = a*5
Time Complexity :
Time complexity is O(1) Because, there are no iterations or loops involved in this process. There is just a constant operation performed.
Space Complexity :
Space complexity is O(1) because we are not using any additional data structure to store our results. We are simply using variables, which take constant space in memory.
If-Else Operations
The If-Else operations also take a constant running time. Also, the space taken by them is constant.
Look at the below examples for understanding better :
Code :
if( n> 100)
{
a = a + 10;
}
else {
a = a + 5;
}
Time Complexity :
Time complexity is O(1) because, there are no iterations or loops involved in this process. There are just constant if-else operations performed.
Space Complexity :
Space complexity is O(1) because we are not using any additional data structure to store our results. We are simply using variables, which take constant space in memory.
for / while Loops
The for/While Loops operations take the time complexity which is proportional to the size of the input and how many times the loop will execute. Also, the space taken by them is either constant or in terms of the space taken by the data structure(say array) to hold the values of the operations performed under the loops.
Look at the below examples for understanding better :
Code :
for(int i=0;i<n;i++)
{
a = a + i;
}Time Complexity :
The time taken for the code will be $O(n)$ because the loop will run for $n$ times.
Space Complexity :
Space complexity is $O(1)$ because we are not using any additional data structure to store our results. We are simply using variables, which take constant space in memory.
Nested for / while Loops
The nested for/While Loops operations take the time complexity which is proportional to the size of the input and how many times the loop is nested. For example, for an input of size $N$, if we have two nested loops then the time taken will be $O(N^2)$, for three nested loops the time taken will be $O(N^3)$, etc.
Also, the space taken by them is either constant or in terms of the space taken by the data structure(say array) to hold the values of the operations performed under the loops.
Look at the below examples for understanding better :
Code :
for(int i=0;i<n;i++)
{
for(int j=0;i<n;i++){
x = x*j
}
}Time Complexity :
The time taken for the code will be $O(n^2)$ because the inner loop will run for $n$ times, for every execution of the outer loop. And the outer loop itself will run for $n$ times.
Space Complexity :
Space complexity is $O(1)$ because we are not using any additional data structure to store our results. We are simply using variables, which take constant space in memory.
Conclusion
In this article, we learned about the analysis of the algorithms. Let us get a quick recap of what we learned throughout.
- By analyzing an algorithm, we get an idea of how the algorithm will scale with the variation (change) in the input size.
- Analysis of algorithm is also used to compare various algorithms for solving the same problem.
- There are three types of analysis of algorithms. They are the Best case, Average case, and Worst case.
- Best case analysis of algorithms gives us the lower bound on the running time of the algorithm.
- The worst-case analysis of algorithms gives us the upper bound on the running time of the algorithm
- The average case analysis of algorithms takes the sum of the running time on every possible input, and after that, it takes the average.
- The amortized analysis deals with the overall cost of the operations.
- There are various ways to calculate the recursive complexities and normal code complexities, and we discussed them in depth.