1-D Dynamic Programming Problem

1 dimensional dynamic programming(DP) problems are problems that can be solved with the use of DP on a 1-D (1-dimensional) array.

Scope of Article

• This article discusses the basic definition of dynamic programming, followed by the approach to solve DP problems in data structures.
• It includes two examples of 1-D DP problems – fibonacci and counting stairs along with their code in cpp (solved using DP)

Takeaways

Approach to solving 1-D DP problems:

• Using memoization
• Using tabular method

What is a 1-D Dynamic Programming Problem?

Before we move to discussing a 1D dp problem, let’s define dp -- dynamic programming. Dynamic programming (DP) is a technique used by programmers to solve problems wherein the problems are broken down to smaller sub problems (that have the same nature as that of the main problem) which are solved just once, and the results of the computation are saved for the future so that we need not compute the saved results again. Why can we not compute them again? If we can save the results of computations that are recurring, then that way we are saving time.

So we can say that dynamic programming is a technique that can be used to optimize the time complexity of a solution. Dynamic programming problems are based on recursion and are the optimizations of recursion.

Let’s take an example of the Fibonacci series and understand how. In this series we start with the number 1 and 1. The next number is the sum of the previous two numbers. Hence the next number would be 2 (1 + 1) and the next would be 3 (2 + 1). The series would look like – 0, 1, 1 2, 3, 5, 8, 13, ... and so on i.e.

fibonacci(0) = 0
fibonacci(1) = 1
fibonacci(2) = 1
fibonacci(3) = 2

So how are we going to find fibonacci(n)? We can say that it is fibonacci(n - 1) + fibonacci(n - 2), and this is essentially it’s recursive solution. If you’re not clear with recursion, take some time to revise it well before moving on to dynamic programming.

The recursive code would look like this:

int fibonacci(n){
    if (n < 2)
        return n;
    return fibonacci(n - 1) + fibonacci(n - 2);
}

Let’s try to find out fibonacci(5). Since 5 > 2, fibonacci(5) = fibonacci(5 - 1) + fibonacci(5 - 2) i.e. fibonacci(4) + fibonacci(3).

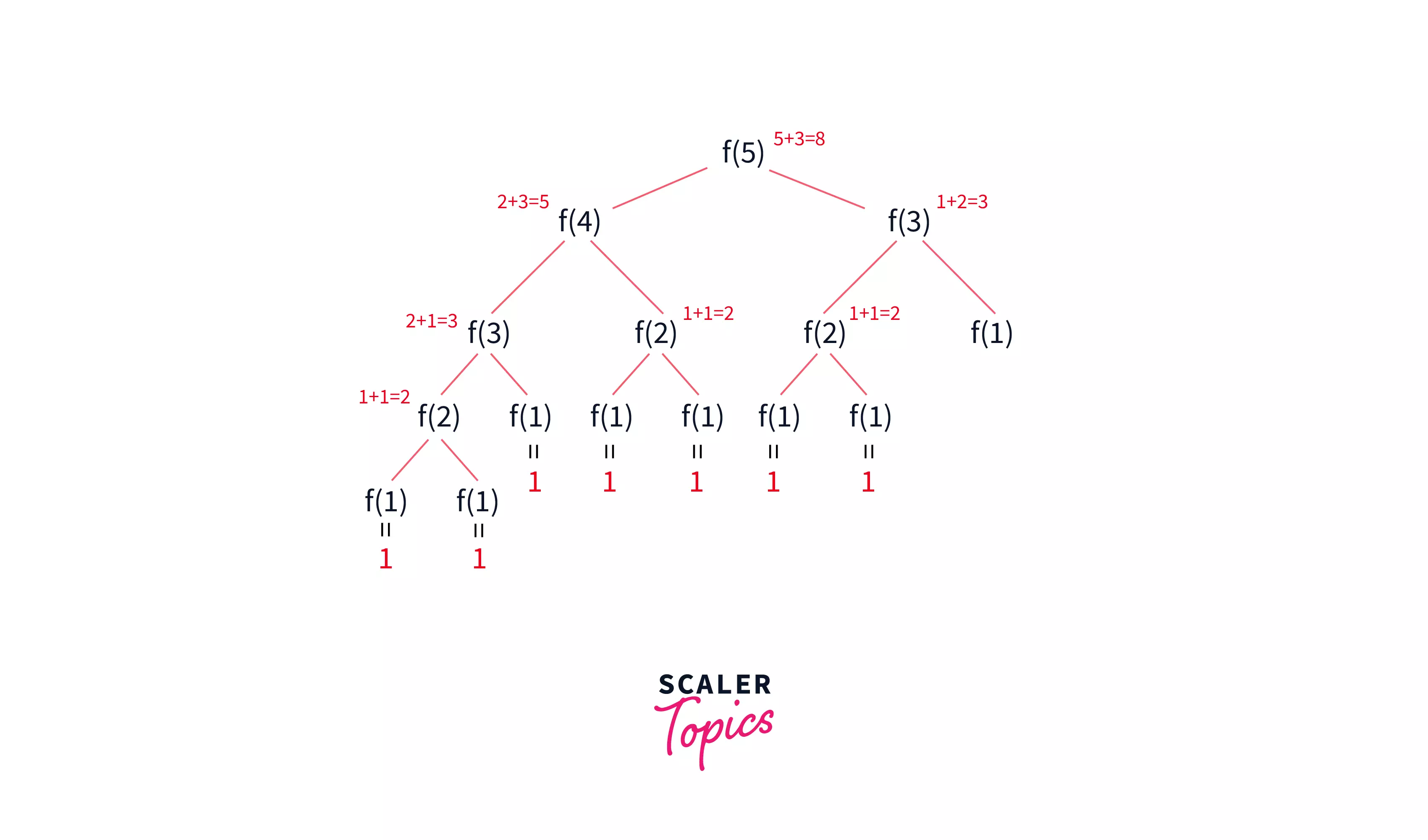
As we can see in the diagram above, fibonacci(5) calls fibonacci(4) and fibonacci(3). In turn, fibonacci(4) calls fibonacci(2) and fibonacci(3) and fibonacci(3) calls fibonacci(2) and fibonacci(1). Do you see the number of times that fibonacci 3, 2 and 1 are called? Everytime that fibonacci(2) is called, it computes it. What we studied just a while ago, was that dynamic programming is all about reducing the number of computations and so our goal would be to not compute the value of fibonacci(2), fibonacci(3) and 1 multiple times.

What are we going to do to reduce these computations? We will save these values so that we don’t have to compute them again and again. This example was of a small number, however if you were to calculate fibonacci(245), how many times would you compute the fibonacci of the smaller numbers such as 2, 3, 4, 5, 6 and so on?

Dynamic programming would help us solve this problem. We would store the results of these smaller computations so as to make our solution optimal.

Approach to solving DP problems (1-D Problems Specifically)

Now that we know what DP is, we can start solving problems. Let’s look at the approach to solve DP problems —

Using memoization:

1. Identify that the problem is a DP problem:
   The first step to solving a dynamic programming problem is to identify it. How would you do that? Generally, any problem that requires you to maximize or minimize a certain quantity, or perhaps problems in which you are required to count arrangements in certain conditions or even problems that involve probabilities are problems that can be solved with the use of Dynamic Programming.
   All the problms that can be broken down to smaller subproblems that overlap(such as the computation of fibonacci) of certain numbersin the example above) can be solved with dynamic programming.
2. Write the recursive code:
   As we read above, DP problems are an optimization of the recursive problems. And so, if you write the recursive code of the problem, you will be able to write the DP code for the problem.
3. Memoization:
   Memoization is the technique of storing the results of previous computations as we discussed earlier. To solve a 1 Dimensional (1D) DP problem, we make use of an array to store these results.

Using tabular method:

To solve DP problems using the tabular method, we just have 1 step extra post the memoization, wherein we make no calls to the function at all, and all values are stored and retrieved from the 1-D array we created. You’ll see the difference in a while.

Once you’re done with these 3 or 4 steps depending on the method, you can simply return the n^th term in your DP array.

Example 1: Fibonacci Series With Code

Now let’s apply these steps to solve a 1 dimensional dynamic programming problem — the fibonacci series tha we discussed earlier.

The first step is identification. Scroll up and take a look at the chart where we calculated fibonacci(5). We can see that there are multiple overlapping sub problems, we are calculating the value of fibonacci(1), fibonacci(2) and fibonacci(3) multiple times. Hence, we can say that it is a DP problem.

The next step — writing the recursive code. We have already written the recursive code for this problem:

int fibonacci(int n){
    if (n < 2)
        return n;
    return fibonacci(n - 1) + fibonacci(n - 2);
}

Now comes the most important step, that is memoization where we essentially store the values that we compute. So here, we will store the values of every fibonacci number in an array starting with fibonacci(0) and fibonacci(1) since they are the base cases. Post that, we will compute fibonacci(2), fibonacci(3) and so on, and simultaneously save these results and use them for future calculations.

Here’s how we would do it:

• Create an array, dp, of size n — where n is the n^th fibonacci term that you want to find
• Set dp[0] and dp[1] to 1 as the 0th fibonacci is 0 and 1st fibonacci term is 1
• Run a loop from i = 2 to n (since dp[0] and dp[1] are already set to 1) to compute the i^th fibonacci term by calling fib(n – 1) + fib(n – 2) since fibonacci series is the addition of 2 previous terms
• Return dp[n]

int fib_term[1000];

int fibonacci(int n){
    if (n <= 1){
        return n;
    }

    // if the value of fib_term(n) has already been calculated, it's value in the array will not be 0, and if it isn't we can return fib_term(n)
    if (fib_term[n] != 0)
        return fib_term[n];

    // calculating fib_term(n)
    else {
        fib_term[n] = fibonacci(n - 1) + fibonacci(n - 2);
        return fib_term[n];
    }
}

The above solution was our memoization solution. Let’s take it one step further and write the tabular method solution for the problem. If we are storing the values of fibonacci terms that we have calculated, we can further reduce calling the fibonacci() function in line 14 by simply getting the values of fibonacci(n - 1) and fibonacci(n - 2) which were previously computed from the array as fib_term[n - 1] and fib_term[n - 2].

In the following code, we’ve created the array (dp array) of size n (size of our problem) and stored values in it.

int fibonacci(int n){
    int dp[n];
    dp[0] = 0;
    dp[1] = 1;
    for (int i = 2; i <= n; i++){
        dp[i] = dp[i - 1] + dp[i - 2];
    }
    return dp[n];
}

And it’s as simple as that! Let’s take another example to perfect your understanding.

Example 2: N-Stairs Problem

The N-stairs problem is another classic DP problem. Here’s the problem statement:

You have n stairs, and you’re standing at the bottom and want to reach the top of the staircase. Count the number of ways you can climb the stairs if you can only climb either 1 step / stair or 2 steps at one time.

Scroll up and see the first step to solving a DP problem — identifying it. We read that a problem that requires you to count arrangements with certain conditions can be classified as a DP problem, and this, is just that!

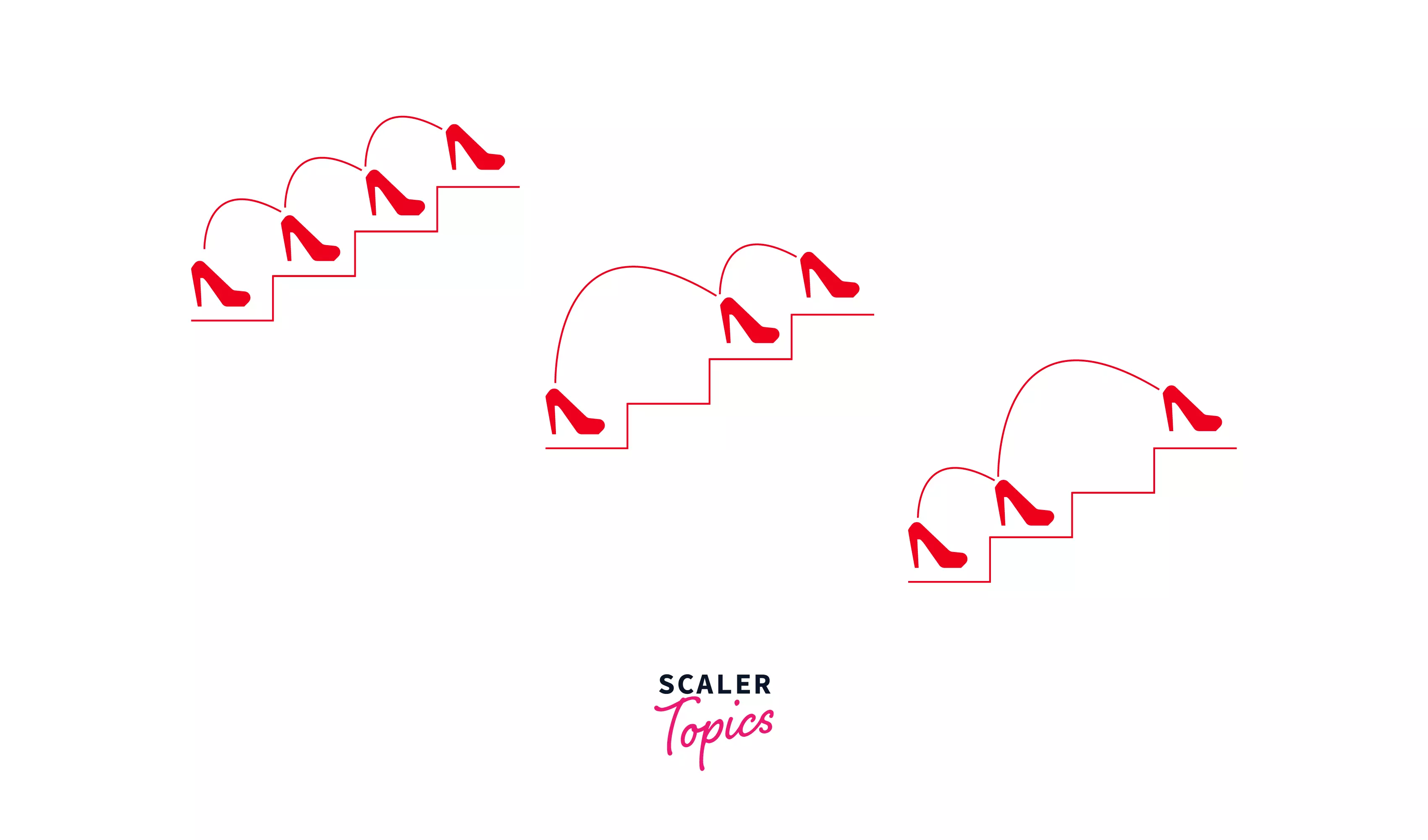
Take a look at this example of the problem in the figure. We have 3 steps as you can see and initially, we’re standing at the bottom. Now one way to reach the top is to take 3 steps one by one, another way would be to take two initially, and then 1 step. Finally, we could take 1 step and then 2 to reach the top.We have identified that this is a DP problem, and now we need to write the recursive code. To write recursive code, there are 2 main elements – base condition, and recursive function call.

Let’s make some observations. What are the ways to reach the last step, or any n^th step? You can reach the n^th step from the (n – 1)^th step or the (n – 2)^th step. So, if we find out the number of ways we can reach the (n – 1)^th step and the (n – 2)^th step, then we can add them to find out the number of ways to reach the n^th step. You have successfully figured out the recursive call.

If you look at it, this is how it is:

ways(n) = ways(n - 1) + ways(n - 2)

This statement looks pretty familiar. You’re right, this is just like the fibonacci series. However, there’s one difference:

ways(1) = 1 = fibonacci(2)

ways(2) = 2 = fibonacci(3)

ways(3) = 3 = fibonacci(4)

The number of ways to reach the n^th step is equal to n + 1^th fibonacci number.

So if we need to find ways to reach the n^th stair, we can simply return n + 1^th fibonacci number.

int fibonacci(int n){
    if (n < 2)
        return n;
    return fibonacci(n - 1) + fibonacci(n - 2);
}

int ways(int n){
    return fibonacci(n + 1);
}

That looks correct, but we now need to find the 1D DP solution of this problem. Again, simple, we’ll memoize the fibonacci solution the way we did in the previous solution, and return ways(n) as fibonacci(n + 1).

So our memoized solution to the counting stairs problem would look like this in cpp:

int fib_term[1000];

int fibonacci(int n){
    if (n <= 1){
        return n;
    }

    // if the value of fib_term(n) has already been calculated, it's value in the array will not be 0, and if it isn't we can return fib_term(n)
    if (fib_term[n] != 0)
        return fib_term[n];

    // calculating fib_term(n)
    else {
        fib_term[n] = fibonacci(n - 1) + fibonacci(n - 2);
        return fib_term[n];
    }
}

int ways_to_reach_stair(int n){
    return fibonacci(n + 1);
}

Now again, we can improve this by tabulating our results the following way:

int fibonacci(int n){
    int dp[n];
    dp[0] = 0;
    dp[1] = 1;
    for (int i = 2; i <= n; i++){
        dp[i] = dp[i - 1] + dp[i - 2];
    }
    return dp[n];
}

int ways_to_reach_stair(int n){
    return fibonacci(n + 1);
}

You can now follow the steps above to solve any 1 dimensional DP problem!

Time and Space Complexity

To calculate the time complexity of the DP solution, take a look at the final code (tabulated). We have a for loop running from i = 2 to n. And to store the values of the computed numbers, we use an array of size n making the space complexity linear as well. Hence the time and space complexities for both the problems discussed above are linear – O(n).

For most 1 dimensional DP problems, the solution would be similar. For the essence of dynamic programming, you would store the previously computed values in a table, and you would run a loop to fill in the values into the table making the time and space complexity of 1D DP linear.

Conclusion

• Dynamic programming is a technique that is used to optimize the time complexity of a solution by tabulating and storing results of previous computations.
• Approach to solving 1-DDP problems:
  • Identify the problem statement as a DP problem
  • Write the recursive code
  • Memoization
  • Tabulation
• Time and space complexities of 1 dimensional DP problems are usually linear.